Solución Problema 2 de la Ley de Hooke

En este segundo ejercicio resuelto, nuevamente vamos a reforzar los conocimientos adquiridos en el tema de La ley de Hooke en el área de Elasticidad, con este ejemplo resuelto, el alumno podrá corroborar su respuesta y verificar si ha llegado al mismo resultado. ??

Nivel de Dificultad: ⭐⭐

Solución:

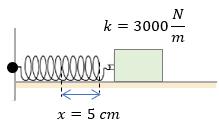
En este ejemplo de la ley de hooke vemos claro como la masa que está sujeta al resorte está en posición horizontal, es decir que no tenemos porque involucrar a la gravedad para obtener la fuerza necesaria para comprimir 5 centímetros, esto es algo totalmente relevante porque podemos diferenciar los dos tipos de problemas, cuando el resorte está vertical y cuando está horizontal, entonces su solución es muy más simple.

• Cálculo de la fuerza necesaria para comprimir cierta distancia

Datos:

$latex \displaystyle k=3000\frac{N}{m}$

$latex \displaystyle x=5cm$

a) Calculando la fuerza

Con el simple hecho de analizar la fórmula, sabemos que nuestros datos tenemos que ponerlos en la fórmula y listo. Pero antes de poder realizar el cálculo, es necesario que las unidades de distancia estén en el Sistema Internacional por lo cual, realizaremos la conversión:

$latex \displaystyle x=5cm\left( \frac{1m}{100cm} \right)=0.05m$

Ahora si podemos sustituir en la fórmula de la ley de hooke

$latex \displaystyle F=kx=\left( 3000\frac{N}{m} \right)\left( 0.05m \right)=150N$

Es decir que la fuerza necesaria tiene que ser de 150 Newtons.

Resultado:

$latex \displaystyle F=150N$