Integrales por Sustitución Trigonométrica
Aprende a resolver paso a paso integrales por Sustitución Trigonométrica
Uno de los métodos de integración que más nos pidieron nuestros lectores, fue este método, el método de integración por sustitución trigonométrica, este tipo de integrales en las que aparece las formas
Es muy importante mencionar que este tipo de integrales, no necesarimente se pueden resolver aplicando una sustitución trigonométrica, hay formas para realizar las integrales aplicando otro método en algunos casos, pero aquí explicaremos puramente los de sustitución trigonométrica.
Pasos Para Realizar las Integrales Por Sustitución Trigonométrica
Vamos a explicar brevemente, como realizar los pasos correctamente para entender la finalidad de este método de integración. Lo primero que debemos entender, es ¿cómo es la integral que vamos a resolver? ¿a qué tipo de integral se parece?, observa la tabla y verifica el cambio trigonométrico que se sugiere:
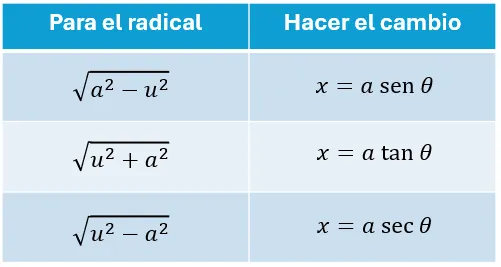
Paso 1:
Lo primero que debemos de realizar, es el cambio de variable que corresponde conforme al radical que aparezca y efectuar las operaciones algebraicas que sean necesarias para que desaparezca el radical, con lo cual la integral original se transforma en una integral trigonométrica.
Paso 2:
Realizar la integral trigonométrica que resultó en el paso anterior, si hay que simplificar se simplifica a lo máximo y se ocupan las identidades trigonométricas más comunes:

Paso 3:
Regresar a la variable original, para lo cual debemos de tener en cuenta:
- a) Se despeja la variable en función del ángulo usado en el cambio de variable.
- b) Se dibuja un triángulo rectángulo que represente la relación trigonométrica elegida y se calcula el lado faltante con el Teorema de Pitágoras. Ese lado siempre será la raíz cuadrada original. A partir de ahí, se encuentran los valores de las demás funciones trigonométricas usadas en la integral.
- c) Se reemplazan esas funciones trigonométricas en el resultado obtenido en el paso anterior.
Como siempre mencionamos en el blog, no hay mejor forma que realizar ejercicios para entenderlo mucho mejor:
Ejercicios Resueltos de Integrales por Sustitución Trigonométrica
Solución:
Realizamos la sustitución trigonométrica:
Derivamos ambos lados:
Sustituyendo en la integral:
Simplificamos la raíz:
Sustituyendo en la integral:
Cancelamos
Integrando:
Dado que
Podemos guiarnos también, a través del triángulo:
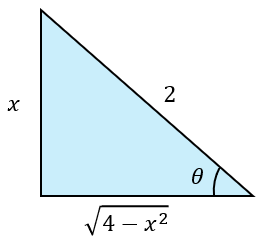
Por lo tanto, el resultado es:
¿Tuviste problemas para entender la integral?, no te preocupes mira el video paso a paso 👇
| 🎵 Ver en TikTok | 📷 Ver en Instagram |
Solución:
Realizamos la sustitución trigonométrica:
Derivamos ambos lados:
Sustituyendo en la integral:
Simplificamos la raíz:
Sustituyendo en la integral:
Cancelamos
La integral de
Aplicando el triángulo:
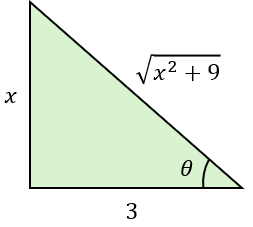
Como
Sustituyendo en la solución:
Factorizamos
Finalmente, el resultado es:
¿Tuviste problemas para entender la integral?, no te preocupes mira el video paso a paso 👇
| 🎵 Ver en TikTok | 📷 Ver en Instagram |
Solución:
Realizamos la sustitución trigonométrica:
Derivamos ambos lados:
Sustituyendo en la integral:
Simplificamos la raíz:
Sustituyendo en la integral:
Cancelamos
Sacamos la constante:
La integral de
Podemos guiarnos del triángulo:
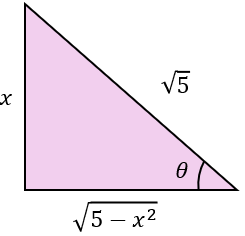
Dado que
Sustituyendo en la solución:
Cancelamos
Finalmente, el resultado es:
¿Tuviste problemas para entender la integral?, no te preocupes mira el video paso a paso 👇
| 🎵 Ver en TikTok | 📷 Ver en Instagram |
Solución:
Reescribimos la integral en una forma más conveniente:
Usamos la sustitución trigonométrica:
Derivamos ambos lados:
Sustituyendo en la integral:
Utilizamos la identidad
Simplificamos la potencia:
Sabemos que:
La integral de
Como
Podemos guiarnos con el triángulo:
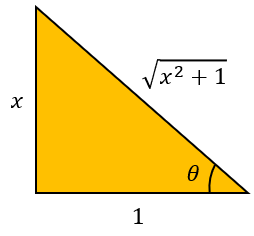
Sustituyendo en la solución:
Finalmente, el resultado es:
¿Tuviste problemas para entender la integral?, no te preocupes mira el video paso a paso 👇
| 🎵 Ver en TikTok | 📷 Ver en Instagram |
Solución:
Usamos la sustitución trigonométrica:
Derivamos ambos lados:
Sustituyendo en la integral:
Simplificamos la raíz:
Sustituyendo en la integral:
Usamos la identidad:
Sustituyendo:
Distribuimos:
La integral de
Expresamos en términos de
Sabemos que:
Por el triángulo tenemos que:
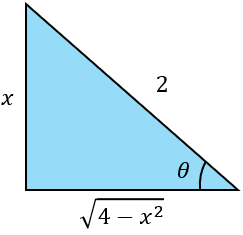
Por lo que:
También sabemos que:
Sustituyendo en la solución:
Finalmente, el resultado es:
¿Tuviste problemas para entender la integral?, no te preocupes mira el video paso a paso 👇
| 🎵 Ver en TikTok | 📷 Ver en Instagram |
Solución
Usamos la sustitución trigonométrica:
Derivamos ambos lados:
Sustituyendo en la integral:
Simplificamos la raíz:
Por lo que:
Sustituyendo en la integral:
Cancelamos términos:
Usamos la identidad:
Sustituyendo:
Sabemos que:
Por lo que:
Expresamos en términos de
Sabemos que:
Aplicando el triángulo:
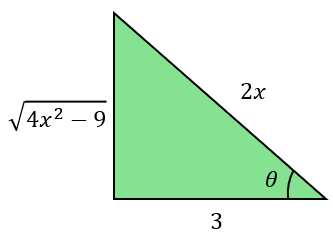
Por lo que:
También sabemos que:
Sustituyendo en la solución:
Finalmente, el resultado es:
¿Tuviste problemas para entender la integral?, no te preocupes mira el video paso a paso 👇
| 🎵 Ver en TikTok | 📷 Ver en Instagram |
Deja una respuesta

Estos temas te pueden interesar