Ley de Gauss - Ejercicios Resueltos

¿Alguna vez has imaginado medir un campo eléctrico sin seguir líneas de fuerza? La Ley de Gauss es la herramienta perfecta cuando las condiciones lo permiten: permite calcular campos eléctricos sin usar directamente la Ley de Coulomb, y se vuelve esencial en distribuciones con simetría.

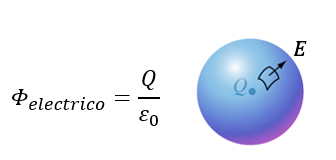
En este artículo abordaremos la Ley de Gauss de forma teórica y práctica, con algunos ejercicios resueltos como lo hacemos en Fisimat.

¿Qué nos dice la Ley de Gauss?

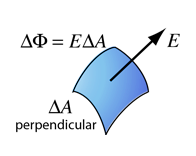
La Ley de Gauss establece que el flujo eléctrico total a través de una superficie cerrada es igual a la carga neta encerrada dividida entre la permitividad del vacío, La Ley de Gauss es un pilar fundamental del electromagnetismo que relaciona el flujo eléctrico a través de una superficie cerrada (llamada superficie gaussiana) con la carga neta encerrada en su interior.

\[
\Phi_E = \oint_S \vec{E} \cdot d\vec{A} = \frac{q_{\text{int}}}{\varepsilon_0}
\]

Donde:

\( \Phi_E \) : flujo eléctrico total
\( \vec{E} \) : campo eléctrico
\( d\vec{A} \) : vector diferencial de área
\( q_{\text{int}} \) : carga encerrada
\( \varepsilon_0 \approx 8.85 \times 10^{-12} \, \text{C}^2/\text{N·m}^2 \) : permitividad del vacío

¿Cuándo es útil la Ley de Gauss?

Esta ley es especialmente útil cuando existe simetría

Esférica: cargas puntuales, esferas cargadas

Cilíndrica: hilos largos, tubos cargados

Plana: placas infinitas

El flujo neto depende únicamente de la carga interna, incluso si hay cargas externas cerca. Estas últimsa contribuyen con flujos entrantes y salientes que se cancelan, sin alterar la carga encerrada.

Nota: No es recomendable cuando la distribución de carga es irregular o carece de simetría.

Ejercicios Resueltos de la Ley de Gauss

Campo eléctrico de una carga puntual

Solución:

1. Se elige una superficie esférica de radio \( r \).
2. Por simetría, el campo eléctrico \( \vec{E} \) es constante en la superficie.
3. Flujo:
\[
\Phi_E = E \cdot 4\pi r^2
\]4. Aplicamos la Ley de Gauss:
\[
E \cdot 4\pi r^2 = \frac{q}{\varepsilon_0}
\Rightarrow E = \frac{1}{4\pi \varepsilon_0} \cdot \frac{q}{r^2}
\]

Este resultado coincide con la Ley de Coulomb.

Campo eléctrico de un hilo cargado infinitamente largo

Solución:

1. Elegimos una superficie cilíndrica coaxial de radio \( r \) y longitud \( L \).
2. Flujo:
\[
\Phi_E = E \cdot (2\pi r L)
\]3. Carga encerrada:
\[
q_{\text{int}} = \lambda L
\]4. Aplicamos la Ley de Gauss:
\[
E \cdot (2\pi r L) = \frac{\lambda L}{\varepsilon_0}
\Rightarrow E = \frac{\lambda}{2\pi \varepsilon_0 r}
\]

Campo eléctrico de una esfera uniformemente cargada

a) Dentro de la esfera (\( r < R \))
b) Fuera de la esfera (\( r > R \))

Solución:

a) Para \( r < R \):}

Volumen encerrado:
\[
V = \frac{4}{3}\pi r^3
\]Carga encerrada:
\[
q_{\text{int}} = \rho \cdot V = \rho \cdot \frac{4}{3}\pi r^3
\]Flujo:
\[
\Phi_E = E \cdot 4\pi r^2
\]Aplicamos la ley:
\[
E \cdot 4\pi r^2 = \frac{\rho \cdot \frac{4}{3}\pi r^3}{\varepsilon_0}
\Rightarrow E = \frac{\rho r}{3\varepsilon_0}
\]

b) Para \( r > R \):}

Carga total encerrada:
\[
q = \rho \cdot \frac{4}{3}\pi R^3
\]Aplicamos la ley:
\[
E \cdot 4\pi r^2 = \frac{q}{\varepsilon_0}
\Rightarrow E = \frac{1}{4\pi \varepsilon_0} \cdot \frac{q}{r^2}
\]

Campo eléctrico de una lámina plana infinita

Solución:

1. Superficie tipo “pastilla” (dos caras planas).
2. Carga encerrada:
\[
q_{\text{int}} = \sigma A
\]3. Flujo total (dos lados):
\[
\Phi_E = 2EA
\]4. Aplicamos la Ley de Gauss:
\[
2EA = \frac{\sigma A}{\varepsilon_0}
\Rightarrow E = \frac{\sigma}{2\varepsilon_0}
\]

El campo es constante y perpendicular a la superficie.

Conclusión

La Ley de Gauss permite resolver problemas complejos de campo eléctrico de forma simple y elegante, siempre que haya simetría. Dominar sus aplicaciones te ahorra tiempo y fortalece tu visión matemática del electromagnetismo.