Choques Elásticos e Inelásticos - Ejercicios Resueltos
¿Qué tal amigos de Fisimat?, hoy vamos a comenzar con un artículo interesante en Física, los choques elásticos e inelásticos. ¿pero qué importancia o relevancia tienen este tipo de temas dentro de la física?, ¿por qué es importante aprenderlo?, pues bien. Empecemos con lo siguiente:
Imagina que dos automóviles chocan en un cruce, ¿qué sucede después del impacto? ¿conservan su velocidad inicial o pierden energía? Estas situaciones cotidianas ilustran dos conceptos claves dentro de la física: los choques elásticos e inelásticos. En este post vamos explorar las diferencias, las fórmulas que rigen este tema, y resolveremos ejercicios prácticos para ayudarte a entenderlos mejor.
¿Qué son los choques?
Un choque es el encuentro entre dos cuerpos cuando al menos uno de ellos lleva una cierta velocidad. Durante este evento, ocurre una interacción en la que los cuerpos, debido a su masa y velocidad, ejercen fuerzas impulsivas entre sí. Estas fuerzas son de corta duración pero lo suficientemente intensas como para generar cambios en las velocidades de los cuerpos involucrados.
En un choque, todos los cuerpos experimentan una ligera deformación. En algunos casos, esta deformación es temporal y los cuerpos recuperan su forma original, mientras que en otros, la deformación es permanente. Además, durante el impacto, parte de la energía del sistema puede liberarse en forma de calor o sonido.
Desde el punto de vista físico, los choques son eventos en los que rigen dos principios fundamentales:
- La conservación del momento lineal, que siempre se cumple independientemente del tipo de choque.
- La energía cinética, que puede conservarse o transformarse en otras formas de energía según la naturaleza del choque.
De acuerdo con la elasticidad o capacidad de restitución de los cuerpos, un choque puede ser clasificado como elástico o inelástico.
¿Choques elásticos e inelásticos?
Choques elásticos
Un choque es completamente elástico cuando se conserva la energía cinética. Lo que significa que de manera ideal no se pierde ninguna energía en forma de calor, ya que no hay ninguna deformación durante el choque. Tal es el caso de los choques entre átomos y moléculas de un gas, además de conservarse el momento lineal, esto significa que no hay pérdida de energía mecánica en el sistema durante el impacto.
Ejemplo: el choque entre bolas de billar, donde las bolas rebotan sin deformarse de manera permanente ni generar calor significativo.
Choques inelásticos
Por otro lado, en un choque inelástico, aunque el momento lineal se conserva, parte de la energía cinética inicial se transforma en otras formas de energía, como calor, sonido, o energía de deformación. En el caso extremo, llamado choque perfectamente inelástico, los cuerpos quedan unidos después del impacto y comparten una velocidad común.
Ejemplo: una colisión frontal entre dos automóviles que se deforman y quedan enganchados tras el impacto.
Tabla comparativa entre choques elásticos e inelásticos
| Aspecto | Choque elástico | Choque inelástico |
|---|---|---|
| Conservación de momento | Sí | Sí |
| Conservación de energía cinética | Sí | No |
| Transformación de energía | Ninguna | En calor, sonido o deformación |
| Ejemplo | Bolas de billar | Colisión de automóviles |
Ley de la conservación de la Cantidad de Movimiento o del Momento Lineal
La ley de la conservación de la cantidad de movimiento señala lo siguiente: cuando dos o más cuerpos chocan la cantidad de movimiento es igual antes y después del choque. Esto significa que si dos o más cuerpos chocan, el resultado de la suma vectorial correspondiente a las cantidades de movimiento de los cuerpos después del choque es igual a la suma de los vectores que corresponde a las cantidades de movimiento de los cuerpos antes de él.
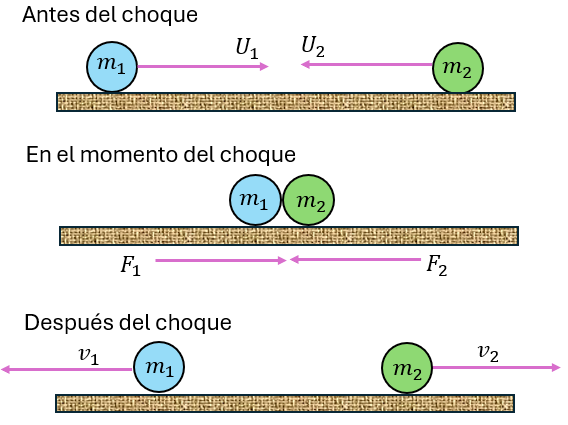
Efectuemos el análiss del choque de frente de dos esferas de acero cuyas masas son m1 y m2 , representando $\displaystyle {{U}_{1}}$ y $\displaystyle {{U}_{2}}$ las velocidades que llevan antes del choque, y por $\displaystyle {{v}_{1}}$ y $\displaystyle {{v}_{2}}$ las velocidades que llevan después del mismo, tal como se ilustra en la imagen siguiente:
Antes del choque, tanto la masa 1 como la masa 2 tienen una cantidad de movimiento igual al producto de su masa por su velocidad, de manera que la cantidad de movimiento total antes del choque es:
$\displaystyle {{m}_{1}}{{U}_{1}}+{{m}_{2}}{{U}_{2}}$ (1)
En el momento del choque la masa 2 recibe un impulso debido a la fuerza 1 cuya magnitud es:
$\displaystyle {{F}_{1}}t={{m}_{2}}{{v}_{2}}-{{m}_{2}}{{U}_{2}}$ (2)
La masa 1 también recibe un impuslo causado por la fuerza 2 cuya magnitud es:
$\displaystyle {{F}_{2}}t={{m}_{1}}{{v}_{1}}-{{m}_{1}}{{U}_{1}}$ (3)
Al considerar positivo el impuslo de la fuerza (por ser hacia la derecha) y negativo el de la fuerza 2 (por ser hacia la izquierda), tenemos que en el momento del choque:
$\displaystyle {{F}_{1}}t=-{{F}_{2}}t$ (4)
Sustituyendo estas expresiones por el cambio en la cantidad de movimiento a que dan origen (ecuaciones 2 y 3) tenemos:
$\displaystyle {{m}_{1}}{{v}_{1}}-{{m}_{1}}{{U}_{1}}=-\left( {{{m}_{2}}{{v}_{2}}-{{m}_{2}}{{U}_{2}}} \right)$ (5)
Reagrupando términos:
$\displaystyle {{m}_{1}}{{U}_{1}}+{{m}_{2}}{{U}_{2}}=\left( {{{m}_{1}}{{v}_{1}}+{{m}_{2}}{{v}_{2}}} \right)$ (6)
Dónde:
$\displaystyle {{m}_{1}}{{U}_{1}}+{{m}_{2}}{{U}_{2}}$ = Cantidad de movimiento antes del choque
$\displaystyle {{{m}_{1}}{{v}_{1}}+{{m}_{2}}{{v}_{2}}}$ = Cantidad de movimiento después del choque
La ecuación (6) nos señala claramente la ley de la conservación de la cantidad de movimiento y después de la cantidad de movimiento es la misma.
Ejercicios Resueltos de Choque elástico e Inelástico
Solución:
Recordemos que lo primordial en los problemas de física, es anotar nuestros datos:
m1 = 3kg
m2 = 400 kg
v1 = 500 m/s
Si analizamos las condiciones del problema, nos daremos cuenta que el proyectil y el cañón están en total reposo antes del disparo, por lo que la cantidad de movimiento inicial es cero, entonces:
$\displaystyle 0={{m}_{1}}{{v}_{1}}+{{m}_{2}}{{v}_{2}}$
Recordemos que lo que queremos encontrar es a v2 así que despejamos:
$\displaystyle -{{m}_{1}}{{v}_{1}}={{m}_{2}}{{v}_{2}}$
$\displaystyle {{v}_{2}}=-\frac{{{{m}_{1}}{{v}_{1}}}}{{{{m}_{2}}}}$
Ahora procedemos a sustituir nuestros datos en la fórmula:
$\displaystyle {{v}_{2}}=-\frac{{\left( {3kg} \right)\left( {500\frac{m}{s}} \right)}}{{400kg}}=-3.75\frac{m}{s}$
Por lo que la velocidad del retroceso del cañón es de -3.7 m/s
El signo menos indica que el cañón se mueve en sentido contrario al movimiento del proyectil.
Solución:
Vamos a considerar nuestros datos:
$\displaystyle {{m}_{1}}=0.2kg$
$\displaystyle {{U}_{1}}=4\frac{m}{s}$
$\displaystyle {{m}_{2}}=0.1kg$
$\displaystyle {{U}_{2}}=2\frac{m}{s}$
Recordemos la fórmula:
$\displaystyle {{m}_{1}}{{U}_{1}}+{{m}_{2}}{{U}_{2}}={{m}_{1}}{{v}_{1}}+{{m}_{2}}{{v}_{2}}$
Como van en sentido contrario y después del choque tienen la misma magnitud de velocidad $\displaystyle {{v}_{1}}={{v}_{2}}=v$ , por tanto:
$\displaystyle {{m}_{1}}{{U}_{1}}+\left( {-{{m}_{2}}{{U}_{2}}} \right)=\left( {{{m}_{1}}+{{m}_{2}}} \right)v$
Despejando a $\displaystyle v$
$\displaystyle v=\frac{{{{m}_{1}}{{U}_{1}}-{{m}_{2}}{{U}_{2}}}}{{{{m}_{1}}+{{m}_{2}}}}$
Sustituyendo nuestros datos, obtenemos:
$\displaystyle v=\frac{{{{m}_{1}}{{U}_{1}}-{{m}_{2}}{{U}_{2}}}}{{{{m}_{1}}+{{m}_{2}}}}=\frac{{\left( {0.2kg} \right)\left( {4\frac{m}{s}} \right)-\left( {0.1kg} \right)\left( {2\frac{m}{s}} \right)}}{{0.2kg+0.1kg}}$
$\displaystyle v=2\frac{m}{s}$
Por lo que la velocidad es de 2 m/s
Solución:
Anotamos los datos del problema:
$\displaystyle {{m}_{1}}=0.012kg$
$\displaystyle {{m}_{2}}=9kg$
$\displaystyle {{U}_{2}}=0$
$\displaystyle {{U}_{1}}=?$
$\displaystyle v=0.4\frac{m}{s}$
Como el trozo de madera está en reposo, la única cantidad de movimiento inicial se debe a la bala y como después del impacto los dos cuerpos llevan la misma magnitud de la velocidad $\displaystyle v$ , la fórmula se reduce a:
$\displaystyle {{m}_{{\acute{\ }1}}}{{U}_{1}}=\left( {{{m}_{1}}+{{m}_{2}}} \right)v$
Dónde $\displaystyle {{U}_{1}}$
$\displaystyle {{U}_{1}}=\frac{{\left( {{{m}_{1}}+{{m}_{2}}} \right)v}}{{{{m}_{{\acute{\ }1}}}}}$
Sustituyendo nuesros datos en la fórmula:
$\displaystyle {{U}_{1}}=\frac{{\left( {0.012kg+9kg} \right)(0.4\frac{m}{s})}}{{0.012kg}}=300.4\frac{m}{s}$
Por lo que la velocidad inicial de la bala fue de 300.4 m/s
Solución:
Como es un choque elástico, se conserva tanto el momento como la energía cinética.
Dado que las masas son iguales y la bola B está inicialmente en reposo, las velocidades finales de las bolas serán intercambiadas:
$\displaystyle {{v}_{1}}=0\frac{m}{s}$ (la bola A se detiene)
$\displaystyle {{v}_{2}}=2\frac{m}{s}$ (la bola B se mueve con la velocidad inicial de la bola A)
Por lo tanto, la bola A se detiene y la bola B se mueve con una velocidad de 2 m/s.
Solución:
En un choque inelástico, se conserva el momento, pero no la energía cinética.
Anotamos los datos:
$\displaystyle {{m}_{1}}=1000kg$
$\displaystyle {{U}_{1}}=20\frac{m}{s}$
$\displaystyle {{m}_{2}}=2000kg$
$\displaystyle {{U}_{2}}=5\frac{m}{s}$
$\displaystyle {{v}_{1}}={{v}_{2}}$
Consideramos nuestra fórmula:
$\displaystyle {{m}_{1}}{{U}_{1}}+{{m}_{2}}{{U}_{2}}={{m}_{1}}{{v}_{1}}+{{m}_{2}}{{v}_{2}}$
Como las velocidades serán iguales, debemos simplificarlas de esta manera:
$ \displaystyle {{m}_{1}}{{U}_{1}}+{{m}_{2}}{{U}_{2}}=\left( {{{m}_{1}}+{{m}_{2}}} \right)v$
Sustituyendo nuestros datos:
$\displaystyle \left( {1000kg} \right)\left( {20\frac{m}{s}} \right)+\left( {2000kg} \right)\left( {5\frac{m}{s}} \right)=\left( {1000kg+2000kg} \right)v$
$\displaystyle 20000+10000=\left( {3000} \right)v$
$\displaystyle 30000=\left( {3000} \right)v$
Despejando a "v"
$\displaystyle v=\frac{{30000}}{{3000}}=10\frac{m}{s}$
Por lo que la velocidad después del choque será de 10 m/s
Deja una respuesta

Estos temas te pueden interesar