Conversión de Escalas de Temperatura

En Fisimat nos enfocamos en los ejercicios resueltos paso a paso para lograr un objetivo de aprendizaje por medio de problemas, en esta ocasión hablaremos sobre las diferentes escalas termométricas o de temperatura y aprenderemos a convertir de una escala a otra, esta conversión de unidades de temperatura son muy importantes para comprender temas de termología en física.

¿Qué escalas conocemos?

Actualmente se utilizan tres escalas, las escalas Fahrenheit, Celsius y Kelvin. Esto en honor a los científicos quienes descubrieron cada caso particular.

Gabriel Farenheit fue un alemán nacido en 1686 y fallecido en 1736, soplador de vidrio y fabricante de instrumentos que contribuyó en la construcción del primer termómetro basado en una mezcla de hielo y cloruro de amonio y registró el nivel que alcanzaba el mercurio a una temperatura muy baja, volvió a marcar el termómetro y entre ambas señales hizo 96 divisiones iguales. Más tarde, observó que, al colocar su termómetro en una mezcla de hielo en fusión y agua, registraba una lectura de 32°F y al colocarlo en agua hirviendo leía 212°F.

Andres Celsius fue un biólogo sueco que en 1742 basó su escala en el punto de fusión del hielo (0 °C) y en el punto de ebullición del agua (100 °C) a la presión de una atmósfera o sea 760 mm de Hg, es decir, dividió su escala en 100 partes iguales, cada una de 1 °C.

William Kelvin fue un científico inglés que propuso una nueva escala de temperatura, en la cual el cero corresponde a lo que tal vez sea la menor temperatura posible llamada cero absoluto , en esta temperatura la energía cinética de las moléculas es cero. El tamaño de un grado de la escala Kelvin es igual al de un grado Celsius y el valor de cero grados en la escala de Celsius equivale a 273 K, tal como se ilustra en la imagen de abajo. Cuando la temperatura se da en Kelvin se dice que es absoluta y ésta es la escala aceptada por el Sistema Internacional de Unidades (SI).

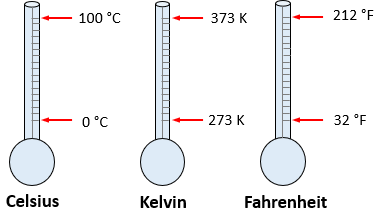
Comparación entre escalas

La pregunta que nos podemos hacer, es ¿cómo podemos llegar a la comparación de escalas y como se obtienen las fórmulas para convertir una unidad a otra?. Para ello ocuparemos el teorema de Tales, considerando las siguientes escalas Celsius y Fharenheit.

1. La temperatura de fusión del hielo corresponde, en la escala Celsius, a 0°C y, en la escala Fahrenheit, a 32°F.
2. La temperatura del agua hirviendo corresponde a 100°C en la escala Celsius y 212°F en la escala Fahrenheit.
3. La escala Fahrenheit tiene 180 divisiones (212 - 32), correspondientes a 100 divisiones (100 - 0) en la escala Celcius.

Relacionando las dos escalas, tenemos:

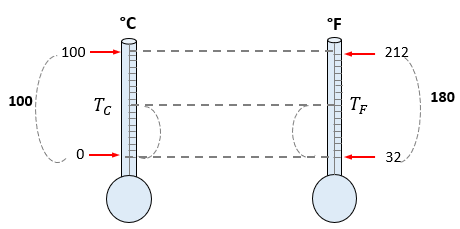
Aplicando el teorema de Tales, podemos relacionar lo siguiente:

$\displaystyle \frac{{{{T}_{F}}-32}}{{212-32}}=\frac{{{{T}_{C}}-0}}{{100-0}}$

En ambas igualdades, se resta primero la temperatura °C y °F con la de fusión de ambos, y en el denominador se resta las de ebullición con las de fusión:

$\displaystyle \frac{{{{T}_{F}}-32}}{{180}}=\frac{{{{T}_{C}}-0}}{{100}}$

Multiplicando cruzada la igualdad:

$\displaystyle 100\left( {{{T}_{F}}-32} \right)=180\left( {{{T}_{C}}-0} \right)$

$\displaystyle 100\left( {{{T}_{F}}-32} \right)=180\left( {{{T}_{C}}} \right)$

$\displaystyle {{T}_{F}}-32=\frac{{180\left( {{{T}_{C}}} \right)}}{{100}}$

$\displaystyle {{T}_{F}}-32=1.8{{T}_{C}}$

Despejando a "TF"

$\displaystyle {{T}_{F}}=1.8{{T}_{C}}+32$

Y de esta manera podemos obtener la fórmula de conversión de una unidad de temperatura a otra.

Fórmulas para transformar unidades de temperatura a otra

1️⃣ Para transformar de grados Celsius a Kelvin:

2️⃣ Para transformar de Kelvin a grados Celsius:

3️⃣ Para transformar de grados Celsius a grados Fahrenheit:

4️⃣ Para transformar de grados Fahrenheit a grados Celsius:

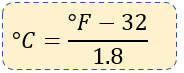
Ejercicios Resueltos de Conversión de Escalas de Temperatura

Ahora es momento de convertir unidades de temperatura, o transformación unidades de temperatura en otra.

Solución:

Lo primero que haremos será ubicar la fórmula, en este caso debemos convertir de grados Celsius a Kelvin.

$\displaystyle K={}^\circ C+273$

Ahora debemos agregar los 120°C en la fórmula:

$\displaystyle K=120+273=393$

$\displaystyle K=393K$

Por lo que la respuesta es de 393K

Solución:

Con analizar el problema podemos darnos cuenta que utilizaremos la fórmula de convertir Kelvin a Celsius.

$\displaystyle {}^\circ C=K-273$

Ahora debemos agregar los 273K en la fórmula:

$\displaystyle {}^\circ C=273K-273$

$\displaystyle {}^\circ C=0{}^\circ C$

Por lo que la respuesta es de 0 °C

Solución:

A simple vista podemos darnos cuenta que utilizaremos la fórmula 3, donde convertimos de grados Celsius a grados Fahrenheit

$\displaystyle {}^\circ F=1.8{}^\circ C+32$

Ahora debemos agregar los 25°C  en la fórmula:

$\displaystyle {}^\circ F=1.8\left( {25{}^\circ C} \right)+32$

$\displaystyle {}^\circ F=45{}^\circ C+32$

$\displaystyle {}^\circ F=77{}^\circ C$

Por lo que la respuesta es de 77°C

Solución:

Utilizaremos la cuarta fórmula para poder convertir de grados Fahrenheit a Celsius, entonces:

$\displaystyle {}^\circ C=\frac{{{}^\circ F-32}}{{1.8}}$

Ahora debemos agregar los 414°F en la fórmula:

$\displaystyle {}^\circ C=\frac{{414{}^\circ F-32}}{{1.8}}$

$\displaystyle {}^\circ C=\frac{{382}}{{1.8}}{}^\circ C$

$\displaystyle {}^\circ C=212.22{}^\circ C$

Por lo que la respuesta es de 212.22°C

Solución:

Si nos damos cuenta, solamente podemos convertir directamente de Fahrenheit a Celsius y de Celsius a Kelvin, por lo que será el método que usaremos.

$\displaystyle {}^\circ C=\frac{{-58{}^\circ F-32}}{{1.8}}$

$\displaystyle {}^\circ C=\frac{{-90}}{{1.8}}$

$\displaystyle {}^\circ C=-50{}^\circ C$

Por lo tanto los -58°F son -50°C

Ahora convertimos a Kelvin

$\displaystyle K={}^\circ C+273$

Sustituyendo los -50°C

$\displaystyle K=-50+273$

$\displaystyle K=223$

Por lo que sería 223 K

Listo!

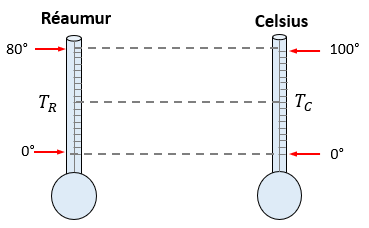
Solución:

Hacemos la comparación que se hizo al comienzo de este artículo, aplicando el teorema de Tales:

$\displaystyle \frac{{{{T}_{R}}-0}}{{80-0}}=\frac{{{{T}_{C}}-0}}{{100-0}}$

Realizando las restas correspondientes:

$\displaystyle \frac{{{{T}_{R}}}}{{80}}=\frac{{{{T}_{C}}}}{{100}}$

Simplificando, por "20" en cada denominador, manteniendo la misma proporción:

$\displaystyle \frac{{{{T}_{R}}}}{4}=\frac{{{{T}_{C}}}}{5}$

Despejando a TR

$\displaystyle {{T}_{R}}=\frac{{4{{T}_{C}}}}{5}$

Ahora sustituimos los "35°C" en la fórmula:

$\displaystyle {{T}_{R}}=\frac{{4{{T}_{C}}}}{5}=\frac{4}{5}\left( {35} \right)$

$\displaystyle {{T}_{R}}=28{}^\circ R$

Obtenemos 28°R como respuesta a este problema.