Ecuación de Continuidad - Ejercicios Resueltos

Seguimos redactando artículos y ejercicios sobre los temas de hidráulica, en el área de Física, y en esta ocasión tenemos la oportunidad de redactar sobre la ecuación de continuidad y ver la gran importancia que tiene ésta ecuación, e incluso hacemos uso de ella sin tenerlo en cuenta. Pero bueno, vamos a comenzar detallando que la ecuación de continuidad de los fluidos está expresada matemáticamente de la siguiente manera:
? Fórmula de la ecuación de continuidad
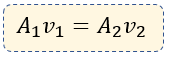
$\displaystyle {{A}_{1}}{{v}_{1}}={{A}_{2}}{{v}_{2}}$
De la fórmula podemos deducir que A es área y v es velocidad. Más adelante lo explicaremos mejor, por ahora veamos la siguiente imagen, para aclarar mejor nuestro panorama sobre éste tema.
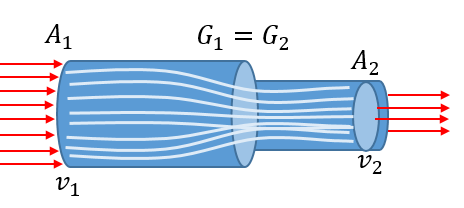
Bien, si observas la imagen te darás cuenta que en nuestra ecuación de continuidad, estamos haciendo referencia al producto del área y la rapidez del fluido. Esto suele ser constante para un fluido incompresible. Y también nos damos cuenta que la rapidez es alta donde el tubo es estrecho, y baja donde el tubo es ancho, por lo que el gasto permanece constante en ambos lados del tubo. 😀
Una aplicación muy sencilla del fenómeno de la continuidad se puede observar al momento que alguien riega un poco de agua a través de una manguera, ya que allí se puede apreciar como al momento de presionar la salida de la manguera (o sea se reduce el caudal por donde sale el agua), vemos como el chorro de agua sale más disparada, aquí es donde comprobamos dicho concepto. Bien, ahora es momento de poner en práctica la teoría.
? Ejercicios Resueltos de Continuidad
Como es costumbre, no podemos dar por completo un tema sino tenemos los ejercicios necesarios para darlo por hecho.
Solución:
Lo primero será recaudar nuestros datos implícitos en el problema.
$\displaystyle {{d}_{1}}=3.9cm\left( \frac{1m}{100cm} \right)=0.039m$
$\displaystyle {{v}_{1}}=4.5\frac{m}{s}$
$\displaystyle {{d}_{2}}=2.25cm\left( \frac{1m}{100cm} \right)=0.0225m$
$\displaystyle {{v}_{2}}=?$
Bien, si nos damos cuenta no tenemos el área, pero si tenemos los diámetros de la tubería, lo que nos facilita poder obtener las áreas. Así que procedemos a calcularlas.
$\displaystyle {{A}_{1}}=\frac{\pi {{d}_{1}}^{2}}{4}=\frac{\pi {{(0.039m)}^{2}}}{4}=1.19x{{10}^{-3}}{{m}^{2}}$
Luego con la otra:
$\displaystyle {{A}_{2}}=\frac{\pi {{d}_{2}}^{2}}{4}=\frac{\pi {{(0.0225m)}^{2}}}{4}=0.398x{{10}^{-3}}{{m}^{2}}$
Con lo que establecemos, la ecuación de continuidad y despejamos nuestra incógnita.
$\displaystyle {{A}_{1}}{{v}_{1}}={{A}_{2}}{{v}_{2}}$
Despejando:
$\displaystyle {{v}_{2}}=\frac{{{A}_{1}}{{v}_{1}}}{{{A}_{2}}}$
Sustituyendo datos:
$\displaystyle {{v}_{2}}=\frac{{{A}_{1}}{{v}_{1}}}{{{A}_{2}}}=\frac{(1.19x{{10}^{-3}}{{m}^{2}})(4.5\frac{m}{s})}{0.398x{{10}^{-3}}{{m}^{2}}}=13.5\frac{m}{s}$
Por lo que la velocidad del agua en la salida, será de 13.5 m/s
Solución:
Nuevamente recolectamos los datos del problema.
$\displaystyle {{A}_{1}}=\frac{\pi {{d}_{1}}^{2}}{4}=\frac{\pi {{(0.25m)}^{2}}}{4}=0.0491{{m}^{2}}$
$\displaystyle {{A}_{2}}=\frac{\pi {{d}_{2}}^{2}}{4}=\frac{\pi {{(0.1m)}^{2}}}{4}=7.85x{{10}^{-3}}{{m}^{2}}$
$ \displaystyle {{v}_{1}}=10.5\frac{m}{s}$
$\displaystyle {{v}_{2}}=?$
Con eso nos damos cuenta, que variable despejar y como sustituir nuestros datos:
$\displaystyle {{v}_{2}}=\frac{{{A}_{1}}{{v}_{1}}}{{{A}_{2}}}=\frac{(0.0491{{m}^{2}})(10.5\frac{m}{s})}{7.85x{{10}^{-3}}{{m}^{2}}}=65.68\frac{m}{s}$
Lo que podemos observar que es una rapidez increíble.
? Ejercicios para Practicar de Ecuación de Continuidad
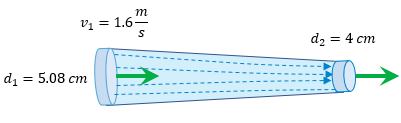
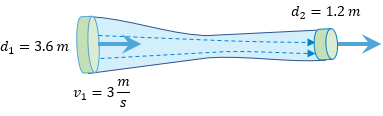
-
alguien me podria ayudar
Problema n° 1
Calcular el volumen de agua que pasa en 18 s por una cañería de 3 cm² de sección si la velocidad de la corriente es de 40 cm/s.
Problema n° 2
Una corriente estacionaria circula por una tubería que sufre un ensanchamiento. Si las secciones son de 1,4 cm² y 4,2 cm² respectivamente, ¿cuál es la velocidad de la segunda sección si en la primera es de 6 m/s?
Problema n° 3
El caudal de una corriente estacionaria es de 600 l/min. Las secciones de la tubería son de 5 cm² y 12 cm². Calcule la velocidad de cada sección.
Problema n° 4
La velocidad de una corriente estacionaria es de 50 cm/s y su caudal de 10 l/s. ¿Cuál es la sección del tubo?
Problema n° 5
Por un tubo de 15 cm² de sección sale agua a razón de 100 cm/s. Calcule la cantidad de litros que salen en 30 minutos.
Problema n° 6
Por un caño de 5 cm² de sección surgen 40 dm³/minuto. Determinar la
AYUDA PORFAVOR -
3.- Por una tubería de 6 cm de diámetro circula agua. En una parte de la tubería hay un
estrechamiento y el diámetro es de 1.5 cm, con una velocidad en este punto de 9 m/s ¿qué
velocidad llevará el agua en la tubería de diámetro mayor?AUYUDAA
-
Una tubería que tiene una velocidad de salida de 2 m/s en un área de
1.5cm 2 , si la velocidad del área mayor es de 0.5 m/s. ¿Cuál es el radio de la
tubería del área mayor en cm? -
¿Cuál será la velocidad en una tubería que tiene una sección de 10 cm de
diámetro en su parte del estrechamiento y proviene de un área de 1964 cm 2
con una velocidad de 1.2m/s? -
Hola, me puedes ayudar con un problema? solo me dan dos datos
Problema 1.- Retomando el problema sobre la ecuación de Bernoulli que se describe
en la siguiente liga
https://www.youtube.com/watch?v=EP8nhOs9T-I
a) Calcule la velocidad, la presión del agua y el caudal en un punto intermedio,
donde el área de la tubería es de 0.2 m2 y la altura es de 0.4 m.
b) Incluya la ecuación de Bernoulli y la ecuación de continuidad.
Si tiene que eliminar algún término en la aplicación de las ecuaciones, explique la
razón.
c) Agrega las unidades de todas las variables y describe paso a paso la resolución
del problema.
d) Menciona que representa cada término de las ecuaciones.Muchas gracias
33 Deja tu comentario
Deja una respuesta

Estos temas te pueden interesar