Ecuación de la Circunferencia con Centro fuera del Origen

Cuando hemos aprendido a resolver e interpretar ejercicios basados en la Ecuación de la Circunferencia con centro el origen, nos topamos con un caso más peculiar que se trata de la ecuación de la circunferencia con centro fuera del origen. Y esto hace que nuestro cálculo sean un poco más diferentes a los anteriores. Pero nada complicado 😀

Si bien, en la ecuación de la circunferencia con centro en el origen usamos la forma canónica, en el caso de la ecuación fuera del origen, utilizaremos la forma ordinaria. Qué podemos apreciar en la siguiente fórmula:

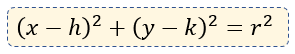
Ecuación de la Circunferencia fuera del origen

Qué de forma gráfica está representada, como se muestra en la imagen:

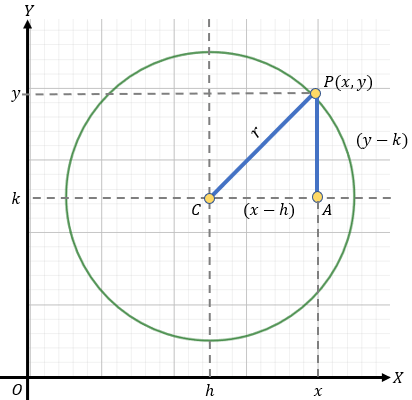
Circunferencia Fuera del Origen

Ejercicios Resueltos de la Ecuación de la Circunferencia fuera del origen

Veamos como resolver problemas de la circunferencia cuando su centro está fuera del origen, estos ejemplos harán que nuestro conocimiento sea más profundo conforme se avanzan en los temas de geometría analítica y el estudio de cónicas.

Ejemplo 1. Determinar la ecuación de la circunferencia cuyo centro es el punto C (5, -3) y su radio es de √19

Solución:

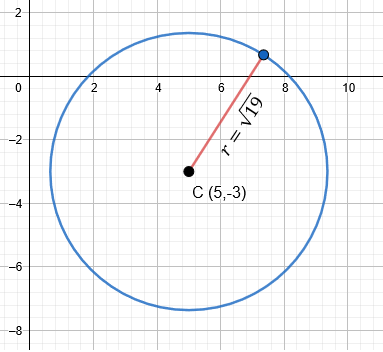
Vamos a sustituir nuestros datos en la ecuación ordinaria de la circunferencia, porque es lo que el problema nos pide. Nuestros datos serán los siguientes:

h = 5

k = -3

r = √19

Y la ecuación ordinaria es:

$\displaystyle {{(x-h)}^{2}}+{{(y-k)}^{2}}={{r}^{2}}$

Al sustituir tendremos lo siguiente:

$\displaystyle {{(x-5)}^{2}}+{{(y-(-3))}^{2}}={{\left( \sqrt{19} \right)}^{2}}$

Realizando las operaciones indicadas, tenemos:

Resultado:

$\displaystyle {{(x-5)}^{2}}+{{(y+3)}^{2}}=19$

La respuesta es hasta este punto, porque nos piden solamente la ecuación en su forma ordinaria. No nos piden la ecuación en su forma general, como se verá en el siguiente ejemplo. Pero antes, debemos mostrar como se ve la gráfica de este ejemplo 1.

Circunferencia fuera del origen

Ejemplo 2. Encuentra la ecuación general de la circunferencia con centro en (2, - 1) y radio 6

Solución:

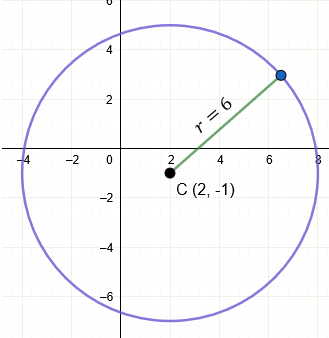
A diferencia del ejemplo anterior, en este problema nos piden la ecuación general de la circunferencia, por lo que el proceso final será "un poco diferente", veamos primero nuestros datos:

h = 2

k = -1

r = 6

Nuestra fórmula o ecuación ordinaria es:

$\displaystyle {{(x-h)}^{2}}+{{(y-k)}^{2}}={{r}^{2}}$

Sustituyendo nuestros datos en la fórmula, tenemos que:

$\displaystyle {{(x-2)}^{2}}+{{(y-(-1))}^{2}}={{\left( 6 \right)}^{2}}$

Realizando las operaciones indicadas

$\displaystyle {{(x-2)}^{2}}+{{(y+1)}^{2}}=36$

Hasta este punto tenemos la forma ordinaria, sin embargo, para poder dar con la ecuación general tenemos que resolver los binomios, reducir e igualar a cero.

$\displaystyle {{x}^{2}}-4x+4+{{y}^{2}}+2y+1=36$

Simplificando e igualando a cero

$\displaystyle {{x}^{2}}+{{y}^{2}}-4x+2y+5=36$

$\displaystyle {{x}^{2}}+{{y}^{2}}-4x+2y+5-36=0$

Reduciendo, finalmente tenemos:

Resultado:

$\displaystyle {{x}^{2}}+{{y}^{2}}-4x+2y-31=0$

Ecuación de la Circunferencia fuera del Origen

Veamos otro ejemplo, pero sin tener al radio como dato, es decir que lo vamos a encontrar.

Ejemplo 3. Determine la ecuación general de la circunferencia, si el centro está en las coordenadas (7, -4) y dicha circunferencia pasa por el punto (-5, 1).

Solución:

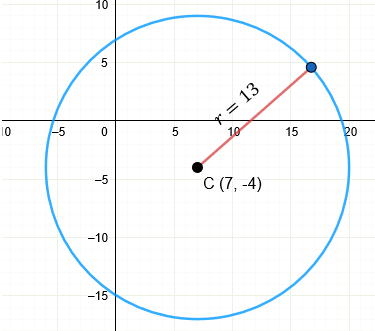
En este ejemplo, no nos dan el radio. Pero si nos indican que la circunferencia tiene centro en (7 , -4) y que en uno de los puntos donde pasa la circunferencia es el punto (-5, 1). Este es un dato importante, porque nos están indicando la dimensión del radio. Solo debemos saber que distancia hay desde el centro hasta el punto de la circunferencia.

Entonces aplicamos la fórmula de la distancia entre dos puntos.

$\displaystyle d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$

En vez de colocar "d" pondremos "r", ya que estamos haciendo referencia al radio.

$\displaystyle r=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$

Sustituimos nuestros datos en la fórmula:

$\displaystyle r=\sqrt{{{\left( 7-(-5) \right)}^{2}}+{{\left( (-4-1 \right)}^{2}}}$

Resolviendo.

$\displaystyle r=\sqrt{{{(12)}^{2}}+{{(-5)}^{2}}}=\sqrt{144+25}=\sqrt{169}=13$

Entonces podemos decir que nuestro centro es C (7, -4) y nuestro radio = 13. Sustituyendo estos datos en la ecuación ordinaria, tenemos:

$\displaystyle {{(x-h)}^{2}}+{{(y-k)}^{2}}={{r}^{2}}$

Recordar que:

h = 7

k = -4

r = 13

$\displaystyle {{(x-7)}^{2}}+{{(y-(-4))}^{2}}={{\left( 13 \right)}^{2}}$

Reduciendo.

$\displaystyle {{(x-7)}^{2}}+{{(y+4)}^{2}}=169$

Resolviendo el binomio, obtenemos

$\displaystyle {{x}^{2}}-14x+49+{{y}^{2}}+8y+16-169=0$

Dónde, finalmente tenemos la ecuación general de la circunferencia.

Resultado:

$\displaystyle {{x}^{2}}+{{y}^{2}}-14x+8y-104=0$

Ecuación de la Circunferencia Fuera del Origen

Carlos julián

Carlos Julián es Ingeniero Mecatrónico, profesor de Física y Matemáticas.

Temas que podrían interesarte 👇

3 Comentarios Publicados

Brigitte Moreno dice:

19 noviembre, 2021 a las 8:44 am

ayúdeme:
Su centro es el origen y tiene radio 6

Responder
Brigitte Moreno dice:

19 noviembre, 2021 a las 8:45 am

ayúdeme:
Su centro es el origen y tiene radio 15/2

Responder
eduardo dice:

30 noviembre, 2021 a las 9:17 pm

x^2+y^2=36

Responder

Deja una respuesta Cancelar la respuesta