Ecuación de la Elipse con Centro fuera del Origen

Antes de comenzar este artículo es importante que el alumno/a esté familiarizado con el tema de la elipse con centro en el origen, puesto que desde ese tema se tocarán los mismos elementos de la elipse y solamente comprenderemos las nuevas ecuaciones para una elipse con centro fuera del origen.

? Ecuación y Elementos de la Elipse 

Tres de los elementos más importantes de la elipse tendrán una fórmula diferente a las de una elipse con centro en el origen, principalmente el vértice, los focos y los extremos del eje menor. Veamos 😀

? Elipse Horizontal con centro en (h,k)

La ecuación particular de dicha elipse es la siguiente:

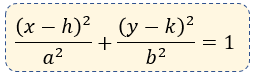
Si el eje focal es horizontal.

Elementos

1️⃣ Vértice:

$latex \displaystyle V(h\pm a,k)$

2️⃣ Focos:

$latex \displaystyle F(h\pm c,k)$

3️⃣ Extremos del eje menor "B":

$latex \displaystyle B(h,k\pm b)$

? Elipse Vertical con centro en (h,k)

La ecuación particular de dicha elipse es la siguiente:

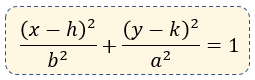
Si el eje focal es vertical en donde debe cumplirse que a > b

Elementos

1️⃣ Vértice:

$latex \displaystyle V(h,k\pm a)$

2️⃣ Focos:

$latex \displaystyle F(h,k\pm c)$

3️⃣ Extremos del eje menor "B":

$latex \displaystyle B(h\pm b,k)$

Ecuación general de la Elipse:

La ecuación general de la elipse es la siguiente:

$latex \displaystyle A{{x}^{2}}+C{{y}^{2}}+Dx+Ey+F=0$

Con A ≠ C , y ambas cantidades de igual signo.

? Ejercicios Resueltos de la Ecuación de la Elipse con Centro fuera del Origen

Comencemos a resolver algunos ejemplos de la ecuación de la elipse. Veamos:

Solución:

En este primer paso, vamos agrupar en el lado izquierdo de la igualdad a los términos que contengan las mismas variables y del miembro derecho se colocan las constantes. De esta forma:

$latex \displaystyle \left( 4{{x}^{2}}-16x \right)+\left( 9{{y}^{2}}+18y \right)=11$

Ahora vamos a factorizar en cada grupo el coeficiente del término cuadrado:

$latex \displaystyle 4\left( {{x}^{2}}-4x \right)+9\left( {{y}^{2}}+2y \right)=11$

Se completa el trinomio al cuadrado perfecta en cada grupo, recordar que se agrega el mismo valor en el miembro derecho.

$latex \displaystyle 4\left( {{x}^{2}}-4x+{{\left( \frac{4}{2} \right)}^{2}} \right)+9\left( {{y}^{2}}+2y+{{\left( \frac{2}{2} \right)}^{2}} \right)=11+16+9$

De aquí obtenemos:

$latex \displaystyle 4\left( {{x}^{2}}-4x+4 \right)+9\left( {{y}^{2}}+2y+1 \right)=36$

Factorizando lo de los paréntesis, obtenemos:

$latex \displaystyle 4{{\left( x-2 \right)}^{2}}+9{{\left( y+1 \right)}^{2}}=36$

Se dividen ambos lados de la igualdad por 36 y se simplifica.

$latex \displaystyle \frac{4{{\left( x-2 \right)}^{2}}}{36}+\frac{9{{\left( y+1 \right)}^{2}}}{36}=\frac{36}{36}$

Obtenemos lo siguiente:

$latex \displaystyle \frac{{{\left( x-2 \right)}^{2}}}{9}+\frac{{{\left( y+1 \right)}^{2}}}{4}=1$

Dónde:

$latex \displaystyle {{a}^{2}}=9$

$latex \displaystyle {{b}^{2}}=4$

Al ser el denominador mayor "9" que está justo debajo de "x", entonces decimos que se trata de una elipse horizontal. 

También podemos apreciar que:

a = 3

b = 2

Y para obtener c , se puede obtener de la siguiente manera:

$latex \displaystyle c=\sqrt{{{a}^{2}}-{{b}^{2}}}=\sqrt{9-4}=\sqrt{5}=2.23$

c ≈ 2.23

De aquí podemos deducir los elementos de dicha elipse:

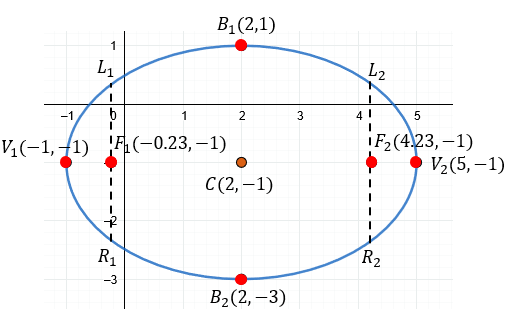
1️⃣ Obteniendo el Centro:

De la ecuación (x - h) tenemos (x - 2), por lo que

h = 2

De la ecuación (y - k) tenemos (y+1), por lo que

k = -1

Finalmente, el centro posee coordenadas:

C(2, -1)

2️⃣ Obteniendo el lado recto

$latex \displaystyle \overline{LR}=\frac{2{{b}^{2}}}{a}$

Sustituyendo los valores:

$latex \displaystyle \overline{LR}=\frac{2{{b}^{2}}}{a}=\frac{2{{(2)}^{2}}}{3}=\frac{8}{3}\approx 2.66$

3️⃣ Obteniendo la excentricidad

$latex \displaystyle e=\frac{c}{a}=\frac{2.23}{3}=0.743$

4️⃣ Obteniendo el Vértice

El vértice para una elipse horizontal, tiene la fórmula:

$latex \displaystyle V(h\pm a,k)$

Entonces, las dos coordenadas para los vértices son:

$latex \displaystyle {{V}_{2}}(2+3,-1)=(5,-1)$

$latex \displaystyle {{V}_{1}}(2-3,-1)=(-1,-1)$

5️⃣ Obteniendo los Focos

Los focos para una elipse horizontal, tiene la fórmula:

$latex \displaystyle F(h\pm c,k)$

Entonces, las dos coordenadas para los focos son:

$latex \displaystyle {{F}_{1}}(2-2.23,-1)={{F}_{1}}(-0.23,-1)$

$latex \displaystyle {{F}_{2}}(2+2.23,-1)={{F}_{2}}(4.23,-1)$

6️⃣ Obteniendo los extremos del eje menor

Los extremos del eje menor, tiene la fórmula:

$latex \displaystyle B(h,k\pm b)$

Entonces, las dos coordenadas para los extremos del eje menor son:

$latex \displaystyle {{B}_{1}}(2,-1+2)={{B}_{1}}(2,1)$

$latex \displaystyle {{B}_{2}}(2,-1-2)={{B}_{2}}(2,-3)$

7️⃣ Gráfica de la Elipse