Ecuación de la Hipérbola con Centro en el Origen
La Hipérbola es la última forma geométrica que se estudia en la geometría analítica. Después de analizar las demás cónicas, lo que finalmente se tiene que comprender es el tema de las hipérbolas. En este artículo hablaremos a fondo sobre la Ecuación de la Hipérbola con Centro en el Origen.
En algunos textos de varios autores, la hipérbola se define de la siguiente manera:
Elementos y Ecuación de la Hipérbola
La hipérbola cuenta con varios elementos de gran importancia, que nos ayudarán a encontrar ya sea la ecuación general o incluso a partir de la ecuación general obtener sus elementos. Entre los elementos encontramos a los vértices, los focos, lado recto, las asíntotas, los extremos del eje conjugado y el centro.
Tanto para las hipérbolas horizontales, como verticales. Se debe cumplir lo siguiente:
1️⃣ Condición:
$\displaystyle {{c}^{2}}={{a}^{2}}+{{b}^{2}}$
Teniendo en cuenta que:
$\displaystyle c>b$
$\displaystyle c>a$
2️⃣ Excentricidad:
$\displaystyle e=\frac{c}{a}\left( e>1 \right)$
3️⃣ Lado Recto:
$\displaystyle \overline{LR}=\frac{2{{b}^{2}}}{a}$
Eje transverso: 2a
Eje conjugado: 2b
Eje focal: 2c
? Hipérbola Horizontal
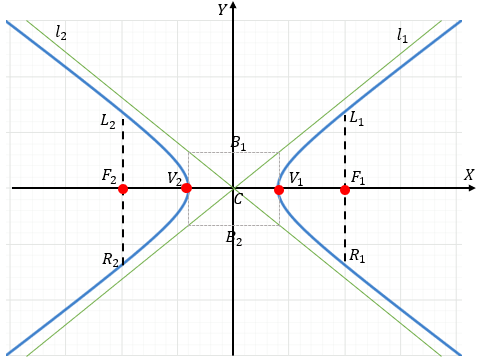
Su eje focal coincide con el eje "x"
Ecuación Canónica
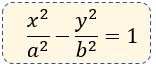
Elementos de la Hipérbola
Los elementos más importantes en la hipérbola son los vértices, focos, extremos del eje conjugado y las ecuaciones de las asíntotas.
1️⃣ Vértices:
$\displaystyle V(\pm a,0)$
2️⃣ Focos:
$\displaystyle V(\pm c,0)$
3️⃣ Extremos del eje conjugado:
$\displaystyle B(0,\pm b)$
4️⃣ Ecuaciones de las asíntotas:
$\displaystyle {{l}_{1}}:y=\frac{b}{a}x$
$\displaystyle {{l}_{2}}:y=-\frac{b}{a}x$
? Hipérbola Vertical
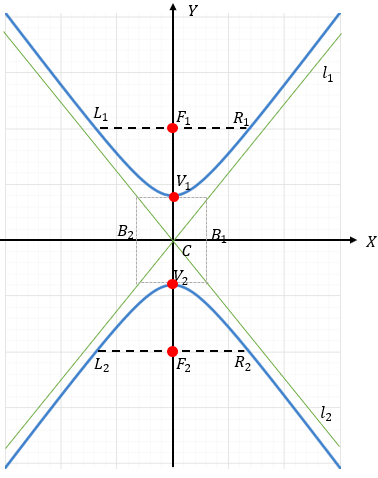
Su eje focal coincide con el eje "y"
Ecuación Canónica
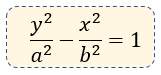
Elementos de la Hipérbola
En la hipérbola vertical, se mantienen los mismos elementos que en la hipérbola horizontal. Solo cambian sus fórmulas.
1️⃣ Vértices:
$\displaystyle V(0,\pm a)$
2️⃣ Focos:
$\displaystyle F(0,\pm c)$
3️⃣ Extremos del eje conjugado:
$\displaystyle B(\pm b,0)$
4️⃣ Ecuaciones de las asíntotas:
$\displaystyle {{l}_{1}}:y=\frac{a}{b}x$
$\displaystyle {{l}_{2}}:y=-\frac{a}{b}x$
? Ejercicios Resueltos de la Hipérbola con Centro en el Origen
Veamos algunos ejemplos resueltos de la hipérbola con centro en el origen.
Solución:
Debemos pasar la ecuación a su forma canónica, para ello lo primero que haremos será mover a -36 al segundo miembro:
$\displaystyle 9{{x}^{2}}-4{{y}^{2}}=36$
Vamos a dividir toda la ecuación sobre 36.
$\displaystyle \frac{9{{x}^{2}}}{36}-\frac{4{{y}^{2}}}{36}=\frac{36}{36}$
Simplificando, esto nos da:
$\displaystyle \frac{{{x}^{2}}}{4}-\frac{{{y}^{2}}}{9}=1$
Hemos obtenido la ecuación en su forma canónica. Observamos que la ecuación inicia con término positivo en la "x", lo que se trata de una hipérbola vertical, dónde:
$\displaystyle {{a}^{2}}=4$
$\displaystyle {{b}^{2}}=9$
Es decir:
a = 2
b = 3
Aplicando la condición, para obtener el valor de c
$\displaystyle c=\sqrt{{{a}^{2}}+{{b}^{2}}}=\sqrt{4+9}=\sqrt{13}$
c = √3
De aquí podemos deducir los elementos de dicha hipérbola:
1️⃣ Obteniendo el Vértice:
$\displaystyle V(\pm a,0)$
Es decir:
$\displaystyle {{V}_{1}}(2,0)$
$\displaystyle {{V}_{2}}(-2,0)$
2️⃣ Obteniendo los Focos:
$\displaystyle F(\pm c,0)$
Es decir:
$\displaystyle {{F}_{1}}(\sqrt{3},0)$
$\displaystyle {{F}_{2}}(-\sqrt{3},0)$
3️⃣ Extremos del eje conjugado:
$\displaystyle B(0,\pm b)$
Es decir:
$\displaystyle {{B}_{1}}(0,3)$
$\displaystyle {{B}_{2}}(0,-3)$
4️⃣ Asíntotas:
Calculando la primer asíntota
$\displaystyle {{l}_{1}}:y=\frac{b}{a}x$
Sustituyendo:
$\displaystyle {{l}_{1}}:y=\frac{3}{2}x$
Igualando a cero la ecuación, tenemos:
$\displaystyle 3x-2y=0$
Calculando la segunda asíntota
$\displaystyle {{l}_{2}}:y=-\frac{3}{2}x$
Igualando a cero la ecuación, tenemos:
$\displaystyle 3x+2y=0$
5️⃣ Lado Recto:
$\displaystyle \overline{LR}=\frac{2{{b}^{2}}}{a}=\frac{2{{(3)}^{2}}}{2}=9$
6️⃣ Excentricidad:
$\displaystyle e=\frac{c}{a}=\frac{\sqrt{3}}{2}$
7️⃣ Gráfica de la Hipérbola:
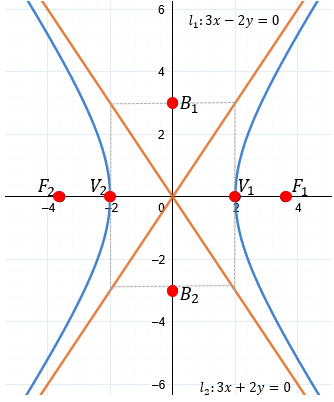
-
me ayudo mucho, pero no se si se equivoco en el ejercicio por que no seria hipérbola horizontal, por que cuando ya la grafico lo pone en horizontal y decía que era en vertical y en la ecuación es x-y= 1 lo cual es la ecuación canónica de la hipérbola horizontal esa es mi duda o no se si me pueda explicar en eso muchas gracias aun así me ayudo
-
Me ayudó muchísimo, pero tiene algunos errores y me gustaría si pudiera usted corregirlos para que los demás estudiantes como yo no se confundan. Gracias por su trabajo.
-
Se que sonará estúpido, pero, ¿Cómo identifico si una hipérbola es vertical u horizontal?
-
primero si se trata de una ecuación general tienes que convertirla a canónica, una vez hecho esto tienes que ver cual es el valor de a, el cual es el valor del denominador de la fracción positiva, la fracción de negativa es b, luego que ya observaste cual es la fracción positiva mira si en el denominador esta la X, entonces es una hipérbola horizontal, pero si esta la Y es vertical.
-
6 Deja tu comentario
Deja una respuesta

Estos temas te pueden interesar