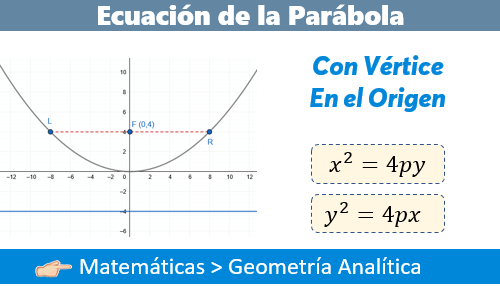
Ecuación de la Parábola con Vértice en el Origen
Dentro del fascinante mundo de la geometría analítica, la Parábola con vértice en el origen es, sin duda, uno de los temas pilares. No solo porque sirve como base para entender curvas más complejas, sino porque sus aplicaciones en física e ingeniería (como en el diseño de antenas satelitales o puentes colgantes) son infinitas.
Si has llegado aquí buscando cómo resolver ejercicios, entender las fórmulas o simplemente aprobar tu examen, estás en el lugar correcto. En este artículo, no solo te daremos las ecuaciones; te enseñaremos a "leerlas" para que nunca más confundas hacia dónde abre una gráfica.
Conceptos Fundamentales: ¿Qué es realmente una Parábola?
Antes de lanzarnos a los números, es vital entender la definición geométrica. Muchos estudiantes memorizan fórmulas, pero los verdaderos ingenieros entienden el concepto.
Definición Geométrica de la Parábola
La Parábola es el lugar geométrico de todos los puntos en el plano que se mueven de tal manera que su distancia a un punto fijo llamado foco es siempre igual a su distancia a una recta fija llamada directriz.
Esta propiedad de equidistancia es la clave mágica. No importa en qué punto de la curva te pares, la distancia hacia el "ojo" de la parábola (foco) y hacia la pared trasera (directriz) será idéntica.
Apolonio de Perge
262 a.C. - 190 a.C.
Conocido como "El Gran Geómetra", fue quien dio nombre a la parábola, elipse e hipérbola. Su trabajo sobre las secciones cónicas fue tan avanzado que pasaron siglos antes de que Kepler y Newton encontraran sus aplicaciones prácticas en la órbita de los planetas.
Elementos y Ecuación de la Parábola con Vértice en el Origen
Cuando decimos que el vértice está en el origen, nos referimos a que el punto más "curvo" de la parábola (su base o cima) se asienta perfectamente en las coordenadas \( V(0,0) \) del plano cartesiano. Esto simplifica enormemente las ecuaciones.
Para dominar este tema, dividiremos el estudio en dos casos: cuando la parábola se acuesta (Horizontal) y cuando se mantiene de pie (Vertical).
1. La Parábola Horizontal
Imagina una "U" que ha girado 90 grados. En este caso, el eje de simetría de la parábola coincide con el eje X.
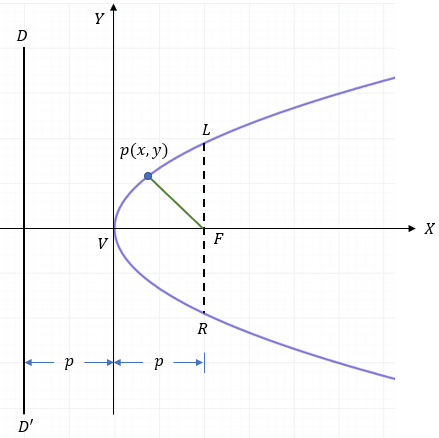
Observa la imagen superior. La letra \( p \) es el protagonista aquí. Se le llama parámetro y representa la distancia dirigida desde el vértice hasta el foco.
💡 El secreto del Parámetro P
El valor de \( p \) es como el ADN de la parábola. Si \( p \) es grande, la parábola será muy abierta (gorda). Si \( p \) es pequeño, la parábola será cerrada (flaca). Además, la distancia del vértice a la directriz también es \( p \), pero en sentido contrario.
Ecuación Canónica (Horizontal)
La fórmula que gobierna a las parábolas horizontales es:
![]()
Matemáticamente la expresamos como:
\[ y^2 = 4px \]
Elementos clave para el cálculo
Considerando que el vértice está en \( V(0,0) \), las coordenadas y ecuaciones de sus elementos son:
- Foco (F): Se encuentra sobre el eje X.
\[ F(p, 0) \] - Directriz (d): Es una recta vertical detrás del vértice.
\[ x = -p \] - Eje de Simetría: Es la recta que parte a la parábola en dos.
\[ y = 0 \quad (\text{Eje X}) \] - Lado Recto (LR): Es la cuerda que pasa por el foco y determina qué tan ancha es la parábola.
\[ LR = |4p| \]
Análisis de Concavidad (¿A dónde abre?)
El signo del parámetro \( p \) funciona como una brújula:
- Si \( p > 0 \) (positivo): La parábola abre hacia la DERECHA.
- Si \( p < 0 \) (negativo): La parábola abre hacia la IZQUIERDA.
2. La Parábola Vertical
Este es el caso clásico de la "U". Aquí, el foco descansa sobre el eje Y, y la parábola mira hacia el cielo o hacia el suelo.
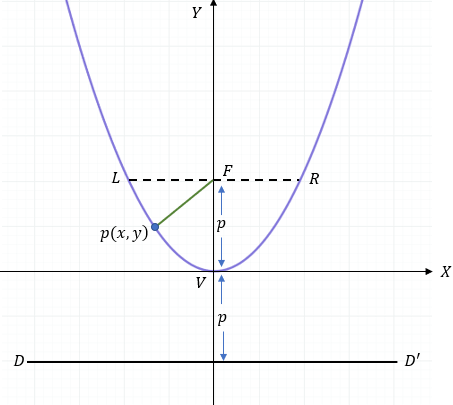
Ecuación Canónica (Vertical)
Observa cómo cambian las variables respecto a la horizontal. Ahora la \( x \) es la que está al cuadrado:
![]()
En notación matemática:
\[ x^2 = 4py \]
Elementos clave para el cálculo
Con el vértice fijo en \( V(0,0) \), tenemos:
- Foco (F): Se mueve sobre el eje Y.
\[ F(0, p) \] - Directriz (d): Ahora es una recta horizontal.
\[ y = -p \] - Eje de Simetría:
\[ x = 0 \quad (\text{Eje Y}) \] - Lado Recto (LR): La fórmula se mantiene igual.
\[ LR = |4p| \]
Análisis de Concavidad
- Si \( p > 0 \): La parábola abre hacia ARRIBA (Carita feliz 🙂).
- Si \( p < 0 \): La parábola abre hacia ABAJO (Carita triste ☹️).
Tabla Resumen: Fórmulas de la Parábola (Vértice en Origen)
Guarda esta tabla, será tu mejor amiga en los exámenes:
| Tipo | Ecuación | Foco | Directriz |
|---|---|---|---|
| Horizontal | \( y^2 = 4px \) | \( (p, 0) \) | \( x = -p \) |
| Vertical | \( x^2 = 4py \) | \( (0, p) \) | \( y = -p \) |
Ejercicios Resueltos: Dominando la Parábola paso a paso
La teoría es importante, pero la práctica hace al maestro. Vamos a resolver tres tipos de problemas clásicos que suelen aparecer en exámenes de admisión y cursos universitarios.
Ejemplo 1: Obtener elementos desde la ecuación
Encuentra las coordenadas del foco, la ecuación de la directriz y la longitud del lado recto de la parábola cuya ecuación es: \( y^2 - 4x = 0 \). Realiza su gráfica.
Solución:
Paso 1: Identificar el tipo de parábola.
Primero, debemos reescribir la ecuación dada para que se parezca a una de nuestras fórmulas canónicas. Despejamos el término cuadrático:
\[ y^2 = 4x \]
Al tener la \( y \) elevada al cuadrado, sabemos inmediatamente que es una Parábola Horizontal.
Paso 2: Encontrar el valor de \( p \).
Comparamos nuestra ecuación con la fórmula general \( y^2 = 4px \).
\[ 4px = 4x \]
Dividimos ambos lados entre \( x \) (o simplemente igualamos los coeficientes):
\[ 4p = 4 \]
\[ p = \frac{4}{4} = 1 \]
Como \( p = 1 \) (positivo), confirmamos que abre hacia la derecha.
Paso 3: Calcular los elementos.
Sustituimos \( p=1 \) en las fórmulas de la parábola horizontal:
- Foco \( F(p, 0) \):
\[ F(1, 0) \] - Directriz \( x = -p \):
\[ x = -1 \] - Lado Recto \( LR = |4p| \):
\[ LR = |4(1)| = 4 \]
Esto significa que la parábola tiene un ancho total de 4 unidades a la altura del foco (2 hacia arriba y 2 hacia abajo).
Gráfica:
Ubicamos el vértice en (0,0), el foco en (1,0) y trazamos la curva.
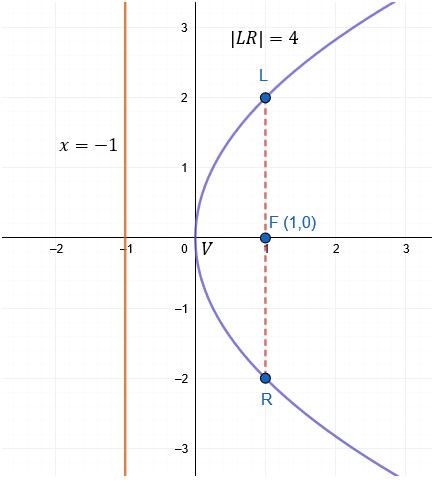
Ejemplo 2: Hallar la ecuación dado un punto
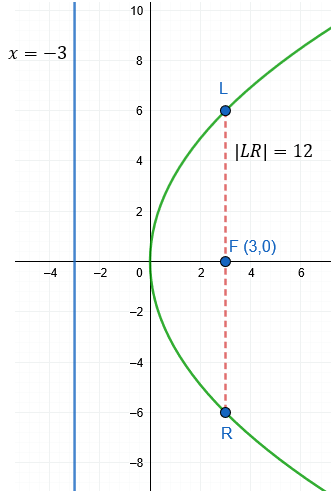
Una parábola con vértice en el origen y cuyo eje coincide con el eje X pasa por el punto \( A(3, 6) \). Determinar la ecuación de la parábola y todos sus elementos.
Solución:
Este es un problema inverso muy común. Nos dan el resultado (un punto) y nos piden la fórmula.
Paso 1: Seleccionar la ecuación correcta.
El problema nos dice "su eje coincide con el eje X". Esto es sinónimo de decir que es una Parábola Horizontal. Por tanto, usaremos:
\[ y^2 = 4px \]
Paso 2: Sustituir el punto conocido.
Sabemos que la parábola pasa por \( A(3, 6) \). Esto significa que cuando \( x=3 \), \( y=6 \). Sustituimos estos valores en la ecuación para "desbloquear" el valor de \( p \):
\[ (6)^2 = 4p(3) \]
\[ 36 = 12p \]
Despejamos \( p \):
\[ p = \frac{36}{12} = 3 \]
Paso 3: Reconstruir la ecuación y elementos.
Ahora que sabemos que \( p=3 \), la ecuación final es:
\[ y^2 = 4(3)x \quad \Rightarrow \quad \boldsymbol{y^2 = 12x} \]
Los elementos restantes son:
- Foco \( F(p,0) \): \( F(3, 0) \)
- Directriz \( x = -p \): \( x = -3 \)
- Lado Recto \( |4p| \): \( 12 \) unidades.
Gráficamente se ve así:
Ejemplo 3: Análisis de una Parábola Vertical
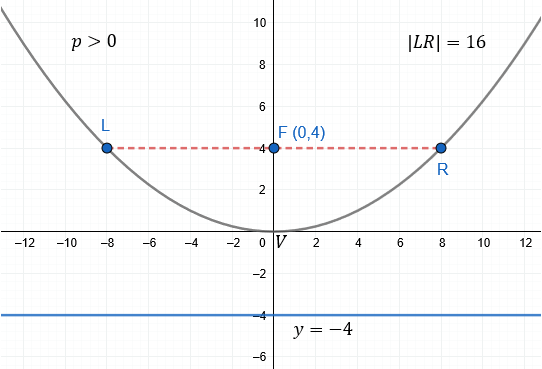
Determine los elementos de la parábola definida por la ecuación \( x^2 = 16y \).
Solución:
Paso 1: Análisis visual.
La ecuación empieza con \( x^2 \). Esto grita "¡Soy vertical!". Además, el coeficiente de \( y \) es positivo (16), así que abrirá hacia arriba.
Paso 2: Extracción del parámetro \( p \).
Igualamos con la forma canónica \( x^2 = 4py \):
\[ 4p = 16 \]
\[ p = \frac{16}{4} = 4 \]
Paso 3: Elementos.
Al ser vertical, ten cuidado de colocar las coordenadas en el orden correcto (el foco se mueve en Y, no en X):
- Ecuación: \( x^2 = 16y \)
- Foco \( F(0, p) \): \( F(0, 4) \)
- Directriz \( y = -p \): \( y = -4 \)
- Lado Recto: \( 16 \)
Ejemplo 4: Encontrar la ecuación a partir de la longitud del Lado Recto
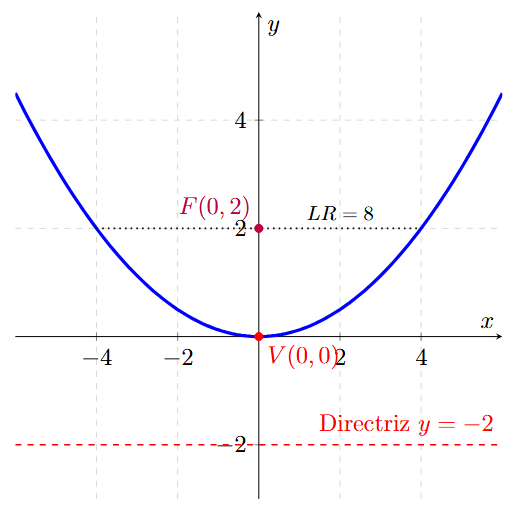
Determina la ecuación canónica de la parábola con vértice en el origen, sabiendo que es vertical y que la longitud de su lado recto es 8.
Solución:
Paso 1: Identificar el tipo de parábola y la fórmula a usar.
Se nos indica que la parábola es vertical, por lo tanto, su ecuación es de la forma \( x^2 = 4py \).
Paso 2: Utilizar la longitud del Lado Recto para encontrar \( p \).
Sabemos que la fórmula del Lado Recto es \( LR = |4p| \). El problema nos da \( LR = 8 \).
\[ |4p| = 8 \]
Esto genera dos posibles valores para \( 4p \): \( 4p = 8 \) o \( 4p = -8 \).
Caso 4A: Parábola que abre hacia ARRIBA (\( p > 0 \))
\[ 4p = 8 \quad \Rightarrow \quad p = 2 \]
Sustituyendo \( 4p=8 \) en la ecuación vertical:
\[ \boldsymbol{x^2 = 8y} \]
En este caso, el Foco es \( F(0, 2) \) y la Directriz es \( y = -2 \).
Caso 4B: Parábola que abre hacia ABAJO (\( p < 0 \))
\[ 4p = -8 \quad \Rightarrow \quad p = -2 \]
Sustituyendo \( 4p=-8 \) en la ecuación vertical:
\[ \boldsymbol{x^2 = -8y} \]
En este caso, el Foco es \( F(0, -2) \) y la Directriz es \( y = 2 \).
Ambas respuestas son matemáticamente correctas a menos que el problema especifique la concavidad (ej. "abre hacia arriba").
Ejemplo 5: Ecuación y elementos de una parábola con parámetro negativo
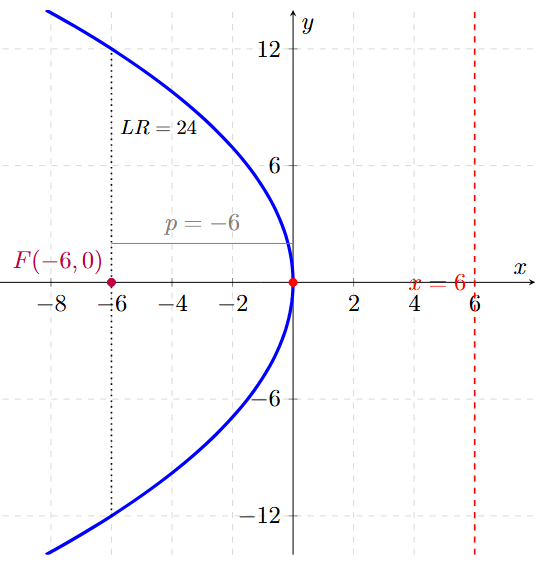
Dada la ecuación de la parábola \( y^2 + 24x = 0 \), determina todos sus elementos (Vértice, Foco, Directriz, Lado Recto) e indica su concavidad.
Solución:
Paso 1: Escribir la ecuación en la forma canónica.
Despejamos el término cuadrático \( y^2 \):
\[ y^2 = -24x \]
Al tener la \( y \) al cuadrado, es una Parábola Horizontal. El signo negativo del término de la \( x \) (\(-24x\)) nos indica que el valor de \( 4p \) es negativo, por lo tanto, la parábola abre hacia la IZQUIERDA.
Paso 2: Encontrar el valor del parámetro \( p \).
Comparamos \( y^2 = 4px \) con \( y^2 = -24x \):
\[ 4p = -24 \]
\[ p = \frac{-24}{4} \]
\[ p = -6 \]
Paso 3: Calcular los elementos.
Sustituimos \( p=-6 \) en las fórmulas de la parábola horizontal:
- Foco \( F(p, 0) \):
\[ F(-6, 0) \] - Directriz \( x = -p \):
\[ x = -(-6) \quad \Rightarrow \quad x = 6 \] - Lado Recto \( LR = |4p| \): (La longitud siempre es positiva)
\[ LR = |4(-6)| = |-24| = 24 \]
Ejemplo 6: Obtener la directriz a partir del foco
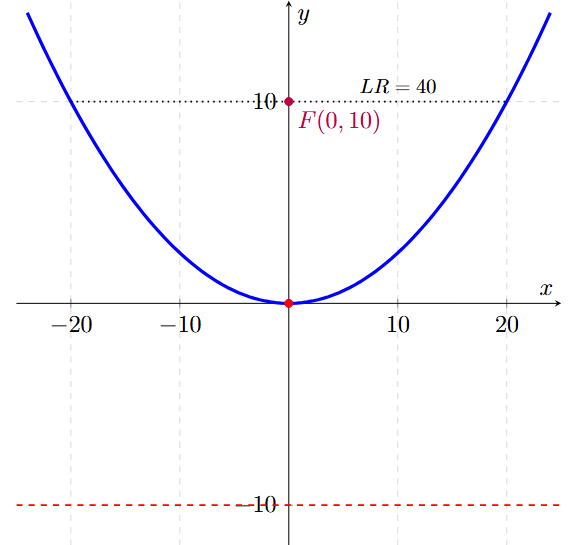
Una parábola tiene su vértice en el origen y su foco está ubicado en el punto \( F(0, 10) \). ¿Cuál es la ecuación de la directriz y la ecuación canónica de la parábola?
Solución:
Paso 1: Identificar el tipo de parábola y el parámetro \( p \).
El foco \( F(0, 10) \) tiene un valor en la coordenada \( y \), lo que indica que es una Parábola Vertical y que el valor del parámetro es \( p = 10 \).
Como \( p=10 \) (positivo), la parábola abre hacia ARRIBA.
Paso 2: Determinar la ecuación de la Directriz.
La directriz es la recta perpendicular al eje que se encuentra a la misma distancia \( p \) del vértice, pero en dirección opuesta. Para una parábola vertical, la directriz es \( y = -p \):
\[ y = -(10) \quad \Rightarrow \quad \boldsymbol{y = -10} \]
Paso 3: Determinar la Ecuación Canónica.
Usamos la fórmula vertical \( x^2 = 4py \):
\[ x^2 = 4(10)y \]
\[ \boldsymbol{x^2 = 40y} \]
⚠️ Error Común de Estudiantes
Es muy frecuente confundir las coordenadas del foco.
Recuerda:
• Si es Horizontal (\(y^2\)), el número va en la primera posición: \( (p, 0) \).
• Si es Vertical (\(x^2\)), el número va en la segunda posición: \( (0, p) \).
Reto Fisimat: ¡Ponte a prueba!
¿Crees que ya lo dominas? Intenta resolver estos problemas propuestos antes de mirar la solución.
Problema Propuesto 1
Encuentra la ecuación de una parábola con vértice en el origen y cuyo foco está ubicado en el punto \( F(-5, 0) \).
Haz clic aquí para ver la solución
Análisis: Como el foco tiene coordenadas \( (-5, 0) \), notamos que el valor se mueve en el eje X, por lo tanto es Horizontal.
El valor de \( p \) es directamente la coordenada del foco: \( p = -5 \).
Sustituimos en \( y^2 = 4px \):
\[ y^2 = 4(-5)x \]
\[ \boldsymbol{y^2 = -20x} \]
Es una parábola horizontal que abre hacia la izquierda.
Problema Propuesto 2
Una parábola tiene su vértice en el origen y su directriz es la recta \( y - 2 = 0 \). Hallar su ecuación.
Haz clic aquí para ver la solución
Análisis: Primero despejamos la directriz: \( y = 2 \).
Al ser una recta del tipo "y = constante", sabemos que es una directriz horizontal, lo que implica que la parábola es Vertical.
La fórmula de la directriz vertical es \( y = -p \).
Si \( y = 2 \), entonces:
\[ -p = 2 \quad \Rightarrow \quad p = -2 \]
Sustituimos en \( x^2 = 4py \):
\[ x^2 = 4(-2)y \]
\[ \boldsymbol{x^2 = -8y} \]
Es una parábola vertical que abre hacia abajo.
🚀 ¡Excelente Trabajo! ¿Cuál es el siguiente paso?
¡Felicidades! Has dominado los conceptos básicos de la Parábola con Vértice en el Origen. Ahora eres capaz de identificar su orientación solo con ver la ecuación y calcular todos sus elementos geométricos.
Sin embargo, el mundo real no siempre es tan ordenado. ¿Qué pasa cuando la parábola se desplaza y el vértice ya no está en (0,0)? Este tema es una pieza clave de nuestro artículo pilar sobre Geometría Analítica. Te recomendamos visitar el siguiente nivel para convertirte en un experto total.
¿Te gustó este contenido?
Únete a nuestra comunidad en WhatsApp o Telegram para recibir nuevos proyectos, tutoriales y noticias exclusivas.
-
Me pueden ayudar a encontrar los elementos de la parabola con vertice en el origen cuya ecuación es x² + 38y =0
-
muy bueno me ayudo a mi exposicion excelente servicio gracias
-
Ire nomas, ayudando a salvar el semestre. Bien explicado :^)
10 Deja tu comentario
Deja una respuesta

Estos temas te pueden interesar