Ecuación de la Recta en su forma simétrica

Hoy veremos un nuevo tema de nuestros artículos sobre geometría analítica, y se trata sobre el tema de la ecuación de la recta en su forma simétrica o canónica, pues bien, hasta este punto de nuestras publicaciones de ejercicios y problemas de la recta, hemos estudiado tres formas, las cuales se mencionan a continuación:

1. Ecuación de la Recta en su forma Punto - Pendiente
2. Ecuación de la Recta dado dos Puntos
3. Ecuación de la Recta Pendiente - Ordenada al Origen

Ahora toca el caso para el último caso que estudiaremos en el blog, y se trata sobre la ecuación simétrica o canónica de la recta.

Obtención de la fórmula de la ecuación de la Recta en su forma simétrica

La fórmula es la siguiente:

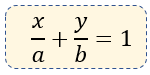
¿Cómo la obtenemos??

Para obtener la fórmula de la recta, veamos la siguiente gráfica. Donde tenemos una recta "L" que intersecta a los ejes "x" y "y" en los puntos A (a,0) y B (0,b), respectivamente. Tal como se ilustra en la gráfica:

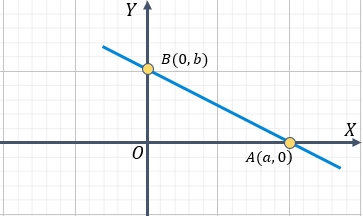
Las coordenadas que tenemos, son las siguientes:

$\displaystyle {{x}_{1}}=a$

$\displaystyle {{y}_{1}}=0$

$\displaystyle {{x}_{2}}=0$

$\displaystyle {{y}_{2}}=b$

Si deseamos encontrar la pendiente de la recta, tenemos que utilizar la fórmula de la pendiente.

$\displaystyle m=\frac{{{y}_{1}}-{{y}_{2}}}{{{x}_{1}}-{{x}_{2}}}$

Al sustituir en nuestros datos en la fórmula:

$\displaystyle m=\frac{{{y}_{1}}-{{y}_{2}}}{{{x}_{1}}-{{x}_{2}}}=\frac{0-b}{a-0}=-\frac{b}{a}$

Es decir:

$\displaystyle m=-\frac{b}{a}$

Ahora procedemos a utilizar la fórmula de la ecuación punto - pendiente:

$\displaystyle y-{{y}_{1}}=m(x-{{x}_{1}})$

Sustituimos nuestros datos en dicha fórmula:

$\displaystyle y-0=-\frac{b}{a}(x-a)$

Simplificando . . .

$\displaystyle y=-\frac{bx}{a}+b$

Multiplicando toda la ecuación por "a", obtenemos:

$\displaystyle a\left( y \right)=a\left( -\frac{bx}{a}+b \right)$

Obtenemos

$\displaystyle ay=-bx+ab$

Vamos a dividir la ecuación por "ab":

$\displaystyle \frac{ay}{ab}=\frac{-bx+ab}{ab}$

Obtenemos

$\displaystyle \frac{y}{b}=-\frac{x}{a}+1$

Despejando a la unidad, es decir a "1" . Nos queda:

$\displaystyle \frac{y}{b}+\frac{x}{a}=1$

Ordenando, finalmente tenemos:

$\displaystyle \frac{x}{a}+\frac{y}{b}=1$

? Finalmente encontramos la ecuación que también se le conoce como reducida o de abscisa.

Ejercicios Resueltos sobre la forma simétrica de la ecuación de la Recta

Veamos algunos ejemplos resueltos.

Solución:

Al ver los datos del problema, podemos decir que: a = 3, y b = -4 . Entonces solamente tenemos que sustituir estos datos en nuestra fórmula.

$\displaystyle \frac{x}{a}+\frac{y}{b}=1$

Sustituyendo

$\displaystyle \frac{x}{3}+\frac{y}{-4}=1$

El - 4 debajo de "y", hará que se vuelva negativa.

$\displaystyle \frac{x}{3}-\frac{y}{4}=1$

Para eliminar a los denominadores que tenemos, podemos multiplicar toda la ecuación por 12.

$\displaystyle 12\left( \frac{x}{3}-\frac{y}{4} \right)=12\left( 1 \right)$

Esto nos dará:

$\displaystyle 4x-3y=12$

Una vez simplificada la ecuación. Vamos a igualar a cero.

Resultado:

$\displaystyle 4x-3y-12=0$

Gráficamente la ecuación de la recta, es la siguiente:

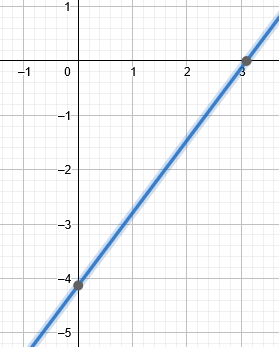
Solución:

Al sustituir los datos que tenemos, sabemos que a = -2 y b = 6 ; por lo que:

$\displaystyle \frac{x}{a}+\frac{y}{b}=1$

Sustituyendo

$\displaystyle \frac{x}{-2}+\frac{y}{6}=1$

Qué es igual a :

$\displaystyle -\frac{x}{2}+\frac{y}{6}=1$

Multiplicando por 12 a toda la ecuación tenemos que:

$\displaystyle 12\left( -\frac{x}{2}+\frac{y}{6} \right)=12\left( 1 \right)$

Por lo que:

$\displaystyle -6x+2y=12$

Igualando la ecuación a cero:

Resultado:

$\displaystyle 6x-2y+12=0$

Dicha ecuación, la podemos observar gráficamente de la siguiente manera:

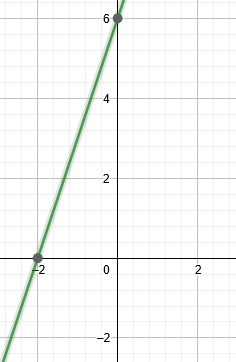
Solución:

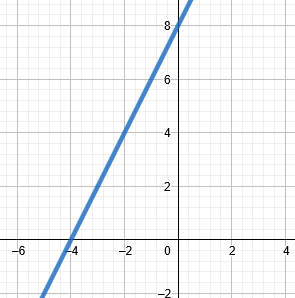
Los datos que tenemos son los siguientes, para a = -4 y b = 8. Con estos datos podemos resolver nuestro ejemplo sin dificultades.

$\displaystyle \frac{x}{a}+\frac{y}{b}=1$

Sustituyendo en la fórmula:

$\displaystyle \frac{x}{-4}+\frac{y}{8}=1$

Dicho de otra forma, esto es:

$\displaystyle -\frac{x}{4}+\frac{y}{8}=1$

Podemos multiplicar toda la ecuación por 8, y esto simplificará nuestros cálculos.

$\displaystyle 8\left( -\frac{x}{4}+\frac{y}{8} \right)=8\left( 1 \right)$

Obtenemos:

$\displaystyle -2x+y=8$

Igualando a cero:

$\displaystyle 8+2x-y=0$

Ordenando.

Resultado:

$\displaystyle 2x-y+8=0$

De forma gráfica, esto es: