Ecuación de la Recta Pendiente - Ordenada al origen

Dentro de nuestro estudio de Geometría Analítica, una vez que entendemos que la ecuación de la recta la podemos encontrar mediante un punto y pendiente, o cuando pasa por dos puntos. También tenemos el caso de la ecuación de la recta con los datos de la pendiente y la ordenada al origen (intersección con el eje "y" ) , se da por la siguiente ecuación:
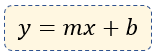
Es muy fácil obtener dicha ecuación, si consideramos que existe una recta L , cuya pendiente es "m" y pasa a través del punto B (0, b), entonces tenemos algo similar a la siguiente gráfica.
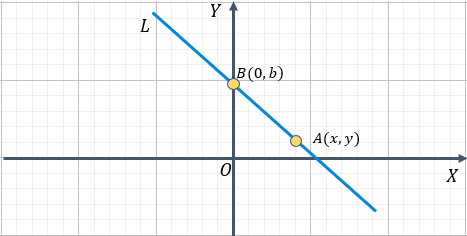
Asumiendo que la ecuación de la recta, teniendo un punto y pendiente es de la siguiente forma:
$\displaystyle y-{{y}_{1}}=m(x-{{x}_{1}})$
Si tenemos solamente un punto que es el punto B, cuyas coordenadas son (0,b); entonces podemos decir que:
$\displaystyle {{x}_{1}}=0$
$\displaystyle {{y}_{1}}=b$
De aquí sustituimos en la fórmula anterior y decimos que:
$\displaystyle y-b=m(x-0)$
Multiplicando en el segundo miembro:
$\displaystyle y-b=mx$
Despejando a "y", tenemos
$\displaystyle y=mx+b$
Qué es prácticamente, la forma reducida o simplificada de la recta. Ahora veamos algunos ejemplos para poner en práctica la ecuación de la recta pendiente - ordenada al origen.
Ejercicios de la Ecuación de la Recta Pendiente - Ordenada al origen
Solución:
Los datos que tenemos del problema, es tanto la pendiente: m= -2/7 y la ordenada al origen es b = 3.
Al sustituir nuestros datos, obtenemos:
$\displaystyle y=mx+b$
De aquí:
$\displaystyle y=-\frac{2}{7}x+3$
Multiplicando toda la ecuación por 7, para hacer más cómoda las operaciones. Obtenemos:
$\displaystyle 7\left( y \right)=7\left( -\frac{2}{7}x+3 \right)$
Tenemos que:
$\displaystyle 7y=-2x+21$
Igualando la ecuación a cero, obtenemos:

$\displaystyle 2x+7y-21=0$
Qué gráficamente, la podemos observar de la siguiente forma: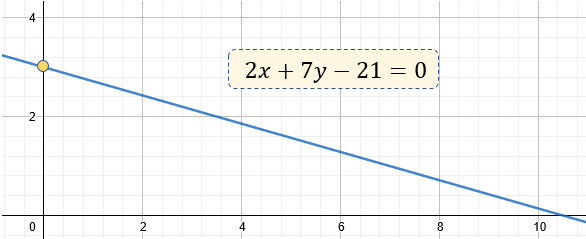
Solución:
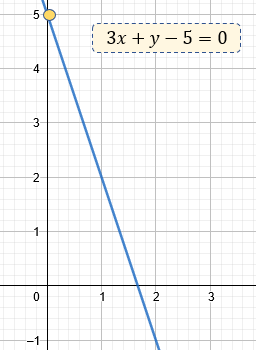
Para este caso, hacemos los pasos similares al ejemplo anterior. Buscamos nuestros datos, que suelen ser muy claro. Nuestra pendiente es m = -3, y nuestra ordenada al origen es b = 5. Pasamos estos datos a nuestra fórmula, y tenemos:
$\displaystyle y=mx+b$
Entonces:
$\displaystyle y=-3x+5$
Igualando a cero:
$\displaystyle y+3x-5=0$
Ordenando, obtenemos. Nuestro resultado:

$\displaystyle 3x+y-5=0$
Qué gráficamente, lo podemos observar como:
Solución:
Retomando los datos dados por el problema, sabemos que m = 2 y que b = -5/2. Sustituyendo estos valores en nuestra fórmula. Tenemos entonces que:
$\displaystyle y=mx+b$
Dónde:
$\displaystyle y=2x+\left( -\frac{5}{2} \right)$
Eliminando el paréntesis
$\displaystyle y=2x-\frac{5}{2}$
Multiplicando toda la ecuación por 2
$\displaystyle 2\left( y \right)=2\left( 2x-\frac{5}{2} \right)$
Quedando así:
$\displaystyle 2y=4x-5$
Igualando la ecuación a cero.

$\displaystyle 4x-2y-5=0$
Qué gráficamente, esto es.
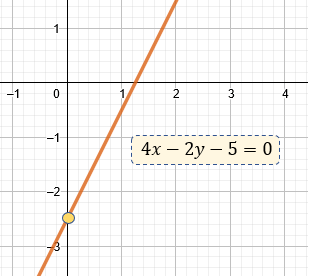
-
y=3/4x+1 m=3/2
-
muy didàctico los ejercicios
-
No entiendo bien, por que se multiplica por 2
-
En el último ejercicio porque se multiplica x 2
-
Para no tener fracciones (5/2) y facilitar las operaciones.
-
para quitarle el denominador a la fraccion de la ecuacion
-
7 Deja tu comentario
Deja una respuesta

Estos temas te pueden interesar