Ecuación de la Recta que pasa por dos puntos dados

Dentro de la Ecuación de la Recta , tenemos el caso de la Ecuación de la Recta que pasa por dos puntos dados , esto a diferencia del tema de la ecuación de la recta punto - pendiente, suelen ser muy similares, a diferencia que tenemos un punto más que hará que nuestra fórmula tenga un aspecto diferente, y aunque no sea muy distinta, se aprecia de la siguiente forma:
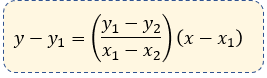
Por geometría se dice que podemos encontrar perfectamente la ecuación, si poseemos dos de sus puntos. Algunos autores le conocen a esta ecuación, como cartesiana.
Ecuación de la Recta dado dos puntos
Para entender mucho mejor nuestra fórmula, veamos gráficamente a que nos referimos.
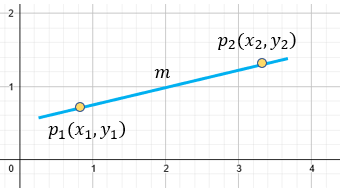
Ante nuestra ecuación, es importante indicar que debemos evitar que el denominador sea cero, por lo que es necesario que:
$latex \displaystyle {{x}_{2}}\ne {{x}_{1}}$
Ahora, para entender mucho mejor este tema, veamos los siguientes ejercicios resueltos.
Ejercicios Resueltos de Ecuación de la Recta dado dos puntos
Solución:
Para poder darle solución al problema, se resuelve de manera similar al caso del punto - pendiente, simplemente que aquí encontraremos nuestra pendiente a través de los dos puntos, ahora solo necesitamos sustituir nuestros datos en la fórmula.
Para hacerlo más sencillo aún, vamos a poner nuestros datos. Los que tenemos hasta ahora.
$latex \displaystyle {{x}_{1}}=-3$
$latex \displaystyle {{y}_{1}}=-1$
$latex \displaystyle {{x}_{2}}=5$
$latex \displaystyle {{y}_{2}}=2$
Ahora sustituimos en la fórmula:
$latex \displaystyle y-(-1)=\left( \frac{-1-2}{-3-5} \right)\left( x-(-3) \right)$
Resolviendo las operaciones indicadas
$latex \displaystyle y+1=\left( \frac{-3}{-8} \right)(x+3)$
Simplificando aún más
$latex \displaystyle y+1=\left( \frac{3}{8} \right)(x+3)$
Pasando el 8 a multiplicar lo del primer miembro, tenemos:
$latex \displaystyle 8(y+1)=3(x+3)$
Multiplicando
$latex \displaystyle 8y+8=3x+9$
Igualando la ecuación a cero.

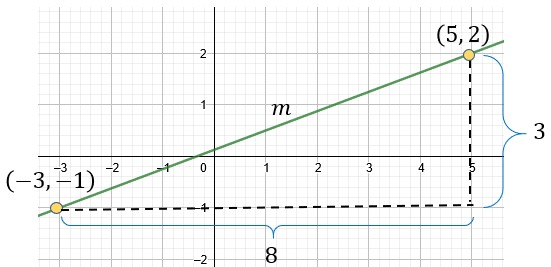
$latex \displaystyle 3x-8y+1=0$
De forma gráfica tenemos:
Solución:
Nuevamente, tenemos que colocar nuestros datos y a partir de ahí, empezar a sustituir en la fórmula, de la siguiente forma:
$latex \displaystyle {{x}_{1}}=-2$
$latex \displaystyle {{y}_{1}}=-1$
$latex \displaystyle {{x}_{2}}=-10$
$latex \displaystyle {{y}_{2}}=-5$
Vamos a sustituir estos datos, en nuestra fórmula.
$latex \displaystyle y-(-1)=\left( \frac{-1-(-5)}{-2-(-10)} \right)\left( x-(-2) \right)$
Realizando las operaciones indicadas
$latex \displaystyle y+1=\left( \frac{-1+5}{-2+10} \right)\left( x+2 \right)$
Simplificando
$latex \displaystyle y+1=\left( \frac{4}{8} \right)\left( x+2 \right)$
Luego
$latex \displaystyle 8(y+1)=4(x+2)$
Aplicando propiedad distributiva
$latex \displaystyle 8y+8=4x+8$
Igualando a cero

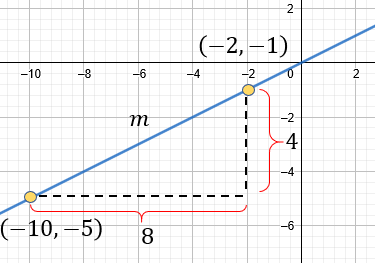
$latex \displaystyle 4x-8y=0$
De forma gráfica, tenemos:
-
2.- Calcula la ecuación de la recta que pasa por el punto A(-3,0) y tiene una
у
pendiente de 0. -
A(-4,1) B(3,-5) cual es el resultado
-
GRACIAS POR RESOLVER EL EJERCICIO?
-
me interesaria ver como resuelve un ejercicio donde p2(-5/2,8) y el p1(-3,4/3) porque trate de realizar los mismos pasos y no logre un resultado q me convenciera por favor y gracias
-
De la forma explicita te quedaria y= 40/3x + 124/3
-
-
muy buena explicación
8 Deja tu comentario
Deja una respuesta

Estos temas te pueden interesar