Resistividad – Ejercicios Resueltos

Carlos julián Física 20 comentarios

Después de más de un mes sin publicar contenido en el blog, volvemos a colocarnos las pilas y bien recargadas para traer más ejemplos resueltos de ejercicios, y es ahora como vamos a iniciar hablando de un tema que sin duda es de vital importancia para quienes estudian las leyes eléctricas. 😀

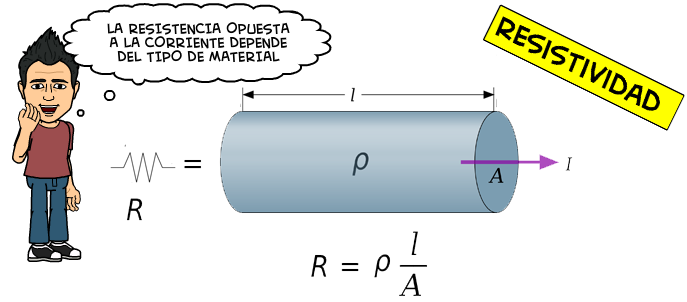
Hoy tocaremos el tema de la resistividad, este tema se basa en el comportamiento de la resistencia de un material, ya que el flujo de carga que pasa a través de éste siempre se topará con una fuerza opuesta a que esta fluya de tal manera que la podemos relacionar como una fricción mecánica, a esta oposición la conocemos como resistencia. Sin embargo cada material tiene su propia resistencia. 😎

En la ley del ohm no nos importaba saber de donde obteníamos los valores para las resistencias, y en este tema SI!!

Hay cuatro factores que tomaremos en cuenta para darle valores, que son:

Tipo de Material
Longitud
Área Transversal
Temperatura

La ecuación que usaremos para poder encontrar esos valores de resistencia con esas variables, será:

$\displaystyle R=\rho \frac{l}{A}$

Dónde:

$\displaystyle R$ = Resistividad ( $\displaystyle \Omega$ )

$\displaystyle \rho$ = Coeficiente de Resistividad ( $\displaystyle \Omega m$ )

$\displaystyle l$ = Longitud (m)

$\displaystyle A$ = Área ( $\displaystyle {{m}^{2}}$ )

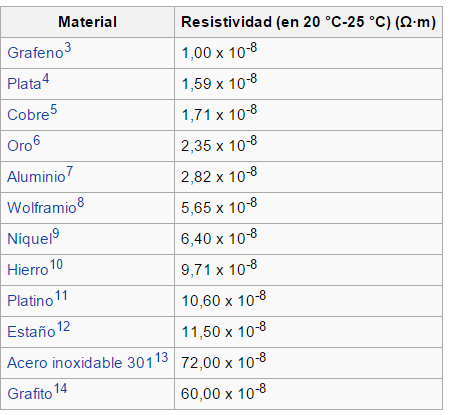
Existen tablas de resistividad eléctrica de algunos materiales que han sido tomados a una temperatura ambiente entre (20 C° – 25° C) celcius.

Ejercicios resueltos de Resistividad

Ahora pasemos a resolver unos ejemplos resueltos del tema de resistividad, para poder comprender a fondo podemos enfrentarnos a problemas como éstos.

1.- Determine la resistencia de 2400 cm de alambre de plata que posee un diámetro de 25 centímetros.

Solución: Para poder resolver el ejercicio, vamos a reunir nuestros datos sabiendo que nos piden la resistencia de un alambre de plata, por lo que:

$\displaystyle \rho =1.59x{{10}^{-8}}\Omega m$ (resistividad).

$\displaystyle l=2400cm\left( \frac{1m}{100cm} \right)=24m$

$\displaystyle d=25cm\left( \frac{1m}{100cm} \right)=0.25m$ (diámetro)

$\displaystyle A=\pi {{r}^{2}}=\pi {{\left( 0.125m \right)}^{2}}=0.04908{{m}^{2}}$

Reemplazando estos valores en nuestra fórmula:

$\displaystyle R=\rho \frac{l}{A}$

$\displaystyle R=1.59x{{10}^{-8}}\Omega m\left( \frac{24m}{0.04908{{m}^{2}}} \right)=7.775x{{10}^{-6}}\Omega$

2.- Un conductor de 30m de largo y 20 ohm de resistencia tiene una resistividad de 2,63.10 elevado a – 8 ohm-m ¿Cual es el diámetro de dicho conductor?.

Solución: Este es un problema un poco más complicado que el anterior, debido a que en este caso tenemos que despejar una variable de nuestra fórmula:

$\displaystyle R=\rho \frac{l}{A}$

De aquí despejaremos al Área (A).

$\displaystyle A=\rho \frac{l}{R}$

Tenemos los datos de la longitud del conductor, la resistividad y el valor de la resistencia, por lo que lo único que nos queda es reemplazar esos datos en la fórmula.

$\displaystyle A=(2.63x{{10}^{-8}}\Omega m)\frac{30m}{20\Omega }$

$\displaystyle A=3.945x{{10}^{-8}}{{m}^{2}}$

Qué sería el área del conductor. 😀

Recordemos que el diámetro lo podemos calcular, por la fórmula del área:

$\displaystyle A=\frac{\pi {{d}^{2}}}{4}$

despejando a “d”, nos queda:

$\displaystyle d=\sqrt{\frac{4A}{\pi }}$

sustituyendo en nuestros datos:

$\displaystyle d=\sqrt{\frac{4A}{\pi }}=\sqrt{\frac{4(3.945x{{10}^{-8}})}{\pi }}=2.24x{{10}^{-4}}m$

Por lo que nuestro diámetro es de:

$\displaystyle d=2.24x{{10}^{-4}}m$

Ahora vamos a resolver un ejercicio que nos envío un suscriptor del blog.

3.- ¿Qué diámetro debe tener un alambre de cobre si su resistencia ha de ser la misma que la de uno de aluminio de la misma longitud con diámetro de 3.26 mm?

Solución: Este es un problema que implica un análisis más profundo que los dos ejemplos anteriores, primero porque se involucran dos materiales, y la otra, porque realmente aplicamos algunos conceptos matemáticos para hacernos más fácil la solución.

Ambos materiales tienen la misma longitud, por lo cual no hace falta representarla en nuestra fórmula, es decir;

$\displaystyle {{R}_{Al}}={{R}_{Cu}}$ (Porque ambas tienen la misma resistencia)

$\displaystyle {{\rho }_{Al}}\frac{l}{A}={{\rho }_{Cu}}\frac{l}{A}$ (Igualamos ecuaciones)

$\displaystyle \frac{{{\rho }_{Al}}}{A}=\frac{{{\rho }_{Cu}}}{A}$ (Quitamos la longitud ya que son la misma)

Cálculo para el Aluminio

$\displaystyle {{\rho }_{Al}}=2.82x{{10}^{-8}}\Omega m$

$\displaystyle \varnothing =3.26x{{10}^{-3}}m$ (diámetro)

Vamos a calcular el área de este conductor, sabiendo su diámetro podemos hacerlo de la siguiente forma.

$\displaystyle A=\frac{\pi {{d}^{2}}}{4}=\frac{\pi {{\left( 3.26x{{10}^{-3}}m \right)}^{2}}}{4}=8.3469x{{10}^{-6}}{{m}^{2}}$

Ahora realizaremos lo mismo con el cobre.

Cálculo para el Cobre

$\displaystyle {{\rho }_{Cu}}=1.71x{{10}^{-8}}\Omega m$

En el caso del cobre, no tenemos el área porque justamente el problema nos pide el diámetro, entonces tendremos que despejar nuestra fórmula al área, para trabajarlo desde ahí.

$\displaystyle {{A}_{Cu}}=\frac{{{\rho }_{Cu}}\cdot {{A}_{Al}}}{{{\rho }_{Al}}}$

Reemplazando nuestros datos en la fórmula, tenemos:

$\displaystyle {{A}_{Cu}}=\frac{{{\rho }_{Cu}}\cdot {{A}_{Al}}}{{{\rho }_{Al}}}=\frac{(1.71x{{10}^{-8}}\Omega m)(8.3469x{{10}^{-6}}{{m}^{2}})}{2.82x{{10}^{-8}}\Omega m}=5.06x{{10}^{-6}}{{m}^{2}}$

Ya obtuvimos nuestra área, sin embargo recordemos nuevamente que el problema nos pide el diámetro, entonces sabiendo que de la fórmula de la circunferencia podemos obtener el diámetro, esto nos queda.

$\displaystyle A=\,\frac{\pi {{d}^{2}}}{4}$

$\displaystyle \sqrt{\frac{4A}{\pi }}=\,d$

Ordenando …

$\displaystyle d=\sqrt{\frac{4A}{\pi }}$

Sustituyendo valores.

$\displaystyle d=\sqrt{\frac{4(5.06x{{10}^{-6}}{{m}^{2}})}{\pi }}=2.53x{{10}^{-3}}m=2.53mm$

Por lo que el diámetro de la sección del conductor es de $\displaystyle 2.53x{{10}^{-3}}m$

Por lo que con esto se concluye el ejercicio 😎

Si este post te ha servido, no dudes en compartirlo en tus redes sociales. !!!

Acerca del Autor

Carlos julián

Fundador de Fisimat, Desarrollador Web y Profesor.

20 Comentarios

Daniel
agosto 31, 2015 | Responder
te hicieron falta pasos en el segundo ejercicio, ya que el resultado que presentas no es el el del diámetro sino el del área de la sección. Para obtener el diámetro habría que dividir entre (pi) y después sacar raíz cuadrada y luego multiplicarlo por 2 resultando 2.2411×10-4 m .00022411 m de diámetro

Carlos julián
agosto 31, 2015 | Responder
Es cierto Daniel, no nos habíamos percatado de ello.
Gracias por el aviso.
Saludos

Napo
noviembre 8, 2015 | Responder
el cálculo del área del Cu esta mal, el valor es 5,061 por diez a -6

Carlos julián
noviembre 8, 2015 | Responder
Ocurre que no tenemos un valor exacto para dicha resistividad, pero puedes sustituir la que tienes, y no pasa nada 🙂

Francisco
marzo 8, 2016 | Responder
Por qué divides el área del circulo sobre 4? Es lo único que no entendí, gracias.

Carlos julián
marzo 8, 2016 | Responder
Se divide sobre cuatro, porque es la fórmula del área, recuerda que podemos escribirla de muchas formas.
$\displaystyle A=\pi {{r}^{2}}$
Pero recuerda que el radio es igual a la mitad del diámetro, entonces podemos decir que:
$\displaystyle r=\frac{d}{2}$
Sustituyendo en la fórmula del área, tenemos.
$\displaystyle A=\pi {{\left( \frac{d}{2} \right)}^{2}}=\frac{\pi {{d}^{2}}}{4}$
De ahí es donde sale la fórmula:
$\displaystyle A=\frac{\pi {{d}^{2}}}{4}$
Saludos.

CHAVARRIA77
junio 9, 2016 | Responder
entonces en dado caso estabas sacando el valor del diametro en vez de el del radio, osea que ese resultado (2.24×10-4) tendrias que dividirlo entre 2
¿ó estoy mal?

Carlos julián
junio 11, 2016 | Responder
Si lo que quiero es radio, tendría que dividir ese diámetro en dos.

Marcela Ramos
septiembre 4, 2016 | Responder
Hola , una pregunta cual es la resistencia de un alambre conductor de cobre p=1,7*10 elevado a-8 ohm*m de 2 metros de largo y un mm de diametro?
eduardo
septiembre 10, 2016 | Responder
hola… me podrías ayudar con este ejercicio? Un conductor con una temperatura inicial de 18°c aumenta su temperatura en 4°.Su resistencia inicial R1 es de 11ohmios quedando con una resistencia final igual a 1,15 R1. Determinar su coeficiente de resistividad.
Selene
octubre 20, 2016 | Responder
Como puedo sacar la longitud?
Alejandro
diciembre 8, 2016 | Responder
disculpa cuando te dan el dato de masa del objeto por ejemplo masa del cobre, de que manera te ayuda para resolver un problema de resistencia.(porque en la formula no aparece nada de masas)
r.r
junio 25, 2017 | Responder
cual es la resistividad del hierro
r.r
junio 25, 2017 | Responder
?
Mario Platero
noviembre 10, 2017 | Responder
Saludos, en el problema 3 existe un error de calculo en el área del cobre, la respuesta debe de ser 5.0614×10^-6 m2. Quedando como respuesta final d=2.53mm

Carlos julián
noviembre 17, 2017 | Responder
Se ha corregido Mario, Gracias!! Saludos 😀

Fidel
marzo 13, 2018 | Responder
Hola tengo una grand duda. En un problema que me dejaron me. Piden calcular la longitud de un hilo conductor de fierro-níquel de 2.6mm de diámetro y 500 ohms de resistencia, la resistividad es de 0.8 y el resultado es 3318.3 m
armando
abril 10, 2018 | Responder
me parece un buen aporte
armando
abril 10, 2018 | Responder
me parece un excelente aporte
armando
abril 10, 2018 | Responder
te felicito

Ejercicios resueltos de Resistividad

Artículos Relacionados

Acerca del Autor

Carlos julián

Deja un comentario Cancelar respuesta