Resistividad - Ejercicios Resueltos
Después de más de un mes sin publicar contenido en el blog, volvemos a colocarnos las pilas y bien recargadas para traer más ejemplos resueltos de ejercicios, y es ahora como vamos a iniciar hablando de un tema que sin duda es de vital importancia para quienes estudian las leyes eléctricas. 😀
Hoy tocaremos el tema de la resistividad, este tema se basa en el comportamiento de la resistencia de un material, ya que el flujo de carga que pasa a través de éste siempre se topará con una fuerza opuesta a que esta fluya de tal manera que la podemos relacionar como una fricción mecánica, a esta oposición la conocemos como resistencia. Sin embargo cada material tiene su propia resistencia. 😎
En la ley del ohm no nos importaba saber de donde obteníamos los valores para las resistencias, y en este tema SI!!
Hay cuatro factores que tomaremos en cuenta para darle valores, que son:
- Tipo de Material
- Longitud
- Área Transversal
- Temperatura
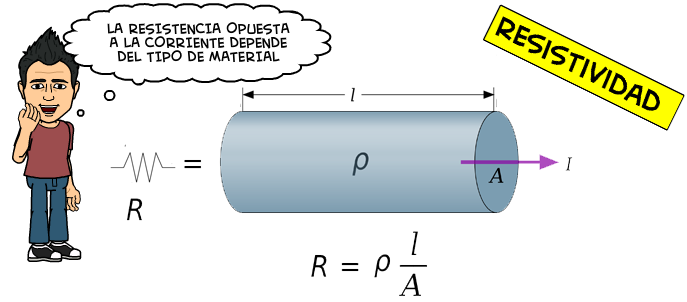
La ecuación que usaremos para poder encontrar esos valores de resistencia con esas variables, será:
$\displaystyle R=\rho \frac{l}{A}$
Dónde:
$\displaystyle R$ = Resistividad ($\displaystyle \Omega $)
$\displaystyle \rho $ = Coeficiente de Resistividad ($\displaystyle \Omega m$)
$\displaystyle l$ = Longitud (m)
$\displaystyle A$ = Área ($\displaystyle {{m}^{2}}$)
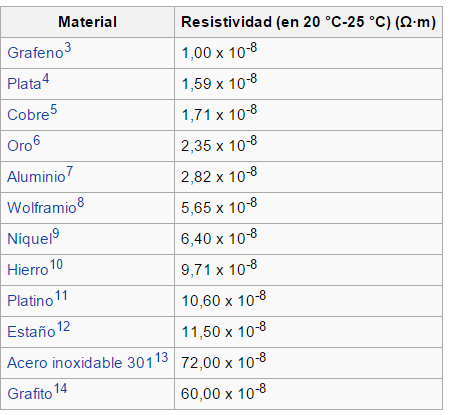
Existen tablas de resistividad eléctrica de algunos materiales que han sido tomados a una temperatura ambiente entre (20 C° - 25° C) celcius.
Ejercicios resueltos de Resistividad
Ahora pasemos a resolver unos ejemplos resueltos del tema de resistividad, para poder comprender a fondo podemos enfrentarnos a problemas como éstos.
Solución: Para poder resolver el ejercicio, vamos a reunir nuestros datos sabiendo que nos piden la resistencia de un alambre de plata, por lo que:
$\displaystyle \rho =1.59x{{10}^{-8}}\Omega m$ (resistividad).
$\displaystyle l=2400cm\left( \frac{1m}{100cm} \right)=24m$
$\displaystyle d=25cm\left( \frac{1m}{100cm} \right)=0.25m$ (diámetro)
$\displaystyle A=\pi {{r}^{2}}=\pi {{\left( 0.125m \right)}^{2}}=0.04908{{m}^{2}}$
Reemplazando estos valores en nuestra fórmula:
$\displaystyle R=\rho \frac{l}{A}$
$\displaystyle R=1.59x{{10}^{-8}}\Omega m\left( \frac{24m}{0.04908{{m}^{2}}} \right)=7.775x{{10}^{-6}}\Omega $
Solución: Este es un problema un poco más complicado que el anterior, debido a que en este caso tenemos que despejar una variable de nuestra fórmula:
$\displaystyle R=\rho \frac{l}{A}$
De aquí despejaremos al Área (A).
$\displaystyle A=\rho \frac{l}{R}$
Tenemos los datos de la longitud del conductor, la resistividad y el valor de la resistencia, por lo que lo único que nos queda es reemplazar esos datos en la fórmula.
$\displaystyle A=(2.63x{{10}^{-8}}\Omega m)\frac{30m}{20\Omega }$
$\displaystyle A=3.945x{{10}^{-8}}{{m}^{2}}$
Qué sería el área del conductor. 😀
Recordemos que el diámetro lo podemos calcular, por la fórmula del área:
$\displaystyle A=\frac{\pi {{d}^{2}}}{4}$
despejando a "d", nos queda:
$\displaystyle d=\sqrt{\frac{4A}{\pi }}$
sustituyendo en nuestros datos:
$\displaystyle d=\sqrt{\frac{4A}{\pi }}=\sqrt{\frac{4(3.945x{{10}^{-8}})}{\pi }}=2.24x{{10}^{-4}}m$
Por lo que nuestro diámetro es de:
$\displaystyle d=2.24x{{10}^{-4}}m$
Ahora vamos a resolver un ejercicio que nos envío un suscriptor del blog.
Solución: Este es un problema que implica un análisis más profundo que los dos ejemplos anteriores, primero porque se involucran dos materiales, y la otra, porque realmente aplicamos algunos conceptos matemáticos para hacernos más fácil la solución.
Ambos materiales tienen la misma longitud, por lo cual no hace falta representarla en nuestra fórmula, es decir;
$\displaystyle {{R}_{Al}}={{R}_{Cu}}$ (Porque ambas tienen la misma resistencia)
$\displaystyle {{\rho }_{Al}}\frac{l}{A}={{\rho }_{Cu}}\frac{l}{A}$ (Igualamos ecuaciones)
$\displaystyle \frac{{{\rho }_{Al}}}{A}=\frac{{{\rho }_{Cu}}}{A}$ (Quitamos la longitud ya que son la misma)
Cálculo para el Aluminio
$\displaystyle {{\rho }_{Al}}=2.82x{{10}^{-8}}\Omega m$
$\displaystyle \varnothing =3.26x{{10}^{-3}}m$ (diámetro)
Vamos a calcular el área de este conductor, sabiendo su diámetro podemos hacerlo de la siguiente forma.
$\displaystyle A=\frac{\pi {{d}^{2}}}{4}=\frac{\pi {{\left( 3.26x{{10}^{-3}}m \right)}^{2}}}{4}=8.3469x{{10}^{-6}}{{m}^{2}}$
Ahora realizaremos lo mismo con el cobre.
Cálculo para el Cobre
$\displaystyle {{\rho }_{Cu}}=1.71x{{10}^{-8}}\Omega m$
En el caso del cobre, no tenemos el área porque justamente el problema nos pide el diámetro, entonces tendremos que despejar nuestra fórmula al área, para trabajarlo desde ahí.
$\displaystyle {{A}_{Cu}}=\frac{{{\rho }_{Cu}}\cdot {{A}_{Al}}}{{{\rho }_{Al}}}$
Reemplazando nuestros datos en la fórmula, tenemos:
$\displaystyle {{A}_{Cu}}=\frac{{{\rho }_{Cu}}\cdot {{A}_{Al}}}{{{\rho }_{Al}}}=\frac{(1.71x{{10}^{-8}}\Omega m)(8.3469x{{10}^{-6}}{{m}^{2}})}{2.82x{{10}^{-8}}\Omega m}=5.06x{{10}^{-6}}{{m}^{2}}$
Ya obtuvimos nuestra área, sin embargo recordemos nuevamente que el problema nos pide el diámetro, entonces sabiendo que de la fórmula de la circunferencia podemos obtener el diámetro, esto nos queda.
$\displaystyle A=\,\frac{\pi {{d}^{2}}}{4}$
$\displaystyle \sqrt{\frac{4A}{\pi }}=\,d$
Ordenando ...
$\displaystyle d=\sqrt{\frac{4A}{\pi }}$
Sustituyendo valores.
$\displaystyle d=\sqrt{\frac{4(5.06x{{10}^{-6}}{{m}^{2}})}{\pi }}=2.53x{{10}^{-3}}m=2.53mm$
Por lo que el diámetro de la sección del conductor es de $\displaystyle 2.53x{{10}^{-3}}m$
Por lo que con esto se concluye el ejercicio 😎
Si este post te ha servido, no dudes en compartirlo en tus redes sociales. !!!
-
Hola , una pregunta cual es la resistencia de un alambre conductor de cobre p=1,7*10 elevado a-8 ohm*m de 2 metros de largo y un mm de diametro?
-
La resistencia es igual R=4.331×10^-3 ohm
-
saludo me pueden ayudar con este ejercicio. Encuentra la resistencia en un material que tiene forma de un cuadrado y uno de sus lados mide 2 cm, además, el largo es de 20 metros u por último su resistividad es de 1000 π* cm.
-
se que ya es tarde pero el resultado no sería: 0.4331*10^-2?
ya que a la hora de dividir:
3.4*10^-8 / 7.85 * 10^-7= 0.4331* 10^-1
Es decir: 4.331 * 10 ^-2 -
perdón quise decir 4.331*10^-2 al principio
-
-
-
entonces en dado caso estabas sacando el valor del diametro en vez de el del radio, osea que ese resultado (2.24x10-4) tendrias que dividirlo entre 2
¿ó estoy mal? -
Por qué divides el área del circulo sobre 4? Es lo único que no entendí, gracias.
-
lo que no consigo comprender es cuando tenemos que usar la formula del area--pi x dcuadrado/4 y la formula de s=pi por r cuadrado
os agradeceria mucho una respuesta a mi correo
gracias -
Un alambre tiene una resistencia nominal de 30 ohmios a 20°c según el manual del fabricante también se sabe que a 30°c su resistencia será de 33 ohmios cual será su resistencia a 38°c
-
-
el cálculo del área del Cu esta mal, el valor es 5,061 por diez a -6
-
te hicieron falta pasos en el segundo ejercicio, ya que el resultado que presentas no es el el del diámetro sino el del área de la sección. Para obtener el diámetro habría que dividir entre (pi) y después sacar raíz cuadrada y luego multiplicarlo por 2 resultando 2.2411x10-4 m .00022411 m de diámetro
79 Deja tu comentario
Deja una respuesta

Estos temas te pueden interesar