Energía Cinética Rotacional - Ejercicios Resueltos
Amigos de Fisimat, hoy hablaremos sobre la Energía Cinética Rotacional, ¿alguna vez te has preguntado por qué una pelota que rueda por una pendiente llega más lejos que una que simplemente se desliza? ¿o por qué un trompo sigue girando incluso después de que lo lanzaste? más allá del simple movimiento lineal, los objetos que giran almacenan energía de una forma impresionante, en la que influyen en gran cantidad de fenómenos que nos rodean.
Es importante que antes de comenzar este tema de Física sepas que todo está relacionado directamente con los temas de momento de inercia y momento angular. Es importante que los tengas en cuenta para abordar mejor el tema e incluso comprendas mejor los ejercicios propuestos, pero primero respondamos a la pregunta ¿qué es la energía cinética rotacional?.
¿Qué es la Energía Cinética Rotacional?
Cualquier objeto en movimiento posee energía cinética. Sabemos incluso como calcularla (para un cuerpo que experimenta movimiento traslacional), pero ¿qué sucede con un cuerpo rígido que está rotando?. Esto podría parecer complicado de entender, ya que cada punto en el cuerpo rígido posee una velocidad diferente. Sin embargo, podemos hacer uso de la velocidad angular (que es la misma para todo el cuerpo rígido) para expresar la energía cinética del objeto en rotación, pero lo veamos con un ejemplo real. Observemos la imagen:
En la imagen vemos a una persona con un esmeril, el esmeril es una máquina rotativa con mucha energía impulsada por un motor, en la imagen se logran ver las chispas, por lo general ruido y vibraciones mientras realizan un trabajo. Este sistema tiene una cantidad considerable de energía, parte de ella en forma de calor, luz, sonido y vibraciones. Sin embargo, la mayor parte de esta energía está en forma de energía cinética rotacional.
La energía en el movimiento rotacional es una forma de energía cinética asociada con la rotación, similar a la energía cinética traslacional. Para un cuerpo rígido en rotación, se puede expresar en términos de la velocidad angular (ω) que es constante para todos los puntos del cuerpo. Esto se logra relacionando ω con la velocidad tangencial $\displaystyle {{v}_{t}}$ mediante la fórmula $\displaystyle {{v}_{t}}=\omega r$ , donde r es la distancia al eje de rotación. Este enfoque simplifica mucho el cálculo de la energía cinética rotacional, veamos entonces como nos quedaría matemáticamente:
$\displaystyle {{E}_{c}}=\frac{1}{2}mv_{t}^{2}=\frac{1}{2}m{{(\omega r)}^{2}}=\frac{1}{2}\left( {m{{r}^{2}}} \right){{\omega }^{2}}$
Pero como sabemos que el momento de inercia tiene por ecuación:
$\displaystyle I=m{{r}^{2}}$
Sustituyendo, obtendríamos:
$\displaystyle K=\frac{1}{2}I{{\omega }^{2}}$
Fórmula de la Energía Cinética Rotacional
La energía cinética rotacional de un cuerpo tiene un valor igual al trabajo realizado por un momento de rotación resultante que de alguna forma acelera al cuerpo en su movimiento giratorio hasta que adquiere una velocidad final. Esta expresión se denota matematicamente como:
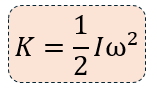
Ejercicios Resueltos de Energía Cinética Rotacional
Veamos algunos ejemplos resueltos sobre este tema:
Problema 1. Un disco uniforme de masa m = 2kg y radio r = 0.5m gira alrededor de su eje con una velocidad angular ω = 10 rad/s .Calcula la energía cinética rotacional del disco
Solución:
El momento de inercia de un disco girando alrededor de su eje es:
$\displaystyle I=\frac{1}{2}m{{r}^{2}}$
Sustituyendo los datos:
$\displaystyle I=\frac{1}{2}\left( {2kg} \right){{\left( {0.5m} \right)}^{2}}=0.25kg\cdot {{m}^{2}}$
Ahora calculamos la energía cinética rotacional:
$\displaystyle K=\frac{1}{2}\left( {0.25} \right){{\left( {10} \right)}^{2}}=12.5J$
Respuesta: Por lo tanto la energía cinética rotacional es de 12.5 J
Problema 2. Una esfera sólida de masa m = 4kg y radio r = 0.3m gira con una velocidad angular ω = 20 rad/s .Calcula su energía cinética rotacional.
Solución:
Para una esfera sólida, el momento de inercia es:
$\displaystyle I=\frac{2}{5}m{{r}^{2}}$
Sustituyendo los valores:
$\displaystyle I=\frac{2}{5}\left( {4kg} \right){{\left( {0.3m} \right)}^{2}}=0.144kg\cdot {{m}^{2}}$
La energía cinética rotacional es:
$\displaystyle K=\frac{1}{2}I{{\omega }^{2}}=\frac{1}{2}\left( {0.144kg{{m}^{2}}} \right){{\left( {20\frac{{rad}}{s}} \right)}^{2}}=28.8J$
Respuesta: Por lo que la energía cinética rotacional es de 28.8 J
Problema 3. Un cilindro hueco de masa m = 3kg y radio r = 0.4 m gira con ω = 15 rad/s. Determina su energía cinética rotacional.
Solución:
Para un cilindro hueco girando alrededor de su eje, el momento de inercia es:
$\displaystyle I=m{{r}^{2}}$
Sustituyendo los valores:
$\displaystyle I=m{{r}^{2}}=\left( {3kg} \right){{\left( {0.4m} \right)}^{2}}=0.48kg{{m}^{2}}$
La energía rotacional es:
$\displaystyle K=\frac{1}{2}I{{\omega }^{2}}=\frac{1}{2}\left( {0.48kg{{m}^{2}}} \right){{\left( {15\frac{{rad}}{s}} \right)}^{2}}=54J$
Respuesta: Por lo que la energía cinética rotacional es de 54 J
Problema 4. Una barra delgada de longitud L = 2m y masa m = 5kg gira alrededor de uno de sus extremos con una velocidad angular ω = 8 rad/s. Calcula su energía cinética rotacional.
Solución:
El momento de inercia de una barra delgada girando alrededor de un extremo es:
$\displaystyle I=\frac{1}{3}m{{L}^{2}}$
Sustituyendo:
$\displaystyle I=\frac{1}{3}m{{L}^{2}}=\frac{1}{3}\left( {5kg} \right){{\left( {2m} \right)}^{2}}\approx 6.67kg\cdot {{m}^{2}}$
La energía cinética rotacional es:
$\displaystyle K=\frac{1}{2}I{{\omega }^{2}}=\frac{1}{2}\left( {6.67kg{{m}^{2}}} \right){{\left( {8\frac{{rad}}{s}} \right)}^{2}}\approx 213.44J$
Respuesta: La energía cinética rotacional es aproximadamente 213.44 J
Deja una respuesta
Temas que podrían interesarte 👇