Fricción + Ejercicios Resueltos
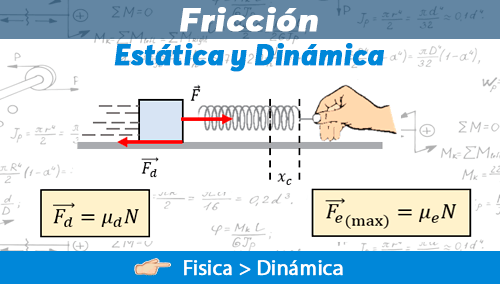
La fricción es un tema de gran relevancia en la Dinámica, una rama de la Física que se encarga a estudiar a los cuerpos en movimiento, para entender el tema de fricción es necesario que respondamos puntualmente ¿qué es la fricción?.
¿Qué es la Fricción?
Bajo la definición de muchos autores, la fricción o rozamiento es considerada como aquella fuerza que se opone al movimiento de cualquier objeto. Dicha fuerza es opuesta a su movimiento y se considera también una fuerza tangencial paralela a las superficies que están en contacto. Esta a su vez se divide en dos tipos de fricción, la fricción estática y la fricción dinámica.
Es muy importante considerar también que en la fricción estática la fuerza necesaria para poder mover al objeto será siempre mayor que la magnitud de la fricción dinámica, esto es porque se requiere de mucha más fuerza para lograr que un cuerpo inicie su movimiento.
Veamos el siguiente análisis
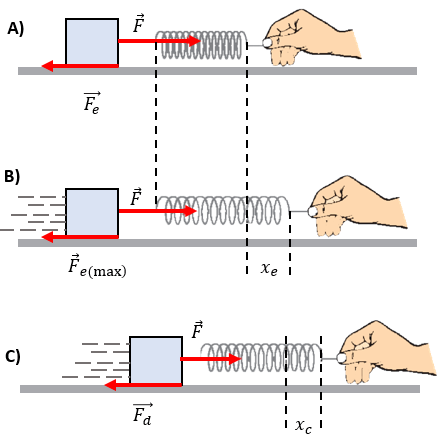
Analizando el punto A)
En el siguiente ejemplo se puede observar a un agente externo que aplica una Fuerza de empuje o estiramiento en el resorte que a su vez conecta con el bloque, dicha fuerza se encuentra con un problema, y es que para poder mover el objeto, necesita vencer a la fuerza estática, esta fuerza mantiene al bloque 'pegado' al suelo, y es una fuerza que actúa de forma contraria al movimiento. A lo largo de este blog, la vamos a considerar como Fuerza de Fricción Estática:
$\displaystyle \overrightarrow{{{F}_{e}}}$
Analizando el punto B)
Justo cuando la fuerza externa logra vencer a la fuerza estática, se experimenta una fuerza máxima estática , antes de que logre iniciar el movimiento el bloque. Esto es importante, porque vemos un instante tiempo donde la fuerza estática llega a un punto alto.
$\displaystyle {{\overrightarrow{F}}_{e(\max )}}$
Analizando el punto C)
En el punto C, observamos ya una fuerza de fricción dinámica, pues el objeto ya permanece en movimiento, aún así la fricción sigue ejerciendo una fuerza en sentido opuesto a la fuerza aplicada.
$\displaystyle \overrightarrow{{{F}_{d}}}$
De forma gráfica veríamos algo así:
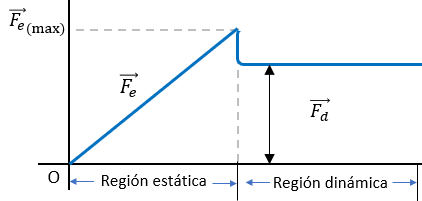
Fórmula para la Fuerza de Fricción Estática
La fórmula de fuerza de Fricción estática es la siguiente:
$\displaystyle {{\overrightarrow{{{F}_{e}}}}_{(\max )}}={{\mu }_{e}}N$
Donde:
$\displaystyle {{\overrightarrow{{{F}_{e}}}}_{(\max )}}$ = Fuerza de Fricción Máxima Estática (N)
$\displaystyle {{\mu }_{e}}$ = Coeficiente de Fricción Estática (adimensional)
$\displaystyle N$ = Normal (fuerza que tiende mantener unidas las superficies de contacto debido al peso).
Fórmula para la Fuerza de Fricción Dinámica
La fórmula de fricción dinámica es la siguiente:
$\displaystyle \overrightarrow{{{F}_{d}}}={{\mu }_{d}}N$
Donde:
$\displaystyle \overrightarrow{{{F}_{d}}}$ = Fuerza de fricción dinámica (N)
$\displaystyle {{\mu }_{d}}$ = Coeficiente de Fricción dinámico (adimensional)
$\displaystyle N$ = Normal (fuerza que mantiene unidas las superficies de contacto debido al peso).
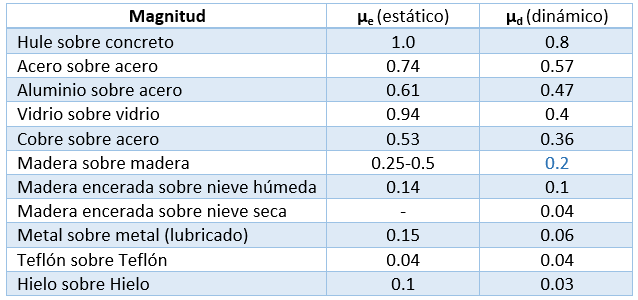
Coeficiente de Fricción de algunos elementos
Por lo general los valores de los coeficientes dependen de la naturaleza de las superficies. De la tabla podemos observar que:
$\displaystyle {{\mu }_{e}}>{{\mu }_{d}}$
Ejercicios Resueltos de Fricción
Para comprender mucho mejor el tema veamos algunos ejemplos o problemas resueltos de Fricción, y con ello entender mucho mejor este tema.
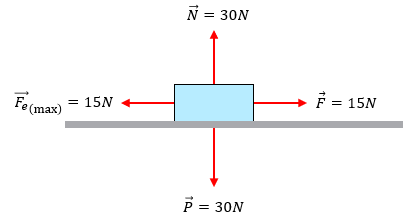
Solución:
Como lo que nos piden es prácticamente el coeficiente de rozamiento de fricción estática, solamente debemos recordar que en nuestra fórmula es la razón entre la fuerza estática máxima y la normal, dichos datos los tenemos:
$\displaystyle {{\mu }_{e}}=\frac{{{\overrightarrow{{{F}_{e}}}}_{(\max )}}}{N}=\frac{15N}{30N}=0.5$
Lo que vendría a ser nuestro coeficiente de fricción estático entre la madera y el acero.
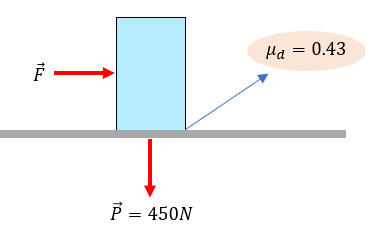
Solución:
En este caso nos proporcionan el coeficiente de fricción dinámico, además del peso del mueble, es lógico que tendremos que utilizar la fórmula de la fuerza de fricción dinámica (ya que es opuesta a la fuerza que jala el objeto).
Nota: El valor de la fuerza normal (N) actúa en dirección al peso, es por eso que la fuerza normal tendrá el mismo valor que el peso. Si el mueble estuviera en un plano inclinado, entonces el problema tendría más procedimientos, ya que tendríamos que descomponer en forma rectangular a los vectores del peso, para poder encontrar la normal.
Bueno asumiendo lo dicho anteriormente, tendríamos que aplicar nuestra fórmula:
$\displaystyle \overrightarrow{{{F}_{d}}}={{\mu }_{d}}N$
Sustituyendo datos:
$\displaystyle \overrightarrow{{{F}_{d}}}=(0.43)(450N)=193.5N$
Por lo que la fuerza de fricción dinámica será de 193.5 N, con esto solucionamos el problema.
-
La fuerza de fricción no siempre se opone al movimiento, podrías explicar mejor el concepto porque queda corto.
-
Los felicito por la buena vocacion de ensenar
-
muy buena explicación
-
muy bueno!!
12 Deja tu comentario
Deja una respuesta

Estos temas te pueden interesar