Fuerza Magnética entre dos Conductores Paralelos
Ya que hemos hablado en el blog sobre los tipos de fuerzas magnéticas generada tanto por una partícula, así como la generada por un conductor, está también la fuerza magnética que es generada entre dos conductores paralelos por los que circula una corriente. ¿Pero cómo sucede dicho fenómeno? ¿qué debemos de tomar en cuenta?, veamos 😀
Sabemos que una carga en movimiento genera a su alrededor un campo magnético, cuando dos cargas se mueven en forma paralela interactúan sus respectivos campos y se produce una fuerza magnética entre ellas, y aquí tenemos dos consideraciones muy importantes.
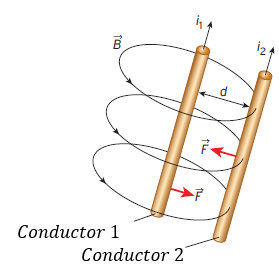
La fuerza magnética es de atracción si las cargas que se mueven paralelamente son del mismo signo y movimiento contrario.
La fuerza magnética es de repulsión si las cargas son de igual signo y con diferente sentido; o si son de signo contrario y su dirección es en el mismo sentido.
🧲 Fórmula de la Fuerza Magnética entre dos Conductores Paralelos
Entonces, cuando tenemos dos alambres rectos, largos y paralelos y por ellos circula una corriente eléctrica, debido a la interacción de los campos magnéticos esto producirá una fuerza entre ellos cuya magnitud está relacionada con la siguiente fórmula o expresión:
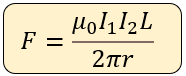
Dónde:
F = Magnitud de la fuerza magnética entre dos conductores rectos, largos y paralelos, se mide en Newtons (N)
µ0 = permeabilidad magnética del vacío
I1 = Intensidad de la corriente en el primer conductor (A)
I2 = Intensidad de la corriente en el segundo conductor (A)
L = longitud considerada de los conductores
r = Distancia entre los dos conductores, también sus unidades
Fórmula reducida del cálculo de la fuerza magnética
Existe una fórmula reducida para hacer más rápido los cálculo y esta fórmula nace de la relación que existe entre la permeabilidad del vacío y el 2π, es decir:
$\displaystyle \frac{{{{\mu }_{0}}}}{{2\pi }}$
asumiendo que π = 3.14 , podemos decir que:
$\displaystyle \frac{{{{\mu }_{0}}}}{{2\pi }}=\frac{{4\pi x{{{10}}^{{-7}}}}}{{2\pi }}=2x{{10}^{{-7}}}\frac{{Tm}}{A}$
a la parte de la potencia, la podemos simbolizar con una constante magnética, es decir:
$\displaystyle 2x{{10}^{{-7}}}=2{{K}_{m}}$
O sea que,
$\displaystyle {{K}_{m}}=1x{{10}^{{-7}}}$
Por lo que la fórmula reducida, la podemos apreciar de la siguiente manera:
📙 Ejercicios Resueltos de Fuerza Magnética entre dos Conductores Paralelos
Veamos algunos ejemplos para entender mucho mejor este tema:
Problema 1. Por un conductor recto circula una corriente de 10 A y a través de otro, que está paralelo a una distancia de 8 cm, circula una corriente de 5 A. Calcular la magnitud de la fuerza recibida por cualquiera de los conductores si su longitud es de 0.5 m y se encuentran en el aire. Además considere que si la corriente circula en diferente sentido por los conductores ¿la fuerza es de atración o repulsión?
Solución:
El problema es muy sencillo de resolver, basta con considerar los datos para poder sustituir en la fórmula, veamos:
Datos:
r = 8 cm = 0.08 m
I1 = 10 A
I2 = 5 A
L = 0.5 m
Ahora es momento de sustituir nuestros datos en la fórmula:
$\displaystyle F=\frac{{2{{K}_{m}}L{{I}_{1}}{{I}_{2}}}}{r}$
$\displaystyle F=\frac{{2\left( {1x{{{10}}^{{-7}}}} \right)\left( {0.5m} \right)\left( {10A} \right)\left( {5A} \right)}}{{0.08m}}=6.25x{{10}^{{-5}}}N$
que sería nuestro resultado.
6.25x10^-5 N
Al considerar que las corrientes van en diferente sentido, la fuerza es de repulsión.
Temas que podrían interesarte 👇