Fuerza Magnética sobre un Conductor Eléctrico
Una vez que hemos hablado sobre la fuerza magnética que actúa sobre una carga, es necesario explicar que esto no suele suceder solamente con cargas, sino también con otro tipo de objetos, en este caso en particular es sobre la fuerza magnética sobre un conductor por el que circula una corriente.
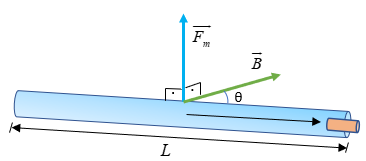
El conductor por el cual circula una corriente está rodeado de un campo magnético, si el conductor se introduce en forma perpendicular a un campo magnético recibirá una fuerza lateral cuya magnitud se puede apreciar en la imagen.
? Regla de la Mano Izquierda (Regla de Fleming)
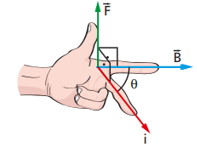
Para obtener el sentido de la fuerza, usamos la regla de la mano izquierda colocando el (dedo medio) en el sentido de la corriente, por lo cual la dirección de la fuerza será muy fácil de apreciar.
? Formula de la Fuerza Magnética sobre un Conductor por el que circula una Corriente
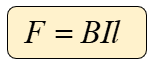
Dónde:
B = Inducción magnética, medida en teslas (T)
F = magnitud de la fuerza magnética que recibe el conductor, expresado en newtons (N)
I = intensidad de la corriente eléctrica que circula por el conductor medida en amperes.
l = longitud del conductor sumergido en el campo magnético
De la misma manera que sucede para una carga móvil, si el conductor por el cual circula una corriente forma un ángulo θ con el campo magnético, la fuerza recibida se determina con la siguiente expresión:
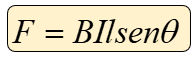
? Ejercicios Resueltos de Fuerza Magnética sobre un Conductor
Veamos algunos ejemplos de como resolver estos ejercicios de Fuerza Magnética sobre un conductor
Solución:
Este problema es importante porque nos ayudará a comprender la importancia del ángulo que se genera de acuerdo a la posición que posee el conductor, veamos la solución para cada inciso, teniendo en cuenta que primero debemos anotar nuestros datos:
Datos:
$\displaystyle I=5A$
$\displaystyle l=20cm=0.2m$
$\displaystyle B=4x{{10}^{{-3}}}T$
a)
Si el conductor es paralelo a las líneas de inducción magnética, el ángulo será de 0° , por lo que al aplicar la fórmula tendremos:
$\displaystyle F=BIlsen\theta =\left( {4x{{{10}}^{{-3}}}T} \right)\left( {5A} \right)\left( {0.2m} \right)sen0{}^\circ =0$
Como el seno de 0° = 0
la fuerza magnética es nula.
b)
Si el conductor se coloca de forma perpendicular a las líneas de inducción magnética, entonces tendremos un ángulo de 90°, por lo que al aplicar la fórmula, tendremos:
$\displaystyle F=BIlsen\theta =\left( {4x{{{10}}^{{-3}}}T} \right)\left( {5A} \right)\left( {0.2m} \right)sen90{}^\circ =4x{{10}^{{-3}}}N$
lo que resulta que la fuerza magnética sea de 4x10^-3 N
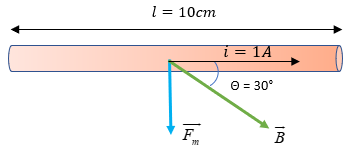
Solución:
Veamos los datos que tenemos:
Datos:
$\displaystyle I=1A$
$\displaystyle B=0.8T$
$\displaystyle l=10cm=0.1m$
$\displaystyle \theta =30{}^\circ $
La dirección y sentido de la fuerza magnética está dada por la regla de la mano izquierda o regla de Fleming. Si se observa en la imagen, podemos apreciarla mucho mejor. Aplicando la fórmula, obtenemos:
$\displaystyle F=BIlsen\theta =\left( {0.8T} \right)\left( {1A} \right)\left( {0.1m} \right)sen30{}^\circ =0.04N$
Por lo que la respuesta es F = 0.04 N
Deja una respuesta

Estos temas te pueden interesar