Fuerza Magnética Sobre Una Carga
Una vez comprendido el tema de campos magnéticos, es importante comprender también las fuerzas que actúan o están presentes, por eso la física es importante comprenderla para entender a que se deben estos fenómenos. Para empezar, se debe comprender que en todo conductor por el cual circula una corriente eléctrica está rodeado de un campo magnético. Y debemos comprender también que la corriente eléctrica es un flujo de electrones y cada partícula cargada en movimiento genera un campo magnético a su alrededor.
?Trayectoria de Cargas dentro de Campos Magnéticos
Cuando un electrón en movimiento con su propio campo magnético penetra en forma perpendicular dentro de otro campo producido por un imán o una corriente eléctrica, los dos campos magnéticos interactúan entre sí. Por lo que los campos magnéticos actúan sobre las partículas cargadas desviándolas de sus trayectorias a consecuencia del efecto de una fuerza magnética que lleva por nombre Fuerza de Ampere.
1️⃣ En la siguiente imagen podemos apreciar como una partícula cargada "q" describe una trayectoria circular como consecuencia de haber penetrado perpendicularmente a un campo magnético.

2️⃣ También tenemos el caso de que una partícula "q" que se mueve paralelamente a las líneas del campo magnético no sufra ninguna desviación.
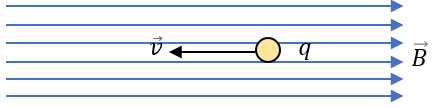
3️⃣ Y por último tenemos el caso que una partícula cargada "q" que penetra en forma oblicua a las líneas del campo magnético sea desviada y siga una trayectoria en espiral.

?? Fórmula de la Fuerza Magnética sobre una Carga
Una carga "q" cuyo movimiento es perpendicular a un campo magnético con una inducción magnética B a una cierta velocidad v, y además recibe una fuerza F se expresa matemáticamente de la siguiente manera:
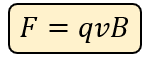
Dónde:
F = magnitud de la fuerza recibida por una partícula cargada en movimiento (N)
v = magnitud de la velocidad que lleva la carga (m/s)
B = Inducción magnética del campo, se mide en Teslas (T)
θ = ángulo formado por la dirección de la velocidad que lleva la partícula y la inducción magnética
q = carga en movimiento (C)
Cuando la trayectoria del movimiento de la partícula forma un ángulo con la inducción magnética B, entonces la fórmula se verá de la siguiente manera:
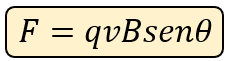
? Ejercicios Resueltos de Fuerza Magnética sobre una Carga
Ahora es momento de practicar 😀
Solución:
Para poder solucionar nuestro problema, es necesario colocar los datos que tenemos:
q = 1.6x10^-19 C
B = 0.45 T
v = 2x10^6 m/s
F = ?
Ahora procedemos a sustituir nuestros datos en la fórmula, para poder encontrar la magnitud de la fuerza.
$\displaystyle F=qvB$
$\displaystyle F=(1.6x{{10}^{{-19}}}C)(2x{{10}^{6}}\frac{m}{s})(0.45T)$
Multiplicamos, tanto la carga, como la velocidad, y el campo magnético
$\displaystyle F=1.44x{{10}^{{-13}}}N$
Por lo cual obtenemos:
Resultado:
$\displaystyle F=1.44x{{10}^{{-13}}}N$
Solución:
En este caso podemos observar que lo que nos pide el problema no es la fuerza magnética, pero si una de las variables que conforman a la fórmula, cual es el caso de la inducción magnética, así que anotamos los datos que tenemos:
q = 9uC
v = 3x10^5 m/s
F = 6x10^-3 N
B = ?
De la fórmula que ya conocemos
$\displaystyle F=qvB$
Vamos a despejar a "B" , si no te acuerdas como despejar, recuerda que puedes verlo aquí
$\displaystyle B=\frac{F}{{qv}}$
Sustituyendo nuestros datos en la fórmula:
$\displaystyle B=\frac{F}{{qv}}=\frac{{6x{{{10}}^{{-3}}}N}}{{\left( {9x{{{10}}^{{-6}}}C} \right)\left( {3x{{{10}}^{5}}\frac{m}{s}} \right)}}=\frac{{6x{{{10}}^{{-3}}}}}{{2.7}}=2.22x{{10}^{{-3}}}T$
Por lo que la inducción magnética es de:
Resultado:
$\displaystyle B=2.22x{{10}^{{-3}}}T$
-
1.- Un electrón en un tubo de rayos catódicos se mueve paralelo al eje del tubo a una velocidad de 10^7 m / s. Aplicando un campo de inducción magnética 2T, paralelo al eje del tubo, la fuerza magnética que actúa sobre el electrón es:
1 Deja tu comentario
Deja una respuesta

Estos temas te pueden interesar