Impulso Mecánico
Para entender el término de impulso mecánico, pensemos en una niña, que está sentada en un columpio y pide ser empujada, es necesario empujarla por un tiempo, para que adquiera la altura y velocidad que desea alcanzar. Los empujones se dan con un aumento gradual de la fuerza. Esto lleva implica algo de tiempo. Sin embargo, se podría alcanzar la misma altura en menos tiempo, siempre que la intensidad de la fuerza empleada sea mayor, es decir de empujón a empujón.
Y a esta acción se le conoce como impulso mecánico, una magnitud vectorial que representamos por I y se define como el producto de la fuerza por el intervalo de tiempo en el que esta actúa:
Sabemos que cuando una fuerza neta distinta de cero actúa sobre un cuerpo, lo pone en movimiento acelerado, variando su vector de velocidad. A esto añadimos ahora que tal cambio también depende de la duración de la aplicación de esta fuerza.
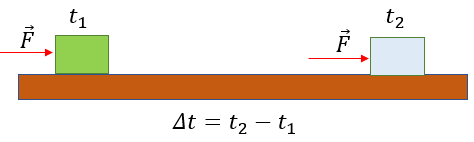
Hay otro punto importante: si la velocidad sufre una alteración, como resultado, la cantidad de movimiento del objeto también cambia; por lo tanto, existe una relación entre el impulso yla cantidad de movimiento, que veremos más adelante.
✅ Fórmula del Impulso Mecánico
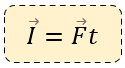
Dónde:
I = Impulso mecánico (N • s)
F = Fuerza aplicada en Newtons (N)
t = tiempo en que la fuerza actúa en segundos (s)
📏 Gráfica del Impulso Mecánico (F vs t)
La gráfica que relaciona el impulso mecánico es la siguiente, nótese de la Fuerza (eje vertical) y tiempo (eje horizontal)
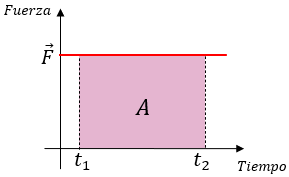
🏃♂️ Relación entre el Impulso y la Cantidad de Movimiento
A este relación también se le conoce como Teorema del Impulso, ahora bien como se puede observar, el impulso y la cantidad de movimiento están ligados en un solo concepto, ya que uno genera al otro. Todo parte desde la segunda Ley de Newton donde sabemos que la fórmula es la siguiente:
$\displaystyle F=ma$
y la magnitud de la aceleración de un cuerpo está dada por:
$\displaystyle a=\frac{{{{v}_{f}}-{{v}_{0}}}}{t}$
Sustituyendo en la 2da Ley de Newton:
$\displaystyle F=m\frac{{{{v}_{f}}-{{v}_{0}}}}{t}$
Al pasar "t" al otro miembro nos queda:
$\displaystyle Ft=m\left( {{{v}_{f}}-{{v}_{0}}} \right)$
Es decir:
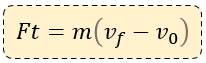
Esto nos dice que la magnitud del impulso (Ft) que recibe un cuerpo es igual al cambio en su cantidad de movimiento. Si el cuerpo parte del reposo (su velocidad inicial = 0 m/s), entonces:
$\displaystyle Ft=mv$
Es decir:
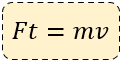
O dicho de otra forma:
$\displaystyle I=C$
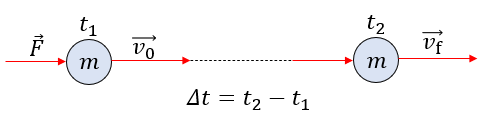
El impulso de una fuerza resultante F , que actúa sobre un cuerpo durante un intervalo de tiempo Δt, es igual a la variación de su cantidad de movimiento del cuerpo ocurrido en ese intervalo de tiempo.
📄 Ejercicios Resueltos de Impulso Mecánico
Ahora es momento de ejercitarnos un poco y realizar unos ejercicios.
Problema 1. ¿Qué impulso mecánico es transmitido a un carrito de juguete de 2 kg cuando una fuerza F constante de intensidad de 8 N es ejercida sobre el, durante 1.5 segundos conforme lo muestra la figura?
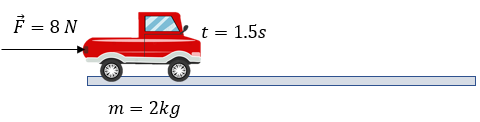
Solución:
Para darle solución a este ejercicio, nos debemos basar en los datos propuestos:
Datos:
F = 8 N
t = 1.5s
m = 2 kg
Aplicando la fórmula del impulso mecánico:
$\displaystyle I=Ft$
Sustituyendo datos:
$\displaystyle I=\left( {8N} \right)\left( {1.5s} \right)=12N\cdot s$
Que sería nuestro impulso:
I = 12 N · s
Problema 2. Un balón en reposo, cuya masa es de 0.45 kg es pateado por un jugador de fútbol, imprimiéndole una velocidad cuya magnitud es de 15 m/s. Si el tiempo que lo pateó fue de 0.03 s, ¿Cuál fue la magnitud de la fuerza ejercida sobre el balón?
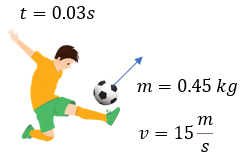
Solución:
Lo primero que haremos será colocar los datos y justamente de ahí partir a la solución:
Datos:
t = 0.03 s
m = 0.45 kg
v = 15 m/s
Para este caso aplicaremos la fórmula:
$\displaystyle Ft=mv$
puesto que la velocidad inicial del balón es en reposo.
Despejando a "F" de la fórmula:
$\displaystyle F=\frac{{mv}}{t}$
Sustituyendo nuestros datos en la fórmula:
$\displaystyle F=\frac{{mv}}{t}=\frac{{\left( {0.45kg} \right)\left( {15\frac{m}{s}} \right)}}{{0.03s}}=225N$
Obtenemos una fuerza ejercida sobre el balón de:
F = 225 N
Problema 3. Una pelota de 0.44 kg lleva una velocidad cuya magnitud es de 10 m/s y después es golpeada por un jugador, por lo que sale en la misma dirección pero en sentido contrario con una velocidad cuya magnitud es 12 m/s. La duración del golpe fue de 0.021 s. Calcular la magnitud de la fuerza ejercida sobre la pelota
Solución:
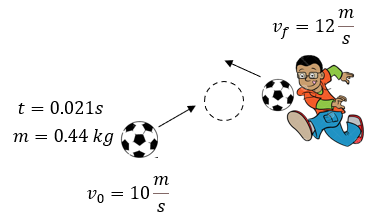
En este problema a diferencia del anterior, observemos que ahora si tenemos una velocidad inicial de la pelota, solo que cuando es golpeada por un jugador el balón toma un sentido diferente y velocidad distinta (la velocidad final), tomando en cuenta esta observación haremos lo siguiente en nuestros datos:
m = 0.44 kg
v0 = -10 m/s (el signo negativo indica que tenía sentido contrario al final del golpe)
vf = 12 m/s
t = 0.021 s
En este caso aplicaremos la siguiente fórmula:
$\displaystyle Ft=m\left( {{{v}_{f}}-{{v}_{0}}} \right)$
Despejando a "F"
$\displaystyle F=\frac{{m\left( {{{v}_{f}}-{{v}_{0}}} \right)}}{t}$
Sustituyendo nuestros datos en la fórmula:
$\displaystyle F=\frac{{m\left( {{{v}_{f}}-{{v}_{0}}} \right)}}{t}=\frac{{0.44kg\left[ {12\frac{m}{s}-\left( {-10\frac{m}{s}} \right)} \right]}}{{0.021s}}$
Después, obtenemos:
$\displaystyle F=\frac{{0.44kg\left( {22\frac{m}{s}} \right)}}{{0.021s}}=460.95N$
Qué vendría a ser la fuerza aplicada a la pelota:
F = 460.95 N
Temas que podrían interesarte 👇