Integrales por Fracciones Parciales
Aprende a resolver integrales por fracciones parciales con los cuatro casos distintos.
¿Quieres aprender a resolver integrales por el método de fracciones parciales?, pues seguimos con nuestros temas de cálculo integral. Hemos grabado varios videos para hacer más didáctico nuestro artículo, así que prepárate para aprender. En el cálculo integral, existen muchas técnicas para resolver integrales que no pueden solucionarse con reglas básicas como hemos visto en los métodos de integración anteriores. Una de ellas es la integració por fracciones parciales, que es especialmente útil cuando se quiere integrar una función racional, es decir, un cociente entre dos polinomios.
Este método se basa en descomponer una fracción compleja en varias fracciones más simples cuya integral si es conocida o más fácil de calcular. Esta técnica aunque no es precisamente del cálculo, sino del álgebra. Ya que se requiere que se sepa factorizar el denominador, y luego expresar la fracción original como suma de fracciones con denominadores más sencillos.
Identificar una integral por fracciones parciales
Esta es una de las dudas de mis alumnos a lo largo de mis 11 años enseñando cálculo, lo primero que debemos entender es que una fracción parcial tendrá la forma:
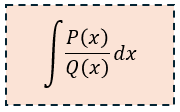
Dónde P(x) y Q(x) son polinomios, y el grado de P(x) es menor que el de Q(x) . Si el grado de P(x) es mayor o igual que el de Q(x) , primero se debe hacer una división polinómica para reescribir la expresión como un polinomio más una fracción propia.
Los Cuatro Casos de Fracciones Parciales
Esto es quizá lo más complicado de entender en los estudiantes, pero existen cuatro casos básicos del método de fracciones parciales, dependiendo el tipo de factores que aparecen en el denominador de la fracción racional.
Caso 1: Denominadores con factores lineales distintos
Si el denominador se puede factorizar como el producto de factores lineales diferentes, como:
$\displaystyle (x-a)(x-b)$
Entonces se descompone así:
$\displaystyle \frac{A}{{(x-a)}}+\frac{B}{{(x-b)}}$
Ejemplo:
Descomponer:
$\displaystyle \frac{{3x+5}}{{(x-2)(x+1)}}$
Forma:
$\displaystyle \frac{A}{{(x-2)}}+\frac{B}{{(x+1)}}$
Caso 2: Denominadores con factores lineales repetidos
Cuando el denominador tiene un factor lineal repetido, como:
$\displaystyle {{(x-a)}^{n}}$
Se descompone como una suma de fracciones con potencias crecientes:
$\displaystyle \frac{{{{A}_{1}}}}{{(x-a)}}+\frac{{{{A}_{2}}}}{{{{{(x-a)}}^{2}}}}+...+\frac{{{{A}_{n}}}}{{{{{(x-a)}}^{n}}}}$
Ejemplo:
Descomponer:
$\displaystyle \frac{{2x+1}}{{{{{(x-3)}}^{2}}}}$
Forma:
$\displaystyle \frac{A}{{(x-3)}}+\frac{B}{{{{{(x-3)}}^{2}}}}$
Caso 3: Denominadores con factores cuadráticos irreducibles
Si el denominador tiene un factor cuadrático que no se puede factorizar con números reales, o sea es irreducible, por ejemplo:
$\displaystyle {{x}^{2}}+bx+c$
Se usa la forma:
$\displaystyle \frac{{Ax+B}}{{({{x}^{2}}+bx+c)}}$
Ejemplo:
Descomponer:
$\displaystyle \frac{{{{x}^{2}}+1}}{{({{x}^{2}}+4)}}$
Forma:
$\displaystyle \frac{{Ax+B}}{{({{x}^{2}}+4)}}$
Caso 4: Factores cuadráticos irreducibles repetidos
Cuando un factor cuadrático irreducible está elevado a una potencia mayor a 1, como:
$\displaystyle {{(a{{x}^{2}}+bx+c)}^{n}}$
Se hace una suma anidada de fracciones con potencias crecientes:
$\displaystyle \frac{{\left( {{{A}_{1}}x+{{B}_{1}}} \right)}}{{\left( {{{x}^{2}}+bx+c} \right)}}+\frac{{\left( {{{A}_{2}}x+{{B}_{2}}} \right)}}{{{{{\left( {{{x}^{2}}+bx+c} \right)}}^{2}}}}+...+\frac{{\left( {{{A}_{n}}x+{{B}_{n}}} \right)}}{{{{{\left( {{{x}^{2}}+bx+c} \right)}}^{n}}}}$
Ejemplo:
Descomponer:
$\displaystyle \frac{{2x}}{{{{{\left( {{{x}^{2}}+1} \right)}}^{2}}}}$
Forma:
$\displaystyle \frac{{\left( {Ax+B} \right)}}{{\left( {{{x}^{2}}+1} \right)}}+\frac{{\left( {Cx+D} \right)}}{{{{{\left( {{{x}^{2}}+1} \right)}}^{2}}}}$
Integrales Resueltas por Fracciones Parciales
Llegó el momento de resolver ejercicios paso a paso, recuerda que existen videos que explican los problemas para evitar confundirte.
Solución:
Como el denominador es el producto de dos factores lineales distintos, usamos el caso de fracciones parciales con factores lineales simples:
$$\frac{5}{(x - 2)(x + 3)} = \frac{A}{x - 2} + \frac{B}{x + 3}$$
Multiplicamos ambos lados por \((x - 2)(x + 3)\):
$$5 = A(x + 3) + B(x - 2)$$
Expandimos:
$$5 = Ax + 3A + Bx - 2B = (A + B)x + (3A - 2B)$$
Igualamos coeficientes:
$$A + B = 0 \quad \text{y} \quad 3A - 2B = 5$$
Sustituimos \(B = -A\) en la segunda ecuación:
$$3A - 2(-A) = 5 \Rightarrow 3A + 2A = 5 \Rightarrow 5A = 5 \Rightarrow A = 1$$
Luego, \(B = -1\)
Sustituimos en la integral:
$$\int \frac{5}{(x - 2)(x + 3)}\,dx = \int \left( \frac{1}{x - 2} - \frac{1}{x + 3} \right)\,dx$$
Integramos término a término:
$$= \ln|x - 2| - \ln|x + 3| + C$$
Usamos propiedades de logaritmos:
$$= \ln\left| \frac{x - 2}{x + 3} \right| + C$$
Por lo tanto, la solución es:
$$\boxed{\int \frac{5}{(x - 2)(x + 3)}\,dx = \ln\left| \frac{x - 2}{x + 3} \right| + C}$$
¿Tuviste problemas para entender la integral?, no te preocupes mira el video paso a paso 👇
| 🎵 Ver en TikTok | 📷 Ver en Instagram |
Solución:
Factorizamos el denominador:
$$x^3 - x^2 - 2x = x(x^2 - x - 2) = x(x - 2)(x + 1)$$
Planteamos la descomposición en fracciones parciales:
$$\frac{4x - 2}{x(x - 2)(x + 1)} = \frac{A}{x} + \frac{B}{x - 2} + \frac{C}{x + 1}$$
Multiplicamos ambos lados por \(x(x - 2)(x + 1)\):
$$4x - 2 = A(x - 2)(x + 1) + B(x)(x + 1) + C(x)(x - 2)$$
Expandimos cada término:
\(A(x - 2)(x + 1) = A(x^2 - x - 2)\),
\(B(x)(x + 1) = B(x^2 + x)\),
\(C(x)(x - 2) = C(x^2 - 2x)\)
Sumamos los tres:
$$4x - 2 = A(x^2 - x - 2) + B(x^2 + x) + C(x^2 - 2x)$$
Agrupamos por potencias:
$$= (A + B + C)x^2 + (-A + B - 2C)x + (-2A)$$
Igualamos coeficientes:
1) \(A + B + C = 0\)
2) \(-A + B - 2C = 4\)
3) \(-2A = -2\)
De (3): \(A = 1\)
Sustituimos en (1): \(1 + B + C = 0 \Rightarrow B + C = -1\)
Sustituimos en (2): \(-1 + B - 2C = 4 \Rightarrow B - 2C = 5\)
Sistema:
- \(B + C = -1\)
- \(B - 2C = 5\)
Restamos:
\((B - 2C) - (B + C) = 5 - (-1) \Rightarrow -3C = 6 \Rightarrow C = -2\)
Sustituimos en \(B + C = -1\): \(B - 2 = -1 \Rightarrow B = 1\)
Entonces:
$$A = 1, \quad B = 1, \quad C = -2$$
Sustituimos en la integral:
$$\int \frac{4x - 2}{x(x - 2)(x + 1)}\,dx = \int \left( \frac{1}{x} + \frac{1}{x - 2} - \frac{2}{x + 1} \right)\,dx$$
Integramos término a término:
$$= \ln|x| + \ln|x - 2| - 2\ln|x + 1| + C$$
Agrupamos con propiedades logarítmicas:
$$= \ln\left| \frac{x(x - 2)}{(x + 1)^2} \right| + C$$
Por lo tanto, la solución final es:
$$\boxed{\int \frac{4x - 2}{x^3 - x^2 - 2x}\,dx = \ln\left| \frac{x(x - 2)}{(x + 1)^2} \right| + C}$$
¿Tuviste problemas para entender la integral?, no te preocupes mira el video paso a paso 👇
| 🎵 Ver en TikTok | 📷 Ver en Instagram |
Solución:
Primero factorizamos el denominador:
$$x^2 + 2x - 3 = (x + 3)(x - 1)$$
Ya que el denominador tiene dos factores lineales distintos, aplicamos el caso de fracciones parciales con factores simples:
$$\frac{4x + 5}{(x + 3)(x - 1)} = \frac{A}{x + 3} + \frac{B}{x - 1}$$
Multiplicamos ambos lados por \((x + 3)(x - 1)\):
$$4x + 5 = A(x - 1) + B(x + 3)$$
Expandimos:
$$4x + 5 = Ax - A + Bx + 3B = (A + B)x + (-A + 3B)$$
Igualamos coeficientes:
1) \(A + B = 4\)
2) \(-A + 3B = 5\)
Despejamos \(A = 4 - B\) y sustituimos en la segunda ecuación:
$$-(4 - B) + 3B = 5 \Rightarrow -4 + B + 3B = 5 \Rightarrow 4B = 9 \Rightarrow B = \frac{9}{4}$$
Entonces \(A = 4 - \frac{9}{4} = \frac{7}{4}\)
Sustituimos en la integral:
$$\int \frac{4x + 5}{(x + 3)(x - 1)}\,dx = \int \left( \frac{7}{4(x + 3)} + \frac{9}{4(x - 1)} \right)\,dx$$
Factorizamos constante:
$$= \frac{7}{4} \int \frac{1}{x + 3}\,dx + \frac{9}{4} \int \frac{1}{x - 1}\,dx$$
Integramos:
$$= \frac{7}{4} \ln|x + 3| + \frac{9}{4} \ln|x - 1| + C$$
También se puede escribir en forma logarítmica combinada:
$$= \ln\left| (x + 3)^{7/4} (x - 1)^{9/4} \right| + C$$
Por lo tanto, la solución final es:
$$\boxed{\int \frac{4x + 5}{x^2 + 2x - 3}\,dx = \frac{7}{4} \ln|x + 3| + \frac{9}{4} \ln|x - 1| + C}$$
¿Tuviste problemas para entender la integral?, no te preocupes mira el video paso a paso 👇
| 🎵 Ver en TikTok | 📷 Ver en Instagram |
Solución:
Como el denominador es \((x + 1)^2\), tenemos un **factor lineal repetido**, y usamos la forma:
$$\frac{x + 3}{(x + 1)^2} = \frac{A}{x + 1} + \frac{B}{(x + 1)^2}$$
Multiplicamos ambos lados por \((x + 1)^2\):
$$x + 3 = A(x + 1) + B$$
Expandimos:
$$x + 3 = Ax + A + B = Ax + (A + B)$$
Igualamos coeficientes:
1) \(A = 1\)
2) \(A + B = 3 \Rightarrow 1 + B = 3 \Rightarrow B = 2\)
Entonces:
$$\frac{x + 3}{(x + 1)^2} = \frac{1}{x + 1} + \frac{2}{(x + 1)^2}$$
Sustituimos en la integral:
$$\int \frac{x + 3}{(x + 1)^2}\,dx = \int \left( \frac{1}{x + 1} + \frac{2}{(x + 1)^2} \right)\,dx$$
Integramos término a término:
$$= \ln|x + 1| - \frac{2}{x + 1} + C$$
Por lo tanto, la solución final es:
$$\boxed{\int \frac{x + 3}{(x + 1)^2}\,dx = \ln|x + 1| - \frac{2}{x + 1} + C}$$
¿Tuviste problemas para entender la integral?, no te preocupes mira el video paso a paso 👇
| 🎵 Ver en TikTok | 📷 Ver en Instagram |
Solución:
Observamos que el denominador tiene un **factor lineal simple** \((x - 1)\) y un **factor lineal repetido** \((x + 1)^2\), por lo tanto usamos:
$$\frac{3x^2 + 5x}{(x - 1)(x + 1)^2} = \frac{A}{x - 1} + \frac{B}{x + 1} + \frac{C}{(x + 1)^2}$$
Multiplicamos ambos lados por \((x - 1)(x + 1)^2\):
$$3x^2 + 5x = A(x + 1)^2 + B(x - 1)(x + 1) + C(x - 1)$$
Expandimos cada término:
1) \(A(x + 1)^2 = A(x^2 + 2x + 1)\)
2) \(B(x - 1)(x + 1) = B(x^2 - 1)\)
3) \(C(x - 1)\)
Sumamos todo:
\[
3x^2 + 5x = A(x^2 + 2x + 1) + B(x^2 - 1) + C(x - 1)
\]\[
= Ax^2 + 2Ax + A + Bx^2 - B + Cx - C
\]\[
= (A + B)x^2 + (2A + C)x + (A - B - C)
\]
Igualamos coeficientes:
1) \(A + B = 3\)
2) \(2A + C = 5\)
3) \(A - B - C = 0\)
**Resolviendo el sistema:**
De (1): \(B = 3 - A\)
Sustituyamos en (3):
\(A - (3 - A) - C = 0 \Rightarrow A - 3 + A - C = 0 \Rightarrow 2A - C = 3\) (ec. 4)
Ahora usamos (2):
\(2A + C = 5\)
Sumamos (2) y (4):
\[
(2A + C) + (2A - C) = 5 + 3 \Rightarrow 4A = 8 \Rightarrow A = 2
\]
Sustituimos:
- \(B = 3 - A = 1\)
- De (2): \(2A + C = 5 \Rightarrow 4 + C = 5 \Rightarrow C = 1\)
Entonces:
$$\frac{3x^2 + 5x}{(x - 1)(x + 1)^2} = \frac{2}{x - 1} + \frac{1}{x + 1} + \frac{1}{(x + 1)^2}$$
Sustituimos en la integral:
\[
\int \frac{3x^2 + 5x}{(x - 1)(x + 1)^2}\,dx = \int \left( \frac{2}{x - 1} + \frac{1}{x + 1} + \frac{1}{(x + 1)^2} \right)\,dx
\]
Integramos término a término:
\[
= 2 \ln|x - 1| + \ln|x + 1| - \frac{1}{x + 1} + C
\]
Por lo tanto, la solución final es:
\[
\boxed{\int \frac{3x^2 + 5x}{(x - 1)(x + 1)^2}\,dx = 2 \ln|x - 1| + \ln|x + 1| - \frac{1}{x + 1} + C}
\]
¿Tuviste problemas para entender la integral?, no te preocupes mira el video paso a paso 👇
| 🎵 Ver en TikTok | 📷 Ver en Instagram |
Solución:
Primero factorizamos el denominador:
$$x^3 + 3x = x(x^2 + 3)$$
Entonces, la integral queda:
$$\int \frac{4x^2 + 6}{x(x^2 + 3)}\,dx$$
Ahora tenemos un **factor lineal simple** \(x\) y un **factor cuadrático irreducible** \(x^2 + 3\), por lo que la descomposición por fracciones parciales es:
$$\frac{4x^2 + 6}{x(x^2 + 3)} = \frac{A}{x} + \frac{Bx + C}{x^2 + 3}$$
Multiplicamos ambos lados por \(x(x^2 + 3)\):
$$4x^2 + 6 = A(x^2 + 3) + (Bx + C)(x)$$
Expandimos cada término:
- \(A(x^2 + 3) = Ax^2 + 3A\)
- \((Bx + C)(x) = Bx^2 + Cx\)
Sumamos:
\[
4x^2 + 6 = Ax^2 + 3A + Bx^2 + Cx = (A + B)x^2 + Cx + 3A
\]
Igualamos coeficientes:
1) \(A + B = 4\)
2) \(C = 0\)
3) \(3A = 6 \Rightarrow A = 2\)
Sustituimos:
- \(A = 2\)
- \(B = 4 - A = 2\)
- \(C = 0\)
Entonces:
$$\frac{4x^2 + 6}{x(x^2 + 3)} = \frac{2}{x} + \frac{2x}{x^2 + 3}$$
Sustituimos en la integral:
\[
\int \frac{4x^2 + 6}{x(x^2 + 3)}\,dx = \int \left( \frac{2}{x} + \frac{2x}{x^2 + 3} \right)\,dx
\]
Integramos término a término:
\[
= 2 \ln|x| + \int \frac{2x}{x^2 + 3}\,dx
\]
Para la segunda integral, usamos sustitución:
Sea \(u = x^2 + 3 \Rightarrow du = 2x\,dx\)
Entonces:
\[
\int \frac{2x}{x^2 + 3}\,dx = \ln|x^2 + 3|
\]
Por lo tanto, la integral completa es:
\[
2 \ln|x| + \ln|x^2 + 3| + C
\]
O bien, usando propiedades logarítmicas:
\[
\boxed{\int \frac{4x^2 + 6}{x(x^2 + 3)}\,dx = \ln\left(|x|^2 \cdot |x^2 + 3|\right) + C}
\]
Pero normalmente se presenta así:
\[
\boxed{\int \frac{4x^2 + 6}{x(x^2 + 3)}\,dx = 2 \ln|x| + \ln|x^2 + 3| + C}
\]
¿Tuviste problemas para entender la integral?, no te preocupes mira el video paso a paso 👇
| 🎵 Ver en TikTok | 📷 Ver en Instagram |
Ejercicios para practicar
1. $$\int \frac{3x + 4}{(x - 2)(x + 1)}\,dx$$
(Caso: Factores lineales simples)
2. $$\int \frac{x^2 + 5x + 2}{(x + 3)^2}\,dx$$
(Caso: Factor lineal repetido)
3. $$\int \frac{2x^2 + x + 7}{x(x^2 + 4)}\,dx$$
(Caso: Mezcla de factor lineal y cuadrático irreducible)
4. $$\int \frac{x^3 + 2x^2 + x + 1}{(x + 1)(x^2 + 1)}\,dx$$
(Caso: Grado del numerador mayor que el del denominador → requiere división previa)
5. $$\int \frac{5x^2 + 6x + 8}{(x^2 + 1)^2}\,dx$$
(Caso: Factor cuadrático irreducible repetido)
Deja una respuesta

Estos temas te pueden interesar