Ley de Boyle-Mariotte - Ejercicios Resueltos
Bien, bien! Hoy hablaremos sobre la ✅ ley de Boyle-Mariotte, y como siempre no me pondré hablar mucha la teoría porque entiendo que como estudiante lo que más detestamos es enrollarnos mucho con ello, y preferimos siempre la forma práctica. Es por ello que en este post, haré mención de como podemos enfrentarnos con esta famosa ley.
Antes que nada quiero decirte y hacerte entender que Boyle y Mariotte son dos científicos distintos, uno Irlandés y el otro Francés respectivamente, lo que quiero es que no vayas a pensar que esto se trate de una sola persona. Así que sabiendo esto, y con respeto a estos dos grandes científicos daremos inicio a el desglose del tema.
? Entendiendo la ley de Boyle Mariotte
El comportamiento de un gas va depender siempre de la relación que existan entre tres factores muy importantes, que son: el volumen, la presión y la temperatura. No obstante, estas relaciones fueron experimentadas por los científicos Boyle y Mariotte, de tal forma que dicho principio se generaliza como:
Si la temperatura permanece constante, el volumen de una masa gaseosa es inversamente proporcional a la presión que se le aplica.
Es muy probable que al leer el enunciado citado arriba, no lo entiendas del todo, y te doy la razón, está confuso en principio, pero aquí te diré que nos quiere dar a entender.
Vamos a establecer matemáticamente el enunciado.
$\displaystyle V\propto \frac{1}{P}$
Despejando, de tal forma que nos quede la unidad en el miembro derecho, tendremos algo así.
$\displaystyle PV\propto 1$
Introduciendo la constante de proporcionalidad, nos queda que:
$\displaystyle PV=K$
Ahora, si queremos ver los cambios que experimentará un gas, comúnmente se hace en un estado inicial y final, por lo que la expresión matemática o fórmula de Boyle-Mariotte queda de la siguiente forma.
$\displaystyle {{P}_{1}}{{V}_{1}}={{P}_{2}}{{V}_{2}}$
Dónde
$\displaystyle {{P}_{1}}=$ Presión inicial
$\displaystyle {{V}_{1}}=$ Volumen Inicial
$\displaystyle {{P}_{2}}=$ Presión Final
$\displaystyle {{V}_{2}}=$ Volumen Final
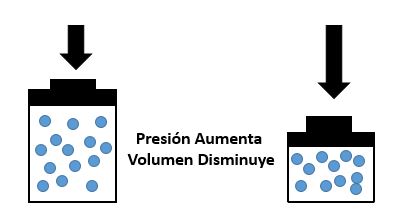
? Fórmula de la Ley de Boyle - Mariotte
En resumen, para la resolución de problemas de este tipo de ley, usaremos la fórmula:
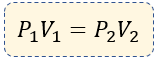
? Ejemplos resueltos de la ley de Boyle-Mariotte
Solución:
Lo primero que vamos analizar para la resolución del problema, son nuestros datos, saber que tenemos y que nos hace falta.
$\displaystyle {{V}_{1}}=$ 4.2 litros
$\displaystyle {{P}_{1}}=$ 760 mm de Hg.
$\displaystyle {{P}_{2}}=$ 415 mm de Hg.
$\displaystyle {{V}_{2}}=$ ?
Por lo que podemos observar el problema nos pide el volumen final es decir $latex \displaystyle {{P}_{2}}=$ , vamos a utilizar la fórmula de Boyle-Mariotte e iniciaremos a despejar la variable que necesitamos para poder iniciar a resolver el problema.
$\displaystyle {{P}_{1}}{{V}_{1}}={{P}_{2}}{{V}_{2}}$
Despejando >> $\displaystyle {{V}_{2}}$
$\displaystyle {{V}_{2}}=\frac{{{P}_{1}}{{V}_{1}}}{{{P}_{2}}}$
Sustituyendo nuestros datos.
$\displaystyle {{V}_{2}}=\frac{(760mmHg)(4.2l)}{415mmHg}=\frac{3192}{415}l=7.69l$
Por lo que nuestro volumen final es de $latex \displaystyle 7.69$ litros.
Con esto podemos concluir que mientras la presión bajó el volumen aumentó.
No es difícil analizar dichos problemas, veamos otro ejemplo.
Solución:
Al igual que el problema anterior lo que necesitamos es conocer nuestros datos, sin los datos no podemos hacer absolutamente nada, ahora hagamos de nuevo un listado de nuestros datos.
$\displaystyle {{V}_{1}}=$ 1.5 litros
$\displaystyle {{P}_{1}}=$ 2.5 atm.
$\displaystyle {{P}_{2}}=$ ?
$\displaystyle {{V}_{2}}=$ 3 l
Observamos que lo que nos falta es la presión final, por lo que vamos a despejar $latex \displaystyle {{P}_{2}}$ de la fórmula.
$\displaystyle {{P}_{1}}{{V}_{1}}={{P}_{2}}{{V}_{2}}$
Despejando >> $\displaystyle {{P}_{2}}$
$\displaystyle {{P}_{2}}=\frac{{{P}_{1}}{{V}_{1}}}{{{V}_{2}}}$
Sustituyendo nuestros datos.
$\displaystyle {{P}_{2}}=\frac{(2.5atm)(1.5l)}{3l}=\frac{3.75}{3}atm=1.25atm$
Tenemos que 1.25 atm. es la presión final de lo que nos pide nuestro problema, sin embargo el mismo problema dice que tenemos que convertir las unidades de presión, en este caso atmósferas a mm de Hg para ello haremos una regla de tres.
Si 1 atm equivale a 760 mm de Hg, 1.25 atm ¿a cuántos mm de Hg equivaldría?
1 atm ----------- 760 mm de Hg
1.25 atm ------------ x mm de Hg
$\displaystyle x=\frac{(760mmdeHg)(1.25atm)}{1atm}=950mmdeHg$
por lo que 950 mm de Hg es la presión final obtenida en un recipiente de 3 litros.
¿Aún no quedó claro?
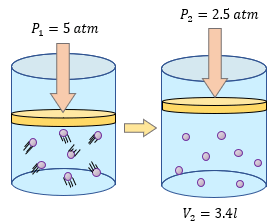
? Ejercicios para Practicar de la Ley de Boyle Mariotte
Para aprender mucho mejor el tema de la Ley de Boyle - Mariotte, es importante resolver más ejercicios y comprender los problemas para entender que variable tenemos que despejar y poder resolver sin ningún problema. Los siguientes ejercicios son explicados paso a paso en su solución, pero primero resuélvalos usted en su cuaderno o libreta. ??
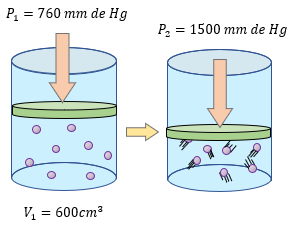
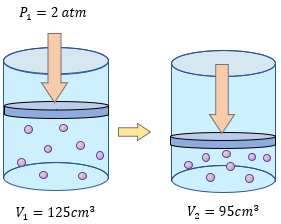
-
Muchas gracias me sirvio mucho
-
Hola una pregunta....? El volumen siempre sera en litros o en mililitros o si esta en mililitros se convierte a litros
-
Hola tengo una pregunta con la siguiente act:
-p1 : 1atm igual p2 : 2atm
-v1 : 3o L igual v2 : x -
Hola tengo me podrías orientar con el siguiente problema ...
Un gas que ocupa un volumen de 200 cm3 a una presión de 680 mmHg se deja expandir a una temperatura constante hasta alcanzar una presión de 0.35 atm ¿Cuál será su volúmen final en litros?
Gracias saludos! ☺️?
-
en un cilindro con tapa móvil de 5 cm2 de area de base, se halla un gas humedo a 7cenntigrado y hr =80%. calcular la fuerza que ejerce el gas seco sobre el area de la base. si la presion barometrica es de 766mmhg pvh2o(7centigrado) = 7,5mmhg Una ayuda por favor
-
Hola me puede ayudar con estos ejercicios 1 “una masa dada de gas en un recipiente recibe una presión absoluta de 7 atmósferas si temperatura es de 57•c y ocupa un volumen de 300 cm3 si el volumen del gas permanece constante y su temperatura aumenta 95•c cual será la presión absoluta del gas ? 2”calcular la temperatura absoluta a la cual se encuentra un gas que ocupa un volumen de 0.4 litros a una presión de una atmósfera si a una temperatura de 45•c ocupa un volumen de 1.2 litros a la misma presión 3”en un laboratorio hay una cantidad de 20 Mols de un gas perfecto que sufre expansión isotérmica la presión inicial de esta masa de gas es de 10 atm y el volumen de 8 L al final la expansión el volumen es de 40 L por lo tanto determina a) la presión final de la masa de gas b)la temperatura que se produce en la transformación le agradezco si me puede ayudar a resolverlos que no puedo
-
140 Deja tu comentario
Deja una respuesta

Estos temas te pueden interesar