Ley de Hooke - Ejercicios Resueltos
Después de un tiempo sin publicar algo relacionado a temas de física, vamos a comenzar con un tema muy importante dentro de las grandes aportaciones hechas por los físicos que dieron un cambio revolucionario a la física contemporánea. 😎
Hook trabajó fuertemente para entregar a la física un aporte que ha llevado a que hoy en día se fabriquen sistemas de suspensión para autos, juguetes de cuerda, relojes, entre otros.
Dicha investigación partía de un concepto donde un resorte era sometido a un peso sin que éste oscile, después el resorte experimentaría un estiramiento y al retirar el peso, el resorte volvería a su estado normal, a ese efecto se le denomina elasticidad.
⭐ La Ley de Hooke
El físico inglés en los años de 1968 y 1969 anunciaría esta ley como la ley de la proporcionalidad entre las deformaciones elásticas de un cuerpo y los esfuerzos a los que está sometido.
Matemáticamente se expresa mediante la siguiente forma:
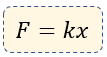
$\displaystyle F=k\cdot x$
Dónde:
$\displaystyle F$ = Fuerza que ejerce el resorte
$\displaystyle k$ = Constante de proporcionalidad
$\displaystyle x$ = Posición a la que se estira el resorte.
En la mayoría de los casos, la fórmula la encontraremos con un signo negativo, el signo negativo indica cuando el resorte se encuentra comprimido, y será positivo cuando el resorte esté estirado.
Sería interesante hablar más de este tema, sin embargo lo dejaremos para el tema del Módulo de Young.
Por ahora, veamos algunos ejercicios.
🔸 Ejemplos Resueltos de la Ley de Hooke
Problema 1.- Si a un resorte se le cuelga una masa de 200 gr y se deforma 15 cm, ¿cuál será el valor de su constante?
Solución:
Para poder resolver el problema, convirtamos las unidades dadas a unidades del Sistema Internacional, quedando así:
$\displaystyle m=200gr\left( \frac{1kg}{1000gr} \right)=0.20kg$
$\displaystyle x=15cm\left( \frac{1m}{100cm} \right)=0.15m$
$\displaystyle g=9.8\frac{m}{{{s}^{2}}}$
El problema nos proporciona una masa, pero hace falta una fuerza para poder realizar los cálculos, entonces multiplicamos la masa por la acción de la aceleración de la gravedad para obtener el peso, que finalmente es una fuerza.
$\displaystyle F=w=m\cdot g=\left( 0.20kg \right)\left( 9.8\frac{m}{{{s}^{2}}} \right)=1.96N$
Ahora solo queda despejar " k " en la fórmula de la Ley de Hooke.
$\displaystyle k=\frac{F}{x}$
Sustituyendo nuestros datos en la fórmula, tenemos:
🔹 Resultado:
$\displaystyle k=\frac{F}{x}=\frac{1.96N}{0.15m}=13.06\frac{N}{m}$
Veamos otro ejemplo:
Problema 2.- Una carga de 50 N unida a un resorte que cuelga verticalmente estira el resorte 5 cm. El resorte se coloca ahora horizontalmente sobre una mesa y se estira 11 cm. a) ¿Qué fuerza se requiere para estirar el resorte esta cantidad?
Solución:
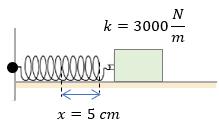
Primeramente se debe considerar que el problema nos implica dos etapas, en la primera debemos saber de que constante elástica se trata, para así en la segunda etapa resolver la fuerza necesaria cuando el resorte esté horizontalmente y finalmente poder graficar.
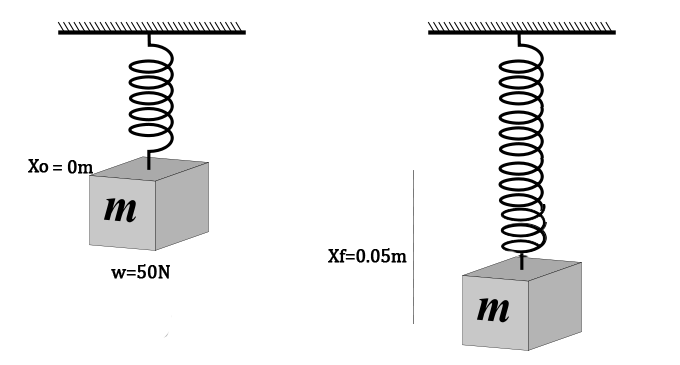
Necesitamos conocer el valor de " k " cuando nuestro sistema se encuentra de manera vertical, entonces despejamos y sustituimos nuestros datos:
$\displaystyle k=\frac{F}{x}=\frac{50N}{0.05m}=1000\frac{N}{m}$
Ahora pasamos a encontrar el valor de nuestra fuerza, esto ocurrirá cuando nuestro resorte esté de manera horizontal, entonces.
🔹 Resultado:
$\displaystyle F=kx=\left( 1000\frac{N}{m} \right)\left( 0.11m \right)=110N$
Esto quiere decir, que nuestro resorte necesita de 110 N, para poder estirarse 11 cm de su posición normal.
Veamos el último ejemplo:
Problema 3.- Se cuelga de un muelle una bola de masa de 15 kg, cuya constante elástica vale 2100 N/m, determinar el alargamiento del muelle en centímetros.
Solución:
Si tenemos la masa, podemos calcular el peso que finalmente viene siendo nuestra fuerza ejercida.
$\displaystyle w=m\cdot g=\left( 15kg \right)\left( 9.8\frac{m}{{{s}^{2}}} \right)=147N$
Ahora despejamos a " x " de la fórmula de la ley de hooke, quedando así:
$\displaystyle x=\frac{F}{k}=\frac{147N}{2100\frac{N}{m}}=0.07m$
Pero el problema, nos pide los valores en centímetros, por lo que realizamos nuestra conversión.
🔹 Resultado:
$\displaystyle x=0.07m\left( \frac{100cm}{1m} \right)=7cm$
Por lo que el alargamiento del muelle es de 7 centímetros.
Ejercicios resueltos, ¿tienes dudas? Hazlas en la caja de comentarios abajo, y si te gustó y te ayudó... 🙂
Por favor comparte, y ayúdanos a alfabetizar de manera científica a más personas 😎
📃 Ejercicios para Practicar de La Ley de Hooke
Para poder aprender mucho mejor este tema, te ponemos algunos ejercicios más para que puedas resolverlos en tu libreta y al final puedas comprobar tus resultados, recuerda dar click en "Ver Solución". 😊👇
Problema 4. Cuando una masa de 500 gr cuelga de un resorte, este se alarga 3 cm ¿cuál es la constante elástica?
Problema 5. La constante elástica de un resorte resultó ser de 3000 N/m ¿Qué fuerza se requiere para comprimir el resorte hasta una distancia de 5 cm?
-
-
Si tiene más información al respecto Jesús, háganos saberlo para poder colocarlo en el blog. Saludos
-
Mariana dice:
Hola me podrías ayudar
En este problema que no entiendo
Aun muelle se le aplica 10N de fuerza alcanzando una longacion de 4cm
¿Con varia la longitud de este resorte si se le aplica una fuerza de 15N?-
Isabel Cepeda dice:
Datos:
F= 10 N
∆x= 4 cm = 0.04 m
K= ?
Buscamos el valor de la constante:
K= F/∆x= 10 N/0.04 m= 250 N/m
Ahora determinamos la longitud del resorte al aplicarle la otra fuerza:
F= 15 N
K= 250 N/m Utilizamos la misma constante
∆x= ?∆x= F/k= 15N/250 N/m= 0.06 m = 6 cm
-
-
Edwin dice:
Hola me puedes ayudar con esta pregunta paso a paso por favor : Se requiere una fuerza de 28N para sostener un resorte qué está estirado desde su posición natural de 10cm a una longitud de 18cm. ¿Cuánto trabajo se necesitará para estirar el resorte de 18 a 25 cm?
-
-
Luciano sosa dice:
Tengo una pregunta, si el muelle tiene una constante de 800N y se le aplica una fuerza de 600N.¿Cuanto se comprimirá el muelle?
-
-
Tefy dice:
Ayuda por favor...
UNA FUERZA de 10 N se utiliza para comprimir un resorte con una constante de resorte dE 400N/m ¿Cuál es la comprensión del resorte.
Si se utilizaun trabajo de 3200j para estirar el mismo resorte, ¿Cuál es la longitud q se ha comprimido el resorte?-
-
Rubén dice:
Cuando una argolla de masa m=0,8kg
pasa por el punto B, el resorte de constante de rigidez cae kr=20 N y tiene su longitud natural. si la argolla parte del reposo del punto A y el radio del medio círculo r=0,06 m hallar la rapidez de la argolla en el punto C.-
Juan dice:
Ayuda por favor
-
-
-
-
-
¿Cómo?, debe haber algo que no entienda. Para poderle ayudar.
-
-
-
-
-
-
-
-
Gracias por los ejercicios, me sirvió mucho para estudiar con mi hija. En relación a las fechas, Robert Hook nació en 1635 y murió en 1703
Gracias otra vez-
Me da mucho gusto Pedro, y vamos a modificar esa fecha de Robert Hook. 😀
-
-
-
hola buen blog disculpa, ¿como se calcula la constante de rigidez de un resorte?
-
Hola Aurora, se necesita saber principalmente la frecuencia natural del elemento, para después analizarlo respecto a su peso y longitud, entre otras variables, pero es un tema más adelante de éste expuesto.
Saludos
-
Marhy dice:
Según la ley de Hooke.con respecto a la fuerza elástica cual es correcta.
Los elásticos y resortes no tienen relación con la fuerza elástica.La fuerza con la q tira el elástico,no tiene relación con la fuerza que volverá a su estado inicial
La fuerza con la que el elástico vuelva a su posición inicial no tiene relación con la fuerza con la que se le aplique al estirarlo.
La fuerza con la q el elástico vuelva a su posición inicial no tiene relación la fuerza que se le aplique al estirarlo.
-
-
Ana dice:
a un muelle que cuelga de un techo se le suspende una masa de 45 kg, y desplaza 38cm ¿cual es la constante de restitución de resorte?
-
-
-
ayuuuudaaaaaaaaaa.............. una varilla de acero de 20 metros de longitud tiene una trasversal de 0.30 cm2. Si en ella cuelga un objeto que tiene una masa de 550 kg. DETERMINA
el esfuerzo al que es sometida la varilla
la deformación de la varrilla si el modulo de young es de 20x10 a la 10 Pascales
el alargamiento de la varilla -
richard dice:
¿Como puedo aplicar esto a un ejercicio de un ascensor que se le revientan las cuerdas y baja en caida libre, y la recibe un resorte?
¿Cómo puedo calcular F en ese caso y como expresar la longitud acortada con la que queda el resorte, teniendo en cuenta que el ascensor cuenta con un sistema de seguridad de freno de fricción para reducir la velocidad de la caida libre y la amortiguación del impacto no sea tan fuerte?
ayuda, porfavor :'(-
menriquez dice:
por los pocos datos que proporcionas podria asumir lo siguiente:
w=mg seria el peso en vez de la fuerza que el resorte va a recibir como fuerza externa F=w(peso fuerza de friccion fr, fr-w= -kX fr - mg=-kX la longitud acortada seria calculado mediante X = -(fr-mg)/k como el peso es mayor que la fuerza de friccion quedaria del siguiente modo: X = (mg-fr)/k -
por los pocos datos que proporcionas podria asumir lo siguiente:
w=mg seria el peso en vez de la fuerza que el resorte va a recibir como fuerza externa F=w(peso) fuerza de friccion fr, fr-w= -kX fr - mg=-kX la longitud acortada seria calculado mediante X = -(fr-mg)/k como el peso es mayor que la fuerza de friccion quedaria del siguiente modo: X = (mg-fr)/k-
Marcela del pilar paez dice:
Se realiza una fuerza de 150N a un resorte que mide 0,25y se observa que el resorte se estiro alcanzando una longitud de 0,21m calcular el alargamiento del resorte y la constante elastica del resorte
-
-
VIcente Juan Montesinos Aguiló dice:
Seria un problema de energía acumulada. La energía acumulada en un resorte al comprimirlo es 1/2·K·x^2. Entonces la energía que lleva el ascensor al contactar con el muelle Ep=mgh será acumulada en el resorte hasta que se pare x(compresión del resorte) h altura de caída del ascensor. mgh=1/2·k·x^2.
-
-
yesi dice:
hola, he ... como decirlo estoy un poco confundida en un problema de física ¿me podrías ayudar un poquito?
-
maria dice:
9. Un resorte ligero con 500 N/m de constate de fuerza cuelga del techo con una masa de 2 Kg en su extremo inferior. La masa se suelta después de haber comprimido el resorte 0.15 m. Calcule la máxima distancia a la cual baja la masa respecto al punto donde el resorte está sin estirar ni comprimir.
🙁 -
-
David dice:
Hola, yo tengo una pregunta... ¿qué pasa si la fuerza de fricción influye en el problema, y quieres determinar el alargamiento de un muelle/resorte con un objeto de masa conocida colgando de el?
Gracias, saludos.-
Analiza bien el problema, si hay alguna fuerza adicional simplemente se le agrega, solamente considerando como actúa el fenómeno en el problema, bien puede sumarse o restarse.
Saludos.
-
Lux mariaj dice:
Si sobre un resorte colgamos una masa de 129 gramos, ¿Cuál es el valor de la fuerza externa aplicada?
-
-
Alina rodriguez dice:
Hola despues de hallar la K me piden que simule cada caso que quiere decir
-
-
francisco dice:
Muchas gracias, gracias a ti estoy aclarado con la ley de hook para mi examen de fisica
-
-
Samuel Guerra Garcia dice:
Si el peso de un cuerpo es de 1 kg estira un resorte de 2cm un resorte, ¿Cuanto se estirara el resorte al sostener una carga de 3 kg?
-
Martin dice:
Lo puedes hacer por regla de tres ya que la ley de hooke indica una proporcionalidad directa, es decir, si por cada kilo se estira 2cm en 3 kg se estiraria 2 x 3= 6cm
-
-
mabel dice:
como resolveria este ejercicio: un contrapeso de 64 lb está unido al extremo de un resorte y lo estira 0,32 pie, si patre de una posicion de 8 pulgadas sobre la posicion de equilibrio, con una velocidad de 5 pie/seg hacia abajo se pide.
a. Deducir la ecuacion de movimiento, la amplitud y el periodo.
b. ¿cuantas oscilaciones completas habra hecho el contrapeso a los 3 pi seg?
c.¿cual es la aceleracion a los 3 seg?-
-
Gabriela dice:
Hola buenas tardes me podría ayudar a resolver este problema aplicando la ley de Hooke.Si un peso de 10 Gr restira un resorte de 2cm¿Cuántos gramos se necesitan para estirar un resorte de 4,6,8,10 cm y Graficar?
-
-
-
-
heidy dice:
Muchísimas gracias es justo lo q yo necesitaba y gracias a tía primero dios tendré buena nota en la exposición gracias.
Saludos -
jesus dice:
hola necesito resolver el siguiente problema si un resorte k=13.06n.m sele cuelga una masa de 0.2000kg y se deforma 0.15 cual sera el valor de fuerza
-
Meylin dice:
Nesesito ayuda con un ejercicio....
Un resorte se alarga 6cm cuando se cuelga un bloque de 17 kg calcular la constante de elasticidad -
Para iniciar el tema los ejercicios son excelentes pero para ir avanzando se debe incrementar el grado de dificultad de los problemas, excelente explicación de los ejemplos.
-
Paula Ross dice:
Puede colgar ejemplos donde primero solo te den los datos de constante y elongación para solo calcular la fuerza? esto lo pasan a niños de 12 años. Los ejercicios son muy complejos para ppartir
-
Diego Agueros dice:
Me gusto mucho esta blog me sirvió para estudiar ya que tuve un examen muy importante el cual aprobé con un 7.5 muchas gracias Carlos y adiós
-
Paola dice:
Hola necesito hallar
La figura representa un resorte que se ha fijado al techo. Si la constante de
restitución de dicho resorte k= 1KN/m, y la masa de un 1000g se pone a
oscilar de manera que se mueve 0,02m desde su parte mas baja hasta la
mas alta.
a. Determinar lo que se estira el resorte cuando se le cuelga la masa
b. Escribir la ecuacion del sistema suponiendo que no hay fuerzas
disipativas y que el movimiento comenzo a observarse cuando la
masa se encontraba en reposo en la parte mas alta de la trayectoria.
c. Si se aumenta la masa al doble de su valor en que proporcion
cambiara el periodo de oscilacion del sistema.
Me podrías ayudar -
-
Arely Aidee Montoya Serralde dice:
Hola
necesito que me ayuden a resolver este ejercicioUn resorte cuya fuerza constante es de 12 lb / ft oscila hacia arriba y hacia abajo con un período de 0.56 segundos cuando una llave se suspende de él. ¿Cuánto pesa la llave?
-
Hola
Me podrian ayudar a resolver este ejercicio.Un resorte cuya fuerza constante es de 12 lb / ft oscila hacia arriba y hacia abajo con un período de 0.56 segundos cuando una llave se suspende de él. ¿Cuánto pesa la llave?
-
Elveen serrano dice:
Quiero que me ayuden con este problema,:se cuelga una masa de 4km se deforma 0.27M si a este resorte se le duplica la fueza de 20 N ¿cual es el valor y la distancia que se alarga el resorte al duplicarse la fuerza de 20 N
-
-
Agustín Franco dice:
Necesito ayuda con un problema.
Si tengo 2 resortes, “A" que su constante es de de 30kg/cm y “B" que es de 200g/cm.¿ Cuál de los dos resortes debo utilizar para pesar un cuerpo de 2 y 3 kg? -
Alex Gon dice:
Carlos Julian saludos me preguntaba por el segundo ejercicio ya que me confundi porque tenia entendido que para hallar x en ejercicios de elongación debo restar la longitud inicial a la longitud total para hallar X o sea que el resultado seria 0.06 y ese simple dato me altera todo el resultado. Ademas veo que multiplicaste K por la elongacion total y no por la X que deberia ser la resta de L1 a L te agradeceria que me aclararas esas dudas un fraternal saludo
-
dora montiel dice:
Si un resorte se le cuelga un peso de 500 g y se deformo 20cm. ¿Cuál será el valor de su constante?
-
Janna dice:
¿me podrían ayudar con este ejercicio?
Aplicaciones de las integrales en la Ciencia.
La ley de Hooke dice: La fuerza necesaria para estirar un resorte helicoidal es directamente proporcional al alargamiento. Un resorte tiene una longitud natural de 14 cm. Si una fuerza de 50 dinas se requiere para mantener el resorte estirado 2 cm
i. ¿Cuál es el valor de la constante k para este resorte?
ii. ¿Cuánto trabajo se realiza al estirar el resorte de su longitud natural hasta una longitud de 18 cm?
Gracias. -
G dice:
Ayudaaaa, no sé resolver este ejercicio, En la figura 3.81, p1= 141,42 Kp, P2= 40Kp. Si se supone que no hay rozamiento, calcular el alargamiento de los resortes sabiendo que la constante de elasticidad es 500Kp/m y el coeficiente de roce de 0,8
-
anyelly dice:
un resorte tiene una constante de elasticidad k= 13,06 N/m, si aplicar una fuerza este se deforma (alarga) 30 cm, cual es la magnitud de la fuerza...
-
diego dice:
Hola me podrían ayudar resolviendo un ejercicio.
Calcular la tensión unitaria o deformación lineal de un resorte de 0.25m cuando es comprimido por una fuerza que lo acorta a 0.2m -
ESTEFANIA dice:
me pueden ayudar por favor?:(
tengo un problema para resolver este ejercicio,no se que formula se ocupa:
¿Cuantos kilogramos tiene un cuerpo que pende de un resorte que se estira 4cm, si tiene una constante de 1100N/m? -
Andrea Albornoz dice:
Tenemos un soporte universal y un resorte colgando de el, en su extremo le colocamos un portapesas que tiene una flechita de indicador que apunta a una regla y contamos con seis pesas de 20 gramos. Si colocamos 60 gramos, que elongación alcanza el resorte?
-
Si el resorte alcanza una elongación de 75 mm, que peso tiene el portapesas?
Datos pesos en gramos0,20,40,60,80,100,120
Elongación del resorte en mm
45,75,105,135,165,195,225. -
alexandra dice:
2. Sobre un resorte se cuelga una masa de 250 g y produce una elongación de 50 cm. Contestar:
a. ¿De cuánto es la constante de recuperación elástica?
b. ¿Cuanta sería la elongación si fueran 100 g, 150 g, 200 g, 300 g, 500 g, y 1 Kg?
c. ¿Qué masa se debería colgar de un resorte para que logre una elongación de 10 cm? -
Luznairi Soto dice:
Por favor ¿me podrían ayudar con este ejercicio?
Un resorte cuya constante elástica es 302 N/m, está deformado 0,33 m. La energía potencial almacenada es -
spartan dice:
si quiero que me ayuden en esto: sobre un muelle de constante elastica 50 N/M y de longitud 20cm se ejerce una fuerza y el muelle se alarga hasta los 30cm ¿cual es el valor de la fuerza aplicada?
-
juan dice:
Hola, como se puede saber la constante elastica si es en forma horizontal? o solo se puede saber siendo de manera vertical?
-
VICENSSO CASSANO dice:
Si se tiene un resorte con una constante de elasticidad conocida, un cronómetro y un metro, ¿Cómo puede
determinarse el valor de una masa sujeta a ese resorte? -
Se realiza una fuerza de 150N a un resorte que mide 0,25y se observa que el resorte se estiro alcanzando una longitud de 0,21m calcular el alargamiento del resorte y la constante elastica del resorte
-
YOMAR MORALES F dice:
Hola me pueden ayudara resolver este ejercicio: La fuerza requerida para alargar un resorte que sigue la ley de Hooke varia a cero a 50.0 N cuando lo extendemos moviendo un extremo 12.0 cm desde su posición no deformada.
a) Encuentra la constante de fuerza del resorte
b) Determine el trabajo realizado en extender el resorte -
gregorio dice:
cual es la constante de elasticidad de un resorte si al ejercer sobre el una fuerza de 20 N se deforma 30 cm
-
Paco galo dice:
Cuando se le aplica a un muelle una fuerza de 100 se alarga 25cm.
¿Cual sera el valor de la constante elástica? -
Teresa dice:
Determinar la constante de un Resorte sí se coloca una Mada de 500gr la cual tiene una elongación de 33,5 in
-
Ana dice:
Sobre un resorte de 20 cm, se coloca una bola de acero de 1 kg que comprime al resorte 3 cm. Determina:
a) La constante de elasticidad del resorte. b) La fuerza que se debe aplicar sobre la bola para comprimir el resorte 2 cm más.
-
Angel R dice:
B.) A un objeto elàstico se le aplica una fuerza de 240 N y se deforma 120cm . Determina su constante de elasticidad.
-
Daniela dice:
Una cabina de ascensor pesa 3500 N y está sometida por un cable de 15 m compuesto por 7 alambres de acero cada uno de 3.2 mm de radio. Calcular ¿cuál es el alargamiento que experimenta cada alambre?
-
Gustavo Adolfo Ibañez dice:
Una carga de 15 N unida a un resorte que cuelga verticalmente estira el resorte 7 cm. El resorte se coloca ahora horizontalmente sobre una mesa y se estira 25 cm. a) ¿Qué fuerza se requiere para estirar el resorte esta cantidad?
-
Kelly dice:
Admitamos ahora que existe una fuerza de rozamiento, que produce un trabajo de 150 julios (que se convierte en calor) en todo el recorrido.
El resorte se comprime:
a. 0,125m
b. 0,25
c. 0,5m
d.1m
e. 2m -
christianm condor dice:
para colgar una maceta de flores de 6,2 kg, un jardinero usa dos cables: uno sujeto horizontalmente a una pared, el otro inclinado hacia arriba en un ángulo de θ = 40° y sujeto al techo. Encuentre la tensión en cada cable.
ayuda -
Eliza dice:
Hola, pueden ayudarme? De antemano gracias.
un resorte se estira 2.5 cm con 1.5 kg, que peso sera necesario para estirarlo 10 cm? -
Jessica dice:
Una pregunta si cada polea pesa 10N.Determinar el peso Q para que equilibre el conjunto.
-
Brithany Paredes dice:
Aquel que ayude en esto
Un resorte de 300 N/m se estira 200 cm cuando actúa una fuerza externa sobre él. Determine la magnitud de la fuerza.
-
un embolo de acero con 7.85 de densidad absoluta de 26 cm de diametro y 10 cm de altura, soporta un pequeño contrapeso; el cual encierra un gas y un resorte que se encuentra en equilibrio mecánico; el resorte se ha deformado 30cm(colocado verticalmente). si la presion barometrica es de 0.1 Mpa, la presion interna del gas es de 50Kpa. En el contacto del cilindro-embolo se produce una fuerza de friccion de 280N y la constante del resorte es de 5Kn/m.. si la aceleracion local de la gravedad es de 9.81 m/s cuadrado. Determinar la masa que debe tener el pequeño contrapeso.
-
Luz Mery Nova dice:
Porfavor me ayudas con este ejercicio qué no entiendo si un resorte se alarga 30cm aplicando una fuerza de 60N cuanto alarga si le aplicamos 120N
-
johis rivas dice:
cuando una masa de 300 kg cuelga de un resorte, este se alarga 10 cm. ¿Cuál es la constante elástica?
como hago hay quien me ayuda po favo
-
Sao00 dice:
La varilla delgada homogénea de masa despreciable y longitud l=0,2 m está
sujeta al piso por la bisagra sin fricción en el punto P. El resorte horizontal de constante e
lástica k=4,8 N/m enlaza el otro extremo de la varilla a una pared vertical. La varilla que
conduce una corriente de I=6,5 A está en un campo magnético uniforme de magnitud
B=0,34 T. (α=53º, m=10-3)
I) Hallar la deformación que experimenta la longitud del resorte, se estira E o comprime C
II) Hallar la energía almacenada en el resorte deformado, cuando la varilla está en equilibrio. -
noe dice:
Me podrias ayudar por favor es para una tarea de hoy
A un resorte de constante elástica 20 N/cm y de longitud natural 18 cm, se le aplica una fuerza de 80 N, entonces su longitud final será: -
Yamila dice:
Un resorte de 15 cm de longitud posee una constante elástica de 14
N/cm. Calcule la fuerza necesaria para estirarlo hasta una longitud de 28 cm. ¿Cuánto
se estirará si colgamos de él un objeto que pesa 50kg? -
Camila Acosta dice:
Me pueden ayudar en este problema
Un muelle se extiende 20 cm cuando se aplica una fuerza de 20N sobre el mismo.
A) calcular el valor de la constante elastica del muelle.
B) calcular la extension del muelle cuando se aplica una fuerza de 60N sobre el mismo. -
Miguel luna dice:
Sobre un resorte que tiene un coeficiente de elasticidad de 200 n/m actúa una fuerza de 100n cuanto se deforma el resorte y que energía potencial elástica se adquiere
-
miguel marambio dice:
Considera un amortiguador de un automóvil, el cual puede ser modelado como un resorte
con una constante de 2,14·105 N/m. Calcula la compresión que sufre dicho amortiguador con
respecto a su longitud natural, tomando en cuenta que el vehículo tiene una masa de 2 ton,
y a éste suben 2 personas de 70 kg cada una. La aceleración de gravedad (g) es 9,8 m/s2Se agradece.
-
rosa dice:
colgamos unas llaves de un muelle con k=2500n/m y comprobamos que la longitud del muelle es de 53 cm . ¿que fuerza peso ejercen las llaves? (dato:xo=0,40 m)
-
Josefa cid dice:
juan estira el resorte 0.8 metros ¿cual es la fuerza restauradora del resorte?
-
narcisa dice:
Calcule el alargamiento que sufre un muelle de constante elástica 135 N/m, cuando se aplica una fuerza de 65 N. Tener en consideración que el muelle presenta una longitud inicial de 105mm.
a.-Calcular la fuerza que se debe aplicar para que el muelle tenga un alargamiento de 27 cm.
C.- Un muelle se alarga 220mm cuando ejercemos sobre él una fuerza de 105Kp.
a.- Calcule el valor de la constante elástica del muelle.
b.- Calcule el alargamiento del muelle al aplicar una fuerza de 89N.
me puedes ayudar con este ejercisio muchas gracias -
victor dice:
me podrían ayudar con esto
Considera un amortiguador de un camión, el cual puede ser modelado como un resorte con
una constante de 2,14·106 N/m. Calcula la compresión que sufre dicho amortiguador con
respecto a su largo natural, tomando en cuenta que el camión pesa 100000 N y se carga con
2 ton de material. La aceleración de gravedad (g) es 9,8 m/s2
. -
Yeison Stiven dice:
Me puedes ayudar con este Si a un resorte se le cuelga una masa de 250 gr realizado una fuerza de 400 N y se deforma 0,15m ¿cuál será el valor de su constante?
-
Alexmy Karin Jiménez Hernández dice:
Hola me pueden ayudar con esta respuesta
A) al colgar un objeto de 25 libras de peso en un dinamómetro su resorte se estiraría 3cm. ¿Cuánto se estiraría el resorte si se colocara un objeto de 40 libras
-
Estefany dice:
Una carga de 350 N unida a un resorte que cuelga verticalmente estira el resorte 12 cm. El resorte se coloca ahora horizontalmente sobre una mesa y se estira 32 cm. a) ¿Qué fuerza se requiere para estirarel resorte esta cantidad? b) cual es su periodo de oscilación
-
Nombre dice:
Tengo una pregunta si un resorte experimenta un alargamiento de 7cm al soportar un peso en uno de sus extremos. Si un constante tiene un valor de 835n/m ¿Cuál es el valor de la fuerza de restauración?
-
-
Liceth Yuliana Roqueme Oviedo dice:
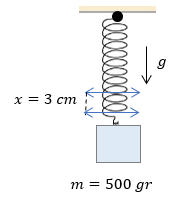
se cuelga una masa en un resorte que inicialmente mide 15cm y se observa que finalmente mide 25cm si la. constante de elasticidad del resorte es de 250n/m ¿ cuánto es el valor de la masa
144 Comentarios Publicados
benjamin 
yoarturo 
aa 
Sánchez 
irene 
Alex 
Sonia 
Antonio 
Juan 
jennifer 
Laura 
Samantha 
Juan 
Osiris 
Matias Bustos 
fred' 
FIDEL 
Marta 
Jazmin 
df 
Alejandra Vásquez 
Hugo 
Max 
Adam 
chupa pollas 
juan camilo 
ivan 
sofia vera 
Paola 
yolo man 
Victoria 
paquito el chocolatero 
ABIGAIL QUISHPE 
Isaac 
Alexandra 
Renato Tapia 
cami 
gadiel 
Alejandra Deja una respuesta
estan equivocadas las fechas 1968 y 1969