Ley de los gases ideales - Ejercicios Resueltos
Una vez comprendido los temas de las leyes de los gases, tales como la ley de Boyle - Mariotte, la Ley de Charles, la ley de Gay - Lussac, y finalmente la ley general del estado gaseoso. Es importante conocer también la ley de los gases ideales, porque son fundamentales para entender por completo la teoría general de los gases, un tema de gran relevancia en la termodinámica y estudios de química.
? ¿Qué es un gas ideal?
Para poder comprender completamente el tema del gas ideal o gas perfecto, debemos prestar atención a lo siguiente, un gas ideal o perfecto realmente no existe, es un gas hipotético cuyo compartimiento de las variables de presión, volumen y temperatura se pueden describir completamente por la ecuación del gas ideal. Dicha ecuación especifica la relación entre las cantidades de P, V, T y n.
Las moléculas que componen a un gas ideal no se suelen atraer o repeler entre si, y su volumen es despreciable en comparación con el volumen del recipiente que lo contiene. Aunque en nuestra naturaleza no exista el caso de un gas ideal, las diferencias entre el comportamiento de un gas real en márgenes de temperatura y presión no alteran sustancialmente los cálculos, por lo que podemos hacer uso de la ecuación con toda la seguridad, para resolver diversos ejercicios de gases.
? Constante Universal de los Gases
En nuestro estudio de las leyes de los gases, hemos visto la relación de la temperatura, presión y volumen. Tal como se muestra en la siguiente fórmula de la ley general de los gases:
$\displaystyle \frac{{{P}_{1}}{{V}_{1}}}{{{T}_{1}}}=\frac{{{P}_{2}}{{V}_{2}}}{{{T}_{2}}}$
Podríamos decir que la igualdad es igual a una constante en general, que la vamos a llamar "K".
$\displaystyle \frac{PV}{T}=K$
Si movemos a "T" para que pase a multiplicar a "K", la ecuación quedaría:
$\displaystyle PV=KT$
El valor de "K" lo vamos a relacionar en función del número de moles (n) de cualquier gas, esto tiene por ecuación la siguiente fórmula:
$\displaystyle K=nR$
Si sustituimos la K = nR en la ecuación que tenemos de Presión por Volumen, vamos a dar con la siguiente fórmula:
$\displaystyle PV=nRT$
Dónde:
P = Presión absoluta a la que se encuentra el gas
V = Volumen ocupado por el gas
n = Número de moles del gas que se calcula dividiendo su masa entre su peso molecular:
$\displaystyle n=\frac{m}{PM}$
R = Es la constante universal de los gases y su valor depende de las unidades usadas para su cálculo.
? Ecuación de la ley de los gases ideales
En conclusión, la fórmula que vamos a emplear para la ley de los gases ideales o gases perfectos es la siguiente:
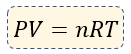
En algunos libros, hay autores que manejan esta fórmula como la Ecuación de Clapeyron
? ¿Cómo se obtiene R de la ley de los gases ideales?
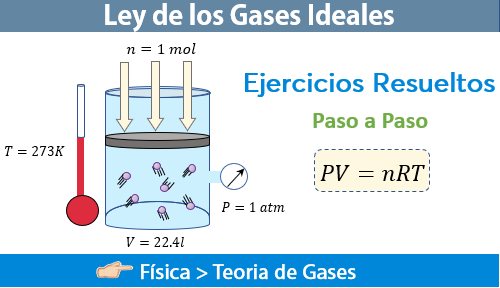
Para que podamos calcular el valor de R , tenemos que considerar que un mol de cualquier gas ideal y en condiciones normales de temperatura y presión, es decir a una atmósfera y 273 K, ocupa un volumen de 22.413 litros.
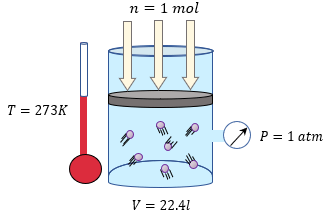
Por lo tanto, al despejar R de la ecuación anterior, tenemos:
$\displaystyle R=\frac{PV}{nT}=\frac{\left( 1atm \right)\left( 22.413l \right)}{\left( 1mol \right)\left( 273K \right)}=0.0821\frac{atm\cdot l}{mol\cdot K}$
Qué también es equivalente a:
R = 8.32 J/mol K
Para entender a fondo esta ley, veamos algunos ejercicios resueltos de la ley de los gases ideales o gases perfectos.
⭐ Ejercicios Resueltos de la Ley de los gases ideales
Vamos a comprender mejor el tema, con algunos ejercicios propuesto. Comencemos ??
Solución:
Si leemos el problema nuevamente, vemos que nos proporcionan datos como el volumen, la presión y la temperatura. Y nos pide calcular los moles de hidrógeno,es decir el valor de "n", después nos pide convertir esa cantidad de moles a unidades de masa, por lo que el problema es muy sencillo. Recordemos la fórmula:
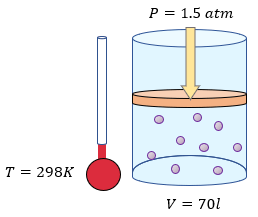
Datos:
$\displaystyle V=230l$
$\displaystyle P=1.5atm$
$\displaystyle T=35{}^\circ C+273=308K$
Nota: Observe que hemos convertido los grados celcius a la escala absoluta de Kelvin, sumando 273.
a) Obtener los número de moles de la masa de hidrógeno gaseoso
Veamos la ecuación de la ley de los gases ideales, de la fórmula:
$\displaystyle PV=nRT$
Despejamos a "n", y tenemos:
$\displaystyle n=\frac{PV}{RT}$
Ahora si podemos sustituir nuestros datos
$\displaystyle n=\frac{PV}{RT}=\frac{\left( 1.5atm \right)\left( 230l \right)}{\left( 0.0821\frac{atm\cdot l}{mol\cdot K} \right)\left( 308K \right)}=\frac{345atm\cdot l}{25.29\frac{atm\cdot l}{mol}}=13.64mol$
Por lo que la cantidad de número de moles es de 13.64 moles
b) Convertir en masa el número de moles
Al ser hidrógeno gaseoso nos referimos a que su peso atómico o masa molar es una molécula diatómica, compuesta por dos átomos de hidrógeno
$\displaystyle {{H}_{2}}$
Y que su peso molecular (PM) es igual a 2 g/mol (porque es diatómica), entonces tenemos:
$\displaystyle m=n\left( PM \right)=\left( 13.64mol \right)\left( 2\frac{g}{mol} \right)=27.28g$
Es decir que tenemos una masa de 27.28 gramos
Solución:
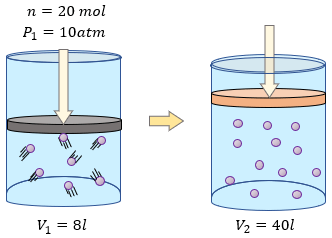
El problema es muy sencillo nuevamente de resolver, si volvemos a leer nos damos cuenta que tenemos los datos del número de moles de la sustancia, un volumen y una temperatura. También sabemos el valor de nuestra constante de gases ideales. Ahora es momento de colocar nuestros datos:
Datos:
$\displaystyle R=0.0821\frac{atm\cdot l}{mol\cdot K}$
$\displaystyle n=2.35mol$
$\displaystyle V=5.92l$
$\displaystyle T=71.5{}^\circ C+273=344.5K$
a) Obteniendo la presión ejercida por el gas
De nuestra ecuación de los gases ideales
$\displaystyle \begin{array}{l}PV=nRT\\m=n\left( PM \right)\end{array}$
Despejamos a la presión:
$\displaystyle P=\frac{nRT}{V}$
Sustituimos nuestros datos en la fórmula:
$\displaystyle P=\frac{nRT}{V}=\frac{\left( 2.35mol \right)\left( 0.0821\frac{atm\cdot l}{mol\cdot K} \right)\left( 344.5K \right)}{5.92l}=11.23atm$
Por lo que la presión es de 11.23 atmósferas
? Ejercicios para practicar de la ley de los gases ideales
-
Calcula el número de moles de aire (suponiendo que sus moléculas son todas iguales) que hay en una botella de agua vacía con capacidad de medio litro cuando se encuentra a nivel del mar (p=101300pa) y a temperatura ambiente (T=20°C)
-
Hola buenas tardes si me podrías ayudar
1. Calcular el número de moles ( suponiendo que todos sus moléculas son todos iguales ) que hay en una botella de agua vacía con capacidad de medio litro cuando se encuentra a nivel del mar (p=101300pa) y a temperatura ambiente (Y=20°c) -
Un gas ideal esta sometido a 2,8 atm, 200 ml y posee 0,25 moles ¿Cuál será su temperatura bajo esas condiciones?
-
Hola a mi me dio T:2.73 K
-
-
Un recipiente de 5,0 litros al que se ha hecho previamente el vacío, se llena de hidrógeno gaseoso. Si la temperatura es 27 °C y la presión 700 mm hg. A) cuántas moléculas de h2 contiene el matraz ?, B) cuál es la densidad del gas en estas condiciones ?
-
3.Un tanque que contiene gas natural mantiene su presión en 2.20 atm. En un día frio cuya temperatura es
de -15 °C, el volumen del gas en el tanque es de 28,5 pie³. El volumen que ocupará la misma cantidad de
gas en un día cuya temperatura es de 31°C es:
34 Deja tu comentario
Deja una respuesta

Estos temas te pueden interesar