Ley de Tangentes - Ejercicios Resueltos

Hey que tal!!! antes de iniciar el artículo, perdonar la falta de acentuación en el comic de arriba, pero el tipo de fuente no permite agregar acentos.. 🙁
Ahora si... En la semana publicamos dos artículos relacionados con la ley de senos y la ley de cosenos. En la cual se desarrollaron algunos ejercicios resueltos e indicado para que tipo de casos se suelen aplicar. Pero estoy seguro que también te has hecho la pregunta. ¿Y existirán también ley para las tangentes?
La respuesta es Siii! las tangentes también tienen sus propias leyes y sirven para lo mismo, para encontrar ya sea ángulos o lados de los triángulos oblicuángulos entonces ¿cómo podemos aplicarlo?
Fórmula para ley de tangentes
La fórmula para resolver ejercicios donde apliquemos ley de tangentes, es la siguiente:
$\displaystyle \frac{a-c}{a+c}=\frac{\tan \left( \frac{A-C}{2} \right)}{\tan \left( \frac{A+C}{2} \right)}$
$\displaystyle \frac{b-c}{b+c}=\frac{\tan \left( \frac{B-C}{2} \right)}{\tan \left( \frac{B+C}{2} \right)}$
$\displaystyle \frac{a-b}{a+b}=\frac{\tan \left( \frac{A-B}{2} \right)}{\tan \left( \frac{A+B}{2} \right)}$
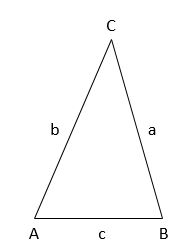
Puede ser un poco confuso entender teóricamente lo que significa, pero veamos un ejemplo resuelto.
Ejemplos resueltos de la ley de tangentes
Solución: Si observamos, tenemos el siguiente triángulo:
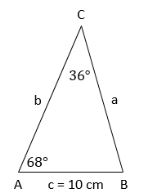
Si tenemos el lado c y el ángulo C podemos relacionarlo con otro lado y su ángulo opuesto, para esta ley no nos servirá de nada tener un lado que no conocemos y su ángulo opuesto que tampoco conocemos, necesitamos al menos un ángulo conocido y el lado opuesto o viceversa. 😎
En este ejemplo tenemos el ángulo A, pero nos falta su lado, entonces ahí si podemos aplicar nuestra ley de tangentes, para ello, usaremos la fórmula:
$\displaystyle \frac{a-c}{a+c}=\frac{\tan \left( \frac{A-C}{2} \right)}{\tan \left( \frac{A+C}{2} \right)}$
y sustituimos nuestros datos:
$\displaystyle \frac{a-10}{a+10}=\frac{\tan \left( \frac{68{}^\circ -36{}^\circ }{2} \right)}{\tan \left( \frac{68{}^\circ +36{}^\circ }{2} \right)}$
$\displaystyle \frac{a-10}{a+10}=\frac{\tan ({{16}^{{}^\circ }})}{\tan ({{52}^{{}^\circ }})}$
$\displaystyle \frac{a-10}{a+10}=\frac{0.2867}{1.2799}$
realizamos el cociente de los decimales de las tangentes.
$\displaystyle \frac{a-10}{a+10}=0.2240$
Empezamos a despejar nuestra variable "a"
$\displaystyle a-10=0.2240(a+10)$
$\displaystyle a-10=0.2240a+2.240$
$\displaystyle a-0.2240a=2.240+10$
$\displaystyle 0.776a=12.240$
$\displaystyle a=\frac{12.240}{0.776}=15.77cm$
$\displaystyle a=15.77cm$
que sería nuestro lado a, ahora podemos calcular nuestro lado restante, con la misma ley. Pero para ello, hay que conocer el ángulo B, que podemos hallarlo muy fácil mediante lo siguiente:
$\displaystyle \angle A+\angle B+\angle C=180{}^\circ $
$ \displaystyle 68{}^\circ +\angle B+36{}^\circ =180{}^\circ $
$\displaystyle \angle B=180{}^\circ -68{}^\circ -36{}^\circ $
$\displaystyle \angle B=76{}^\circ $
Por lo que tenemos el ángulo de B, ahora si podemos resolver mediante la ley, para encontrar el lado b
Podemos elegir el lado a y b, o podemos elegir la fórmula donde relaciona al lado c y b, eso queda a nuestra elección... Ya que podemos encontrar el lado de b, mediante las dos fórmulas:
$\displaystyle \frac{b-c}{b+c}=\frac{\tan \left( \frac{B-C}{2} \right)}{\tan \left( \frac{B+C}{2} \right)}$
$\displaystyle \frac{a-b}{a+b}=\frac{\tan \left( \frac{A-B}{2} \right)}{\tan \left( \frac{A+B}{2} \right)}$
En este caso, usaremos el lado a y b.
y empezamos a sustituir datos.
$\displaystyle \frac{15.77-b}{15.77+b}=\frac{\tan \left( \frac{68{}^\circ -76{}^\circ }{2} \right)}{\tan \left( \frac{68{}^\circ +76{}^\circ }{2} \right)}$
$\displaystyle \frac{15.77-b}{15.77+b}=\frac{\tan \left( -{{4}^{{}^\circ }} \right)}{\tan \left( {{72}^{{}^\circ }} \right)}$
$\displaystyle \frac{15.77-b}{15.77+b}=\frac{-0.0699}{3.0776}$
$\displaystyle \frac{15.77-b}{15.77+b}=-0.0227$
$ \displaystyle 15.77-b=-0.0227(15.77+b)$
despejando a "b"
$\displaystyle 15.77-b=-0.3579-0.0227b$
$\displaystyle -b+0.0227b=-0.3579-15.77$
$\displaystyle -0.9773b=-16.1279$
$\displaystyle b=\frac{-16.1279}{-0.9773}=16.5025cm$
$\displaystyle b=16.5025cm$
Y listo...! 😎
Con esta ley podemos encontrar también los lados y ángulos de un triángulo oblicuángulo...
Intenta bajar los ejercicios para la ley de senos, y resuélvelos por el mismo método 🙂
-
hola al iniciar a 68º le restas 36 y lo divides entre 2 da 16 por que pones 15? y cuando despejas la variable "a" pones un 0.776 o_O?
-
Hola! al despejar la variable "a" y no tener coeficiente, se considera que su coeficiente es 1. Este es el caso, por lo tanto sería 1a - 0,224 a.
Para resolver, agruparemos los términos semejantes restando sus coeficientes:
(1 - 0,224) a = 0,766 a
Y listo, Daniela!
-
-
hola perdona pero en donde se aplican las leyes de senos y ley de cosenos? POR FAVOR AIUDAAA DX
-
hola 🙂 quiero preguntar sobre los secantes de la trigonometria y me han ayudadon muchos tus ejerccios.
-
Hola, como resolvería un triángulo en el que me dan dos lados y un ángulo, con la ley de la tangente???
-
Hola 🙂
disculpa, cuando
comienzas a despejar "b", en el 3er paso ¿de donde sale -0.9773b? ayúdame por favor 😀-
holaaaaaaaaaaaaaaaaaa soy nuevo y soy maytematico con 15 años toy solito buco nv xD
-
28 Deja tu comentario
Deja una respuesta

Estos temas te pueden interesar