Leyes de Kepler - Ejercicios Resueltos

¡¡Buen día lectores!!, hace algún tiempo publicamos sobre el tema de la gravitación universal y resolvimos ejercicios que hicieron que comprendiéramos mucho mejor el tema de la atracción gravitatoria entre los planetas, pues bien hasta ahí todo bien. Pero para profundizar mejor el tema, tenemos que retroceder un poco al tiempo, es decir, mucho más antes de la aparición de las leyes de Newton, y nos remontemos al estudio de los planetas y sus movimientos, para conocer a fondo las Leyes de Kepler. Así que toma asiento, y prepárate para entender la breve historia y a resolver ejercicios. 👌

Empecemos hablando del astrónomo Johannes Kepler (1571-1630) , Kepler fue un grandioso y brillante astrónomo alemán, que aprendió de las enseñanzas tanto de Nicolás Copérnico como de Tycho Brahe, tanto que le causó demasiado interés en conocer como se movían los planetas alrededor del Sol, y que después de una tediosa investigación pudo confirmar que los plantes no se movían en forma circular, sino que se movían describiendo órbitas elípticas. Las cuales le permitió establecer varios enunciados matemáticos, relacionados con el sistema solar, y así poder formular tres leyes sobre el movimiento de los planetas, conocidos como las leyes de Kepler.

No obstante, miles de años atrás ya había mucho estudio referente al movimiento de los planetas y las estrellas. Por ejemplo en el siglo II d.C, el griego Claudio Ptolomeo había postulado la teoría de que la tierra era el centro del universo, esto paso a ser el famoso modelo geocéntrico, tiempo después a mediados del siglo XIV y comienzos del siglo XV el astrónomo Nicolás Copérnico fue capaz de demostrar que los planetas incluida la tierra en realidad se movían en órbitas circulares al rededor del Sol. Aunque ésto carecía de precisión tuvo que llegar el astrónomo danés Tycho Brahe donde perfeccionó las mediciones sobre el movimiento de los planetas. Pues para ese entonces el telescopio no se había descubierto.

Bien, pasemos a conocer las Leyes de Kepler.

Primera Ley de Kepler

La primera ley de Kepler o también llamada como la ley de órbitas, señala lo siguiente: Los planetas se mueven en órbitas elípticas, con el Sol en uno de los puntos focales. Veamos la siguiente imagen que describe el primer enunciado.

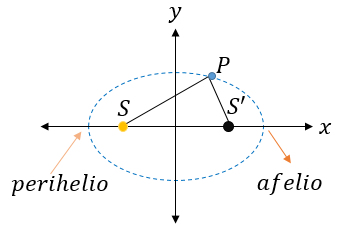
El punto de la órbita más cercano al Sol se le conoce como perihelio y el punto más lejano se le llama afelio, las elipses poseen una forma ovalada o de círculo aplanado, el ancho de ese círculo achatado se le conoce como "excentricidad", la parte que está sobre el eje "x" se le llama eje mayor, y del eje "y" se le conoce como eje menor.

Segunda Ley de Kepler

La segunda ley de Kepler o también llamada como la ley de áreas , es aquella ley que enuncia lo siguiente; Una linea del Sol a un planeta barre áreas iguales en lapsos de tiempo iguales. Veamos la imagen que lo describe mejor.

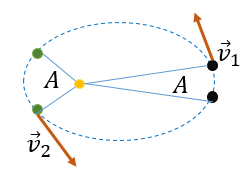
Esta ley nos indica que la rapidez orbital de un planeta varía en diferentes punto de su órbita. Debido a que la órbita del planeta es elíptica, su rapidez orbital es mayor cuando está más cerca del Sol que cuando está más lejos. Curiosamente Newton más tarde demostró que esto era consecuencia de su ley de la gravitación universal.

Tercera Ley de Kepler

La tercera ley de Kepler o también conocida como la ley de periodos , es una ley que establece que el cuadrado del periodo orbital de un planeta es directamente proporcional al cubo de la distancia promedio entre el planeta y el Sol; es decir que:

Es fácil deducir la fórmula de la tercera ley de Kepler, a partir de la ley gravitacional de Newton, e igualando con la fuerza centrípeta que proviene de la fuerza de gravedad. Teniendo en cuenta esto, entonces decimos que:

Fuerza Centrípeta = Fuerza Gravitacional

Entonces:

Dónde:

mp = Masa del Planeta

Ms = Masa del Sol

r = distancia

G = constante gravitacional

Despejando a la velocidad "v", tenemos que:

Pero como la velocidad es distancia sobre tiempo, y podemos interpretarla como la distancia del círculo (2πr) sobre el Periodo (tiempo que tarda en dar la vuelta).

Vamos a despejar al periodo "T"

Elevando al cuadrado ambos miembros, tenemos que:

Dejando fuera a r^3, tenemos que:

De aquí podemos tomar a lo siguiente como una constante, la constante de Kepler:

Podemos incluso, reescribir nuestra fórmula de la siguiente manera:

Ejercicios Resueltos de la Ley de Kepler

Para centrarnos en los ejercicios, tomaremos la fórmula de la tercera ley de Kepler que nos servirá para calcular ciertos datos, veamos entonces un ejemplo.

Ejemplo 1.- El planeta tierra posee un satélite natural llamado "Luna", Puesto que la luna se encuentra a una distancia promedio de 384,400 km de la tierra, y tiene un periodo orbital de 27 días, calcule la masa de la tierra.

Solución.

El problema nos proporciona algunos datos importantes como la distancia "r" y el valor del periodo "T", por lo que podemos calcular el valor de Kt, esto sería en unidades del Sistema Internacional, así que veamos:

Procedemos entonces al cálculo de K

De ahí tenemos que:

Entonces, podemos despejar de la fórmula de Kepler para la masa de la tierra:

De aquí despejamos a Mt

Entonces, la masa de la tierra es:

Vendría a ser un aproximado, pero sería la manera correcta de realizar el cálculo de la masa de la tierra.

Conclusión

Johanes Kepler fue un gran astrónomo, que con gran precisión trabajó la parte cinemática del sistema solar, aunque sin llegar a una explicación dinámica del mismo, es decir, cuáles fueron las causas que originan dichos movimientos. Sin embargo, la contribución a la astronomía es digna de elogio pues su investigación se llevó a cabo cuando aún no se había inventado el telescopio.