Leyes de Kirchhoff + Ejercicios Resueltos

Hoy tenemos un artículo muy esperado por muchos, y es que cuando nos adentramos en temas de electricidad y magnetismo, tenemos que pasar por temas muy interesantes e importantes en el análisis de circuitos, que como muchos sabrán, son las bases de diversas ingenierías, y tenemos que aprenderlas si o si, sin embargo si estás estudiando para aprobar tu examen de Física, también te servirá, así que presta atención 😀

Las leyes de Kirchhoff ⚡nos permiten resolver problemas de circuitos más complejos, no solamente recurriremos a la Ley del Ohm, sino que también tenemos que hacer un análisis más detallado en las redes básicas del circuito, así como los teoremas de voltajes y corrientes que iremos viendo más adelante.

Principios básicos de las Leyes de Kirchhoff

En algunos artículos anteriores calculamos resistencias en paralelo y en serie, también vimos resistencias mixtas y que en cualquier caso se basaban en la ley del ohm. En caso de no entender esta parte se sugiere repasar los siguientes posts y practicar los ejercicios resueltos.

• Resistencias en Serie - Ejercicios Resueltos [Paso a Paso]
• Resistencias en Paralelo - Ejercicios Resueltos [Paso a Paso]

Bien, en el caso de tener circuitos complejos como redes, mallas, puentes, estrella, o en forma de T, no podemos recurrir siempre en la Ley del Ohm, y tenemos que centrarnos en nuevas formas de resolver éste tipo de circuitos, es por ello que recurrimos a las Leyes de Kirchhoff 😎

Un Circuito de Corriente Continua o Directa (CD)

Para tener un ejemplo más claro sobre un circuito de mallas o nodos en corriente directa o continua, podemos ver la siguiente imagen:

Observamos la existencia de Nodos, Ramas, Mallas, también de fuente de voltaje, corrientes en las diversas ramas que llegan al nodo, así como resistencias.

⚠️ Observación:

Las resistencias se simbolizan de una forma diferente en los libros de Física e Ingeniería, lo cual es la manera correcta, pero con fines educativos y de agilizar nuestros diseños, hemos relacionado las resistencias en rectángulos naranjas. Pero no confundir.

Primera Ley de Kirchhoff – Ley de Corrientes (LCK)

La primera Ley de Kirchhoff también conocida como una de las Leyes de la conservación de la carga, nos advierte que "la suma algebraica de todas las corrientes que entran y salen de un nodo deben ser igual a cero".

Es decir:

$latex \displaystyle \sum{{{I}_{entran}}+\sum{{{I}_{salen}}=0}}$

Para entenderlo mejor, veamos la siguiente imagen:

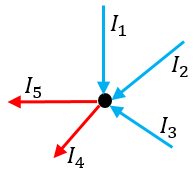
Aquí podemos observar claramente que las tres corrientes que ingresan al nodo son todas de valor positivo,  y las dos corrientes que salen del nodo, poseen un valor negativo. Eso significa que podemos reescribir la ecuación mediante la siguiente manera:

$latex \displaystyle {{I}_{1}}+{{I}_{2}}+{{I}_{3}}-{{I}_{4}}-{{I}_{5}}=0$

A menudo iremos usando un término llamado "Nodo", que seguramente ya lo has leído en el post, pues bien  un Nodo en un circuito eléctrico se refiere a una conexión o unión de dos o más rutas o elementos que conllevan corriente .

Veamos un ejemplo básico para entender la primera Ley.

Ejercicio Resuelto con el Método de Nodos o Ley de Corrientes

Solución:

Paso 1: Al analizar el circuito, debemos considerar que el único nodo de referencia es sin duda el nodo A, aunque muchos autores suelen nombrar los nodos con números u otras variables, nosotros le colocaremos la letra A, ahora debemos analizar que corrientes entran por ese nodo. Y vemos que:

$latex \displaystyle {{I}_{1}}+{{I}_{2}}={{I}_{3}}$

Entra la corriente 1, y corriente 2, y finalmente sale la corriente 3.

Paso 2: Como sabemos que la corriente es igual a la diferencia de potencial entre la resistencia (I = V/R) "Ley del Ohm", entonces podemos hacer nuestro siguiente análisis:

• La diferencia de potencial va desde la fuente hasta el nodo A, y entre ella solo se interpone la resistencia de 10Ω, por lo que nuestra corriente 1, es equivalente a:

$latex \displaystyle {{I}_{1}}=\frac{10v-{{V}_{A}}}{10\Omega }$

• Por otro lado la corriente 2, va desde la fuente hasta el nodo A, y entre ellas solo se interpone 20Ω, por lo que nuestra corriente 2, es equivalente a:

$latex \displaystyle {{I}_{2}}=\frac{20v-{{V}_{A}}}{20\Omega }$

• Finalmente la corriente 3, va desde el nodo A hasta el punto de abajo que consideraremos como tierra o referencia, por lo que lo único que interviene es una resistencia de 40Ω, quedando así:

$latex \displaystyle {{I}_{3}}=\frac{{{V}_{A}}}{40\Omega }$

Paso 3: Ahora es momento de unir la ecuación del paso 1, para formar una sola ecuación.

$latex \displaystyle \frac{10v-{{V}_{A}}}{10\Omega }+\frac{20v-{{V}_{A}}}{20\Omega }=\frac{{{V}_{A}}}{40\Omega }$

En la ecuación podemos encontrar el valor de voltaje en el nodo A, para ello solamente debemos multiplicar toda la ecuación por 40, para reducir los denominadores "mínimo común múltiplo".

$latex \displaystyle 40\left( \frac{10v-{{V}_{A}}}{10\Omega }+\frac{20v-{{V}_{A}}}{20\Omega } \right)=40\left( \frac{{{V}_{A}}}{40\Omega } \right)$

Simplificando.

$latex \displaystyle 4(10v-{{V}_{A}})+2(20v-{{V}_{A}})={{V}_{A}}$

Volvemos a multiplicar.

$latex \displaystyle 40v-4{{V}_{A}}+40v-2{{V}_{A}}={{V}_{A}}$

Ordenando las variables.

$latex \displaystyle -4{{V}_{A}}-2{{V}_{A}}-{{V}_{A}}=-40v-40v$

Sumando o restando respectivamente.

$latex \displaystyle -7{{V}_{A}}=-80v$

Despejando a nuestro Voltaje en el Nodo A

$latex \displaystyle {{V}_{A}}=\frac{-80v}{-7}\approx 11.43v$

Por lo que el Voltaje en A = 11.43 v

Paso 4: Como sabemos que la corriente 3, es la razón entre el voltaje en A y la resistencia de 40Ω, entonces proseguimos a calcular la corriente:

$latex \displaystyle {{I}_{3}}=\frac{{{V}_{A}}}{40\Omega }=\frac{11.43v}{40\Omega }=0.2858A$

Por lo que la corriente 3 es de 0.2858 Amperes.

Segunda Ley de Kirchhoff - Ley de Voltajes (LVK)

A diferencia de la primera ley, la segunda Ley de Kirchhoff es una clara idea sobre la Conservación de la Energía , que estable que "el voltaje total alrededor de un circuito es igual a la suma de todas las caídas de voltaje dentro del mismo ciclo", explicada de otra forma tendremos que recurrir a la siguiente imagen:

Sin importar en que punto del ciclo iniciemos y respetando la misma dirección obtendremos el resultado que explica la ley de voltajes, a menudo se irá usando el término "Malla" , el término malla se refiere  a un grupo de componentes como resistencias o fuentes, que están conectados entre dos nodos. 

📝 Nota:

Al igual que el ejemplo anterior de la ley de corrientes, podemos resolver el mismo ejercicio aplicando el método de mallas, o más bien de la ley de voltajes de Kirchhoff

Ejercicio Resuelto con el Método de Mallas o Ley de Voltajes

Solución: Al ser el mismo problema que en el ejemplo de nodos, en este caso tenemos que relacionar las caídas de voltajes en las resistencias, por lo que por ahora tenemos solamente 3 resistencias y 2 fuentes de voltaje. Recordar que tendremos que aplicar la Ley del Ohm donde sea necesario.

Paso 1: En nuestra primer malla tenemos una fuente de 10v y una corriente 1 que pasa por la resistencia R1, y también tenemos una resistencia R3 que pasan dos corrientes (1 y 2), esto nos da las pistas necesarias para elaborar nuestra primer ecuación:

$latex \displaystyle 10v={{I}_{1}}(10\Omega )+{{I}_{1}}(40\Omega )+{{I}_{2}}(40\Omega )$

Paso 2: Observemos que en este caso la malla 2, tenemos una fuente de 20v, también una resistencia R2 a la que le pasa una corriente 2, y posteriormente una resistencia R3 que le pasan dos corrientes (1 y 2), por lo que al elaborar nuestra ecuación tenemos:

$latex \displaystyle 20v={{I}_{1}}(40\Omega )+{{I}_{2}}(40\Omega )+{{I}_{2}}(20\Omega )$

Paso 3:  Empezamos a simplificar nuestras ecuaciones, para obtener una simultánea que iremos despejando.

$latex \displaystyle 10v={{I}_{1}}(10\Omega )+{{I}_{1}}(40\Omega )+{{I}_{2}}(40\Omega )$

$latex \displaystyle 20v={{I}_{1}}(40\Omega )+{{I}_{2}}(40\Omega )+{{I}_{2}}(20\Omega )$

Reduciendo

$latex \displaystyle 10v={{I}_{1}}(50\Omega )+{{I}_{2}}(40\Omega )$

$latex \displaystyle 20v={{I}_{1}}(40\Omega )+{{I}_{2}}(60\Omega )$

En este punto podemos aplicar cualquier método conocido para despejar a la corriente 1 o la corriente 2. Podemos aplicar el método de reducción:

• Método de Reducción

Aplicando el método de reducción, vamos a multiplicar la primera ecuación por 4 y la segunda ecuación por -5

$latex \displaystyle 4(10v)=4[{{I}_{1}}(50\Omega )+{{I}_{2}}(40\Omega )]$

$latex \displaystyle -5(20v)=-5[{{I}_{1}}(40\Omega )+{{I}_{2}}(60\Omega )]$

Una vez realizadas las multiplicaciones, entonces tenemos:

$latex \displaystyle 40v=200{{I}_{1}}+160{{I}_{2}}$

$latex \displaystyle -100v=-200{{I}_{1}}-300{{I}_{2}}$

Sumando ambas ecuaciones tenemos:

$latex \displaystyle -60v=-140{{I}_{2}}$

Invirtiendo la ecuación y despejando:

$latex \displaystyle {{I}_{2}}=\frac{-60}{-140}=0.4286$

Por lo que la Corriente I2 = 0.4286 Amperes

Ahora, calculando la corriente 1

Que la podemos despejar desde cualquiera de las dos ecuaciones, en este caso elegimos:

$latex \displaystyle 40v=200{{I}_{1}}+160{{I}_{2}}$

$latex \displaystyle 40v-160{{I}_{2}}=200{{I}_{1}}$

Despejando la corriente 1

$latex \displaystyle \frac{40v-160{{I}_{2}}}{200}={{I}_{1}}$

Invirtiendo la ecuación:

$latex \displaystyle {{I}_{1}}=\frac{40v-160{{I}_{2}}}{200}$

Asignando el valor de la corriente 2, que encontramos en los pasos más atrás.

$latex \displaystyle {{I}_{1}}=\frac{40v-160(0.4286)}{200}=\frac{-28.576}{200}=-0.1429$

Ahora para encontrar la corriente 3 que son la suma de la corriente 1 y 2, tenemos que aplicar:

$latex \displaystyle {{I}_{3}}=0.4286A+(-0.1429A)=0.2857A$

Lo que sería nuestra respuesta 😀

Conclusión

Al introducirnos a las leyes de Kirchhoff hemos aprendido lo que significa la primera ley de Kirchhoff que se conoce como ley de corrientes, y hemos aprendido sobre la segunda Ley de Kirchhoff que se refiere a la conservación de la energía, o más bien como la ley de voltajes, y hemos realizado el mismo ejercicio aplicando el método de nodos (1ra ley) y el método de mallas (2da ley), y el resultado ha sido el mismo.

¿Es complicado?, realmente no, solamente debemos tener cuidado con los signos y la forma de asignar nuestras corrientes. En otros artículos hablaremos a fondo de éstos métodos por separado y resolveremos más ejercicios propuestos paso a paso.