Momento Angular - Ejercicios Resueltos
Dentro de la dinámica rotacional nos encontramos con el tema de momento de inercia que explicamos con ejercicios resueltos, pero a su par también tenemos el tema de momento angular, el momento angular es una magnitud física fundamental que describe la rotación de un cuerpo alrededor de un punto fijo. Esta propiedad vectorial es crucial en la mecánica clásica y cuántica, representando la medida del movimiento rotacional de un sistema.
Por definición, la magnitud de la cantidad de movimiento angular, o simplemente magnitud del momento angular (L) de un cuerpo en rotación, es el producto de la magnitud de su momento de inercia (I) por la magnitud de su velocidad angular (ω) pero lo veremos más adelante para entender mucho mejor este concepto, por ahora quiero que tengas en cuenta esta definición para no confundirte y puedas captar el tema sin ningun problema, así como hemos explicado todos los temas de física en el blog.
Conservación de la cantidad de movimiento angular o del momento angular
Vamos a utilizar una imagen que usamos en el tema de momento de inercia para poder explicar incluso de donde obtenemos la fórmula del momento angular. Para ello veamos la siguiente imagen:
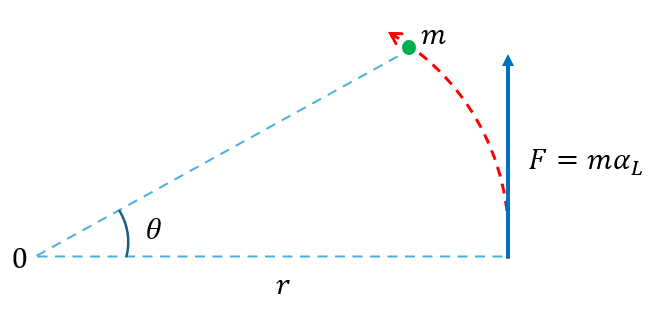
Cuando una partícula se encuentra girando (imagen de arriba) en determinado instante, la partícula tiene una velocidad lineal $\displaystyle {{\overrightarrow{v}}_{L}}$ y, por tanto, una cantida de movimiento lineal cuya magnitud se determina multiplicando su masa por la magnitud de su velocidad lineal $\displaystyle m{{v}_{L}}$
La magnitud del momento de su cantidad de movimiento lineal se define como $\displaystyle \left( {m{{v}_{L}}} \right)r$
Observen, como: $\displaystyle {{v}_{L}}=\omega r$ , siendo ω la velocidad angular de la partícula y r la distancia que hay de la partícula al eje de rotación, entonces tendremos:
$\displaystyle \left( {m{{v}_{L}}} \right)r=\left( {m\omega r} \right)r=\left( {m{{r}^{2}}} \right)\omega $
Pero sabemos que $\displaystyle I=m{{r}^{2}}$ (Fórmula del momento de inercia) , entonces obtenemos:
$\displaystyle L=I\omega $
Qué sería la fórmula que ocuperamos para el momento angular
Fórmula del Momento Angular
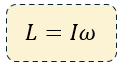
Las unidades de L en el Sistema Internacional son kg m²/s. Asi como la magnitud de la fuerza resultante es igual a la rapidez de cambio de la cantidad del movimiento lineal o momento lineal $\displaystyle \left( {F=\frac{{mv}}{t}} \right)$ , la magnitud del momento de rotación o magnitud del momento de una fuerza (τ) es igual a la rapidez de cambio de la cantidad de movimiento angular, o sea, igual a la rapidez de cambio del momento angular:
$\displaystyle \tau =\frac{{\Delta L}}{{\Delta t}}$
La ley de la conservación del momento angular señala que el momento angular total permanece constante, si no actúa sobre el sistema un momento de rotación externo no equilibrado.
Ejemplo en el Mundo Real sobre el Momento Angular
Un ejemplo práctico sobre la conservación del momento angular es el planeta tierra, ya que nuestro planeta durante millones de años ha girado con una magnitud de velocidad angular prácticamente constante. Cuando la inercia rotacional o momento de inercia (I) de un cuerpo en rotación cambia como consecuencia de una redistribución de su masa, debe cambiar su rapidez de rotación para que se conserve su momento angular.
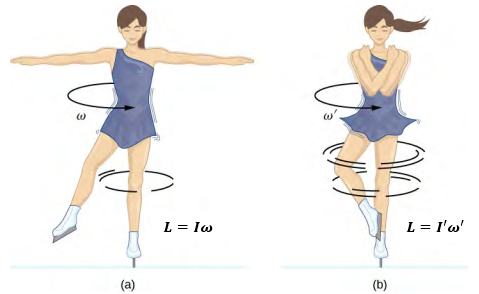
En la siguiente imagen vemos a una patinadora, observemos que en la imagen (a) la patinadora que está sobre hielo gira sobre la punta de su patín con los brazos extendidos. Su momento angular se conserva porque el torque neto sobre ella es despreciablemente pequeño. En la imagen (b) Su velocidad de giro aumenta considerablemente cuando retrae los brazos, lo que disminuye su momento de inercia. El trabajo que realiza para retraer los brazos da como resultado un aumento en la energía cinética rotacional.
Ejercicios Resueltos de Momento Angular
Problema 1. Una patinadora sobre hielo gira con los brazos extendidos a una velocidad angular de $\displaystyle {{\omega }_{0}}=3\frac{{rad}}{s}$ y su momento de inercia es de $\displaystyle {{I}_{0}}=4kg\cdot {{m}^{2}}$ . Luego, junta los brazos, disminuyendo su momento de inercia a $\displaystyle {{I}_{f}}=1kg\cdot {{m}^{2}}$ . ¿Cuál es su nueva velocidad angular?
Solución:
Se aplica la ley de la conservación del momento angular:
$\displaystyle {{L}_{{inicial}}}={{L}_{{final}}}$
$\displaystyle {{I}_{0}}{{\omega }_{0}}={{I}_{f}}{{\omega }_{f}}$
Sustituimos los valores en la fórmula:
$\displaystyle \left( {4kg{{m}^{2}}} \right)\left( {3\frac{{rad}}{s}} \right)=\left( {1kg{{m}^{2}}} \right){{\omega }_{f}}$
Resolviendo para $\displaystyle {{\omega }_{f}}$
$\displaystyle {{\omega }_{f}}=12\frac{{rad}}{s}$
Respuesta: Por lo tanto la nueva velocidad angular de la patinadora es de 12 rad/s
Problema 2. Un disco de masa $\displaystyle M=2kg$ y radio $\displaystyle R=0.5m$ gira con una velocidad angular inicial de $\displaystyle {{\omega }_{0}}=10\frac{{rad}}{s}$. Se deja caer una masa puntual de $\displaystyle m=0.1kg$ sobre el borde del disco. ¿Cuál es la nueva velocidad angular del sistema?
Solución:
Calculamos el momento de inercia del disco:
$\displaystyle {{I}_{{disco}}}=\frac{1}{2}MR^{2}=\frac{1}{2}\left( {2} \right)\left( {0.5} \right)^{2}=0.25kg\cdot {{m}^{2}}$
El momento de inercia de la masa puntual es:
$\displaystyle {{I}_{{masa}}}=mR^{2}=\left( {0.1} \right)\left( {0.5} \right)^{2}=0.025kg\cdot {{m}^{2}}$
Por conservación del momento angular:
$\displaystyle {{I}_{{total\omega 0}}}=\left( {{{I}_{{disco}}}+{{I}_{{masa}}}} \right){{\omega }_{f}}$
Sustituimos los valores:
$\displaystyle \left( {0.25} \right)\left( {10} \right)=\left( {0.25+0.025} \right){{\omega }_{f}}$
Resolviendo para $\displaystyle \omega f$:
$\displaystyle \omega f=9.09\frac{{rad}}{s}$
Respuesta: Por lo tanto, la nueva velocidad angular del sistema es de $\displaystyle 9.09\frac{{rad}}{s}$.
Problema 3. Un disco con $\displaystyle {{I}_{1}}=2kg\cdot {{m}^{2}}$ gira a $\displaystyle {{\omega }_{1}}=5\frac{{rad}}{s}$. Otro disco, inicialmente en reposo, con $\displaystyle {{I}_{2}}=1kg\cdot {{m}^{2}}$, cae sobre el primero. ¿Cuál es la velocidad angular final del sistema?
Solución:
Por conservación del momento angular:
$\displaystyle {{I}_{1}}{{\omega }_{1}}+{{I}_{2}}{{\omega }_{2}}=\left( {{{I}_{1}}+{{I}_{2}}} \right){{\omega }_{f}}$
Sustituimos los valores:
$\displaystyle \left( 2 \right)\left( 5 \right)+\left( 1 \right)\left( 0 \right)=\left( {2+1} \right){{\omega }_{f}}$
Resolviendo para $\displaystyle \omega f$ :
$\displaystyle \omega f=3.33\frac{{rad}}{s}$
Respuesta: Por lo tanto, la velocidad angular final del sistema es de $\displaystyle 3.33\frac{{rad}}{s}$.
Problema 4. Una partícula de masa $\displaystyle m=0.5kg$ se mueve en un círculo de radio $\displaystyle r=1m$ con velocidad lineal $\displaystyle v=4\frac{m}{s}$. ¿Cuál es el momento angular de la partícula con respecto al centro del círculo?
Solución:
El momento angular se calcula como:
$\displaystyle L=mvr$
Sustituimos los valores:
$\displaystyle L=\left( {0.5} \right)\left( {4} \right)\left( {1} \right)=2kg\cdot {{m}^{2}}/s$
Respuesta: Por lo tanto, el momento angular de la partícula es de $\displaystyle 2kg\cdot {{m}^{2}}/s$.
Problema 5. Un trompo gira con una velocidad angular inicial de $\displaystyle {{\omega }_{0}}=20\frac{{rad}}{s}$. Su momento de inercia es $\displaystyle I=0.1kg\cdot {{m}^{2}}$. Si un freno genera un torque constante de $\displaystyle \tau =-0.02N\cdot m$, ¿cuánto tiempo tardará el trompo en detenerse?
Solución:
La relación entre torque y aceleración angular es:
$\displaystyle \tau =I\alpha$
Resolviendo para $\displaystyle \alpha$:
$\displaystyle \alpha =\frac{\tau }{I}=\frac{-0.02}{0.1}=-0.2\frac{{rad}}{{s}^{2}}$
Usamos la ecuación del movimiento angular:
$\displaystyle \omega ={{\omega }_{0}}+\alpha t$
Como el trompo se detiene, $\displaystyle \omega =0$:
$\displaystyle 0=20+\left( -0.2 \right)t$
Resolviendo para $\displaystyle t$:
$\displaystyle t=\frac{20}{0.2}=100s$
Respuesta: Por lo tanto, el trompo tardará $\displaystyle 100s$ en detenerse.
Deja una respuesta
Temas que podrían interesarte 👇