Momento de Inercia - Ejercicios Resueltos

Una de las cosas más importantes dentro de la Física, sin duda es el momento de inercia o de inercia rotacional. Este tema en general nos da razón del porque cuando un cuerpo gira, trata de continuar así y uno sin girar trata de continuar sin hacerlo, así como también de explicar la propiedad de los cuerpos de oponerse a cambios en su estado de movimiento de rotación. El momento de inercia está representada por la letra $\displaystyle I$

Además también veremos ejercicios resueltos paso a paso, tomando en cuenta el momento de inercia de ciertas figuras regulares que serán de gran ayuda para el cálculo de estos problemas.

¿De qué depende el Momento de Inercia o Inercia Rotacional?

El momento de rotación o momento de fuerza (τ) no equilibrado y que actúa sobre un cuerpo, produce una cierta magnitud de aceleración angular (α) que se expresa por la siguiente ecuación:

$\displaystyle \tau =I\alpha $

Como ya se dijo, I representa la magnitud del momento de inercia rotacional en torno al eje de rotación.

Sabemos que un cuerpo rígido está formado por una multitud o cúmulo de partículas, si nosotros aplicamos la segunda Ley de Newton a una sola partícula que gira. Considerando la magnitud de una fuerza resultante F que actúa sobre una partícula de masa (m) en una dirección perpendicular al radio (r) de una circunferencia, como se aprecia en la imagen.

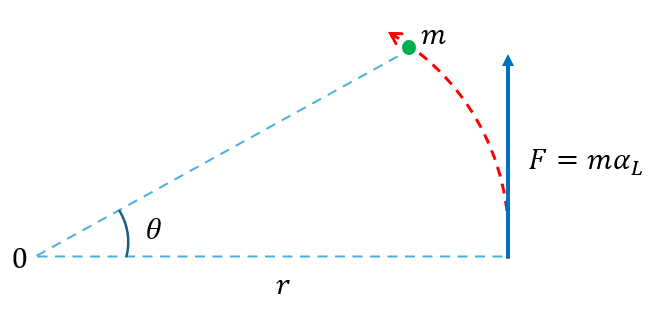
La magnitud de la fuerza que produce una aceleración lineal $\displaystyle {{\alpha }_{L}}$ es igual a:

$\displaystyle F=m{{\alpha }_{L}}$

Si multiplicamos por r cada miembro de la igualdad, tendremos lo siguiente:

$\displaystyle Fr=mr{{\alpha }_{L}}$

Sabemos que en la aceleración angular se expresa por:

$\displaystyle \alpha =\frac{{{{\alpha }_{L}}}}{r}$

De dónde: $\displaystyle {{\alpha }_{L}}=\alpha r$

Entonces lo escribimos:

$\displaystyle Fr=Mr\alpha r=m{{r}^{2}}\alpha $

El producto Fr representa la magnitud del momento de rotación o momento de una fuerza (τ) que produce una aceleración angular (α). El producto mr² corresponde a la magnitud del momento de inercia rotacional (I) de la partícula en torno al eje que pasa por el punto 0, de tal manera que:

$\displaystyle \tau =m{{r}^{2}}\alpha $

es decir:

$\displaystyle \tau =I\alpha $

Las unidades de I en el Sistema Internacional son kg m²

Momento de Inercia en Cuerpos Extensos

Cuando hablamos del momento de inercia de un cuerpo, estamos midiendo cómo está distribuida su masa respecto al eje de rotación y cómo eso afecta su resistencia a cambiar su movimiento de rotación. Si el cuerpo es pequeño o está compuesto por una sola masa puntual, podemos usar la fórmula básica $\displaystyle I=m{{r}^{2}}$ , donde m es la masa y r es la distancia de esa masa al eje de rotación.

Sin embargo, cuando un cuerpo tiene un tamaño considerable y no es solo un punto, está formado por muchas partículas con diferentes masas distribuidas a diferentes distancias del eje de rotación. En este caso, el momento de inercia no se puede calcular con una fórmula tan simple, porque debemos considerar cada una de esas partículas de forma individual.

Veamos la imagen de abajo: Dos partículas de masa m1 y m2 se ubican en cada extremo de una varilla de masa despreciable que puede girar alrededor de un eje que pasa por el centro de gravedad del sistema y que es perpendicular a la línea que une las partículas. La magnitud del momento de inercia total del sistema en toro al eje estará dado por: $\displaystyle I={{m}_{1}}{{r}_{1}}^{2}+{{m}_{2}}{{r}_{2}}^{2}$

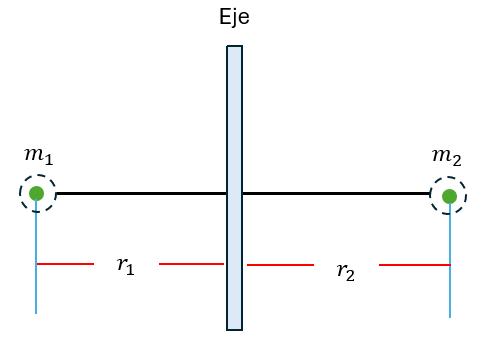
Pero, para un cuerpo cuyo tamaño sea considerable, se puede establecer una expresión similar al de la imagen de arriba, pero contendría muchos términos, por ejemplo para hacerlo, usamos una fórmula extendida:

$\displaystyle I={{m}_{1}}{{r}_{1}}^{2}+{{m}_{2}}{{r}_{2}}^{2}+{{m}_{3}}{{r}_{3}}^{2}+...+{{m}_{n}}{{r}_{n}}^{2}$

Dónde:

$\displaystyle {{m}_{1}},{{m}_{2}},{{m}_{3}},...{{m}_{n}}$ son las masas de las partículas que forman el cuerpo.

$\displaystyle {{r}_{1}},{{r}_{2}},{{r}_{3}},...{{r}_{n}}$ son las distancias de cada una de esas partículas al eje de rotación.

Esto significa que el momento de inercia total de un cuerpo es la suma de los momentos de inercia de todas sus partículas individuales. Cada término de la suma representa el aporte de una de esas partículas, dependiendo tanto de su masa como de qué tan lejos está del eje.

En resumen, calcular el momento de inercia de un cuerpo grande implica considerar cada parte del cuerpo como si fuera una pequeña masa puntual y sumar las contribuciones de todas esas masas. Es por eso que el momento de inercia varía dependiendo no solo de la cantidad de masa, sino también de cómo está distribuida esa masa alrededor del eje de rotación.

Momentos de Inercia de Cuerpos Rígidos de Forma Regular

Por ejemplo para algunos cuerpos de alta simetría, se calculan fácilmente en cualquier caso en que el eje de rotación se localice en un eje de simetría. Veamos algunos ejemplos:

Momento de Inercia de un anillo cilíndrico

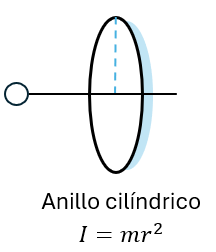
Momento de inercia de un cilindro hueco de paredes delgadas

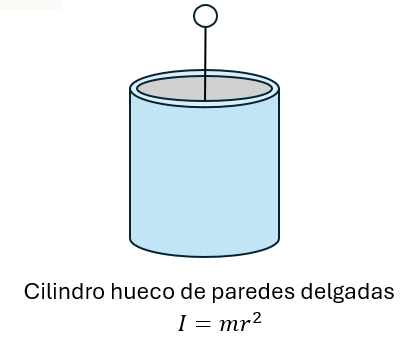
Momento de inercia de una esfera sólida

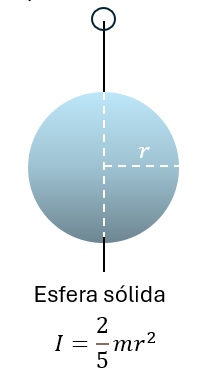
Momento de inercia de una varilla delgada de longitud "l"

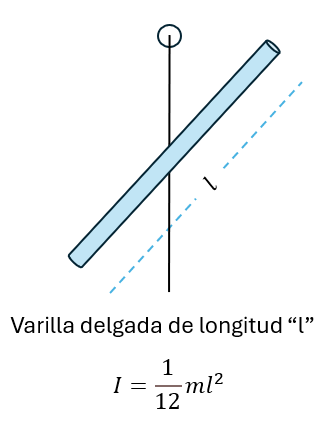
No debe confundirse con la fórmula del momento de inercia de una varilla donde el eje perpendicular cruza en uno de sus extremos, porque en ese caso, utilizaremos la fórmula:

$\displaystyle I=\frac{1}{3}m{{l}^{2}}$

En esta configuración, toda la masa de la varilla está distribuida a un solo lado del eje de rotación, aumentando el momento de inercia porque las partículas más alejadas del eje contribuyen más al valor de $\displaystyle I$

Momento de inercia de un disco o cilindro sólido

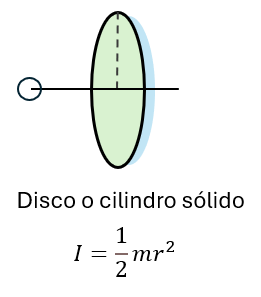
Momento de inercia de una esfera hueca

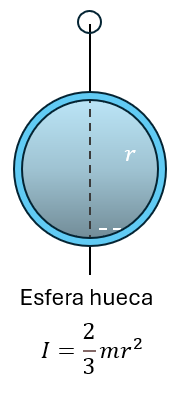
Entonces podemos empezar a resumir que el momento de inercia, o inercia rotacional, mide qué tan difícil es cambiar el movimiento de rotación de un objeto. A diferencia de la inercia lineal, que solo depende de la masa, el momento de inercia también depende de cómo está distribuida la masa alrededor del eje de rotación.

🔧 Aplicaciones del Momento de Inercia en la vida Real

Algo que muchos de nuestros usuarios nos han preguntado en el canal de whatsapp, es que incluyeramos las aplicaciones reales de ciertos fenómenos físicos, en este caso  sobre el momento de inercia, aunque puede parecer un concepto puramente teórico, tiene una amplia variedad de aplicaciones prácticas.

Diseño de Vehículos y Transporte 🚗

El momento de inercia es crucial en el diseño de automóviles, trenes, aviones y otros vehículos. Algunos ejemplos son:

• Ruedas de automóviles: El diseño de las llantas considera el momento de inercia para equilibrar la aceleración, el frenado y la eficiencia del combustible. Ruedas con menor momento de inercia permiten una aceleración más rápida.
• Motores y volantes de inercia: Los volantes de inercia en los motores de combustión interna almacenan energía cinética para suavizar el funcionamiento del motor, asegurando que siga girando entre explosiones.
• Control de estabilidad en trenes y aviones: En vehículos como trenes de alta velocidad o aviones, el análisis del momento de inercia ayuda a calcular la estabilidad y diseñar sistemas de control que eviten vuelcos o desestabilizaciones.

Construcción y estructuras 👷‍♂️

En el campo de la ingeniería civil y la arquitectura, el momento de inercia se utiliza para analizar la resistencia de vigas y columnas en estructuras.

• Diseño de puentes y edificios: En el análisis estructural, el momento de inercia se usa para predecir cómo reaccionarán los materiales a fuerzas externas, como vientos o terremotos. Esto garantiza que las estructuras sean seguras y soporten las cargas.
• Elementos rotativos en grúas: Las grúas giratorias y otros sistemas mecánicos de construcción dependen de un diseño óptimo del momento de inercia para asegurar movimientos estables y precisos.

Dentro del Deporte 🎾

El momento de inercia juega un papel importante en el diseño de equipamiento deportivo:

• Raquetas, palos de golf y bates de béisbol: Se diseña el momento de inercia para mejorar el control y la potencia. Por ejemplo, las raquetas con un momento de inercia más alto generan golpes más fuertes, pero requieren más esfuerzo para maniobrarlas.
• Patinaje artístico y gimnasia: Los atletas ajustan sus posiciones corporales para cambiar su momento de inercia. Por ejemplo, al acercar los brazos al cuerpo en un giro, disminuyen su momento de inercia y aumentan la velocidad de rotación.

Robótica y Automatización 🤖

En el diseño de robots y sistemas automatizados, el momento de inercia es esencial para calcular:

• Movimientos precisos de brazos robóticos: Se necesita un control exacto del momento de inercia para que los robots puedan mover herramientas o manipular objetos sin errores.
• Drones y sistemas autónomos: En los drones, el análisis del momento de inercia garantiza una rotación estable, permitiendo maniobras precisas y equilibradas en el aire.

Y si quisiéramos dando más ejemplos encontraríamos más y más en ámbitos por ejemplo en la energía y maquinaria industrial, en la astronomía y exploración espacial, así como en la biomédica, y biomecánica. Pero creo que queda más que claro cuál es el verdadero propósito del momento de inercia.

📓 Ejercicios Resueltos de Momento de Inercia

Solución:

Si revisamos los momentos de inercia para cada objeto, nos daremos cuenta que en un anillo cilíndrico uniforme la expresión matemática corresponde a la siguiente fórmula:

$\displaystyle I=m{{r}^{2}}$

Sustituimos los datos que nos proporciona el ejercicio:

$\displaystyle I=\left( {0.5kg} \right){{\left( {0.6m} \right)}^{2}}=0.18kg\cdot {{m}^{2}}$

Por lo que el resultado sería de 0.18 kg m²

Solución:

Como podemos observar, ahora se trata de una varilla delgada, esto quiere decir que la fórmula que vamos a aplicar será la siguiente:

$\displaystyle I=\frac{1}{{12}}m{{l}^{2}}$

Sustituyendo nuestros datos en la fórmula:

$\displaystyle I=\frac{1}{{12}}m{{l}^{2}}=\frac{1}{{12}}\left( {5kg} \right){{\left( {0.9m} \right)}^{2}}=0.338kg\cdot {{m}^{2}}$

Por lo que el momento de inercia será de 0.338 kg m²

Solución:

Nuevamente, veamos que para aplicar el momento de inercia en una esfera sólida, tendremos que recurrir a la siguiente fórmula:

$\displaystyle I=\frac{2}{5}m{{r}^{2}}$

Sustituyendo nuestros datos en la fórmula, obtenemos:

$\displaystyle I=\frac{2}{5}\left( {10kg} \right){{\left( {0.15m} \right)}^{2}}=0.09kg\cdot {{m}^{2}}$

Entonces, decimos que el momento de inercia de una esfera es de 0.09 kg m²

Solución:

Para un cilindro sólido homogéneo que gira alrededor de su eje central, la fórmula del momento de inercia es:

$\displaystyle I=\frac{1}{2}m{{r}^{2}}$

Sustituyendo los valores proporcionados:

$\displaystyle I=\frac{1}{2}\left( {8kg} \right){{\left( {0.25} \right)}^{2}}=0.25kg\cdot {{m}^{2}}$

Por lo tanto, el momento de inercia del cilindro es de 0.25 kg m²

Solución:

Para un disco delgado que gira alrededor de su eje central, usamos la fórmula:

$\displaystyle I=\frac{1}{2}m{{r}^{2}}$

Sustituyendoo los datos que tenemos del problema:

$\displaystyle I=\frac{1}{2}\left( {3kg} \right){{\left( {0.4m} \right)}^{2}}=0.24kg\cdot {{m}^{2}}$

Por lo tanto, el momento de inercia del disco es de 0.24 kg m²

Solución:

Para una varilla delgada que gira alrededor de un eje en uno de sus extremos, usamos la fórmula:

$\displaystyle I=\frac{1}{3}m{{l}^{2}}$

Sustituyendo los valores proporcionados:

$\displaystyle I=\frac{1}{3}\left( {4kg} \right){{\left( {1.2m} \right)}^{2}}=1.92kg\cdot {{m}^{2}}$

Por tanto, el momento de inercia es 1.92 kg m²

Solución:

Para un cilindro hueco, el momento de inercia está dado por:

$\displaystyle I=\frac{1}{2}m\left( {{{r}^{2}}_{{externo}}+{{r}^{2}}_{{interno}}} \right)$

Sustituyendo los valores del problema:

$\displaystyle I=\frac{1}{2}\left( {6kg} \right)\left[ {{{{\left( {0.4m} \right)}}^{2}}+{{{\left( {0.2m} \right)}}^{2}}} \right]$

Obtenemos:

$\displaystyle I=\frac{1}{2}\left( 6 \right)\left[ {0.016+0.04} \right]=\frac{1}{2}\left( 6 \right)\left( {0.2} \right)=0.6kg\cdot {{m}^{2}}$

Por lo tanto, el momento de inercia del cilindro hueco es de 0.6 kg m²