Momento de una Fuerza - Ejercicios Resueltos

Hoy hablaremos sobre el momento de una fuerza o también conocida como torque (τ) , este principio se define como el efecto de giro que es producida por una fuerza (F) y la distancia perpendicular (d) desde la línea de acción del objeto que se está girando.

La unidad del momento en el sistema internacional de unidades (SI) está dada por Newton-metro (Nm), y está definida como una cantidad vectorial.

Su dirección está dada por la regla de la mano derecha, que es perpendicular al plano de la fuerza y el punto del objeto que es paralelo al eje de rotación.

Fórmula del Momento de una Fuerza

La fórmula del Momento de una fuerza está dada por la siguiente fórmula:

Dónde:

M = es el momento de fuerza/torque.

F = es la fuerza ejercida sobre el objeto

d = es la distancia perpendicular desde la línea de acción de la fuerza hasta el objeto.

Nota: Cuando hay varias fuerzas actuando sobre un cuerpo, los momentos con respecto a un punto se pueden sumar siempre que se especifique una dirección positiva (horaria o antihoraria) y se considere para cada momento.

Ejercicios Resueltos de Momento de una Fuerza

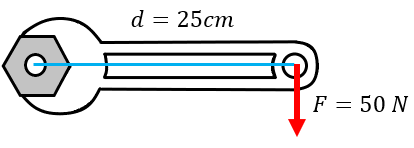
Solución:

Lo primero será anotar nuestros datos:

$\displaystyle d=25cm$

$\displaystyle F=50N$

$\displaystyle M=?$

Convirtiendo los 25 cm a metros

$\displaystyle 25cm\left( {\frac{{1m}}{{100cm}}} \right)=0.25m$

Aplicando la fórmula

$\displaystyle M=F\times d$

Sustituyendo datos

$\displaystyle M=50N\times 0.25m=12.5Nm$

Es decir:

Que sería nuestro momento.

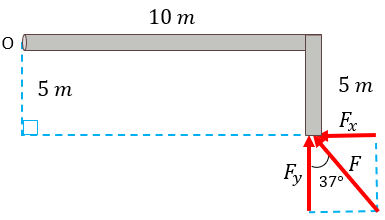
Solución:

Este problema implica descomponer previamente la fuerza F en una componente horizontal y una componente vertical y luego poder determinar el momento producido por cada una de estas y finalmente sumar algebraicamente estos.

$\displaystyle {{F}_{x}}=100Nsen37{}^\circ =60.18N$

$\displaystyle {{F}_{y}}=100N\cos 37{}^\circ =79.86N$

Si aplicamos el momento en "x", estaría dado por la fuerza en "X" y su linea de acción vertical de 5m, es decir:

$\displaystyle {{M}_{x}}={{F}_{x}}\times d=60.18N\times 5m=-300.9Nm$

Pero el resultado sería negativo esto es porque la acción de esta fuerza va en sentido de las manecillas del reloj ↩

Para poder obtener el momento generado en "y", aplicamos:

$\displaystyle {{M}_{y}}={{F}_{y}}\times d=79.86N\times 10m=798.6Nm$

En este caso el momento sería positivo puesto que la acción de la fuerza va en contra de las manecillas del reloj ↪

Ahora es momento de obtener la resultante de todos los momentos:

$\displaystyle {{M}_{R}}=-300.9Nm+798.6Nm=497.7Nm$

Obteniendo así el momento resultante, que es el momento producido por la fuerza F que es la resultante de las componentes F_x y F_y

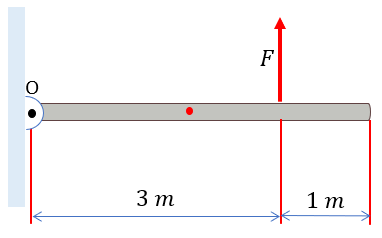
Solución:

El diagrama de cuerpo libre de este problema estará dado de la siguiente manera:

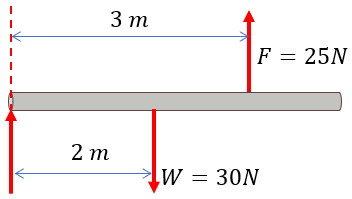
Observe que solamente tendremos que aplicar el momento tanto en la fuerza, como en el peso para poder obtener el valor del momento resultante en el punto O.

Aplicamos el momento realizado por la fuerza:

$\displaystyle {{M}_{F}}=F\times d=25N\times 3m=75Nm$

El momento será positivo, porque va contra las manecillas del reloj, es decir anti-horario.

Ahora, apliquemos el momento generado por el peso de la barra:

$\displaystyle {{M}_{W}}=F\times d=30N\times 2m=60Nm$

El momento del peso será negativo debido a que el momento va en dirección horaria de las manecillas del reloj.

Ahora obtenemos la resultante:

$\displaystyle {{M}_{R}}=75Nm-60Nm=15Nm$

Como el momento resultante de las fuerzas respecto al punto O es positivo, la barra experimentará un efecto de rotación en sentido anti-horaro.

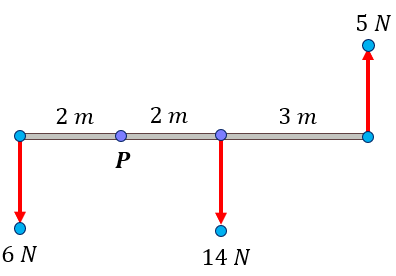
Solución:

Cada fuerza está perpendicular al punto P, por lo que haremos el cálculo de mometos de izquierda a derecha.

$\displaystyle {{M}_{1}}=F\times d=6N\times 2m=12Nm$

El primer momento será positivo, porque va en sentido contrario de las agujas del reloj respecto a P

$\displaystyle {{M}_{2}}=F\times d=14N\times 2m=-28Nm$

El segudo momento será negativo, porque va en sentido de las agujas del reloj

$\displaystyle {{M}_{3}}=F\times d=5N\times 5m=25Nm$

El tercer momento será positivo, porque va en sentido contrario de las agujas del reloj

Ahora realazmos la suma total:

$\displaystyle {{M}_{R}}=12Nm-28Nm+25Nm=9Nm$

Por lo que el valor resultante es de 9Nm en sentido contrario a las manecillas del reloj.

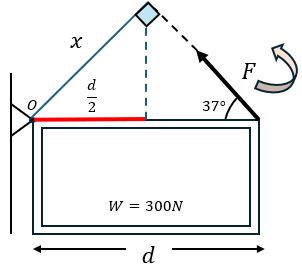
Solución:

Lo primero que haremos será realizar la ecuación de momentos para este problema en O.

$\displaystyle -W\left( {\frac{d}{2}} \right)+Fsen37{}^\circ \cdot d=0$

$\displaystyle -300\left( {\frac{d}{2}} \right)+Fsen\left( {0.602} \right)\cdot d=0$

dividiendo todo por "d"

$\displaystyle -150N+0.602F=0$

$\displaystyle F=\frac{{150N}}{{0.602N}}=249.17N$

Por lo tanto la fuerza para que la pizarra esté en equilibrio, es de F = 249.17 N