Movimiento Circular - Ejercicios Resueltos

Estimados lectores, nuevamente seguimos publicando acerca de los temas de Física y de como entenderlos sin tener ninguna dificultad, en esta ocasión nos toca hablar de uno de los temas que más confunde a los estudiantes, y se trata del movimiento circular. Bien expliquemos de que se trata este movimiento y todo sus derivados:

🤔 ¿Qué es el movimiento circular?

El movimiento circular es un movimiento que está relacionado con la misma naturaleza, desde el movimiento de los planetas alrededor del sol, o el movimiento de la tierra sobre sí misma, el movimiento de un balón al golpearlo, el movimiento de las llantas de algún móvil. Como vemos hay muchas formas de ejemplo para poder explicar lo que es el movimiento circular. Una de las grandes cosas que caracteriza a éste movimiento es que al ser un movimiento repetitivo, se le clasifica como periódico.

El movimiento circular se realiza sobre dos dimensiones, tal como se ha hecho con el movimiento parabólico, y tiro horizontal.

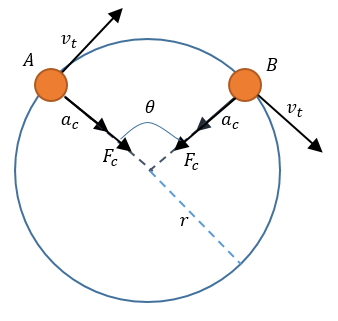
Pero debemos preguntarnos ¿cómo se produce el movimiento circular?, y la respuesta es interesante, el movimiento circular se genera cuando una fuerza externa fuera del cuerpo llamada centrípeta, describe una forma perpendicular a la trayectoria que describe el movimiento. Aquí se involucra el eje de rotación como origen del sistema, y varía de acuerdo al sentido de la dirección del vector.

El Concepto de Periodo Y Frecuencia

Para entender aún más a éste movimiento, es importante tener en cuenta los siguientes dos conceptos. El periodo y la frecuencia.

Periodo: Periodo "T" es el tiempo que le toma a un cuerpo dar una vuelta completa.

$\displaystyle T=\frac{s}{ciclo}$

Frecuencia: La frecuencia se define como el número de vueltas completas, revoluciones o ciclos que puede efectuar un cuerpo en unidad de tiempo. Sus unidades son los Hertz (Hz), Por ejemplo, si un cuerpo presenta 1 Hz, entonces estamos hablando de que realiza una vuelta completa.

$\displaystyle f=\frac{ciclo}{s}$

En algunos textos de Física, también encontraremos que muchas veces para referirse a la expresión de frecuencia se hace mediante los RPM = Revoluciones por Minuto, que prácticamente necesitaremos convertir a ciclos por segundo para expresarlo en el Sistema Internacional.

El desplazamiento angular y el radian

El desplazamiento angular de un objeto lo describe la cantidad de rotación y se representa por el ángulo formado al girar el cuerpo de un punto A a un punto B, tal como se ve en la imagen de arriba.

Por otra parte tenemos al radian, que representa una magnitud geométrica y adimensional, no posee unidades, es el cociente entre dos longitudes, el arco simbolizado con la letra “S” y el radio “r”,

La velocidad angular

La velocidad angular se define como el desplazamiento angular por unidad de tiempo, suele ser una cantidad vectorial, o sea que posee magnitud, dirección y sentido. Dicha velocidad angular tiene tres fórmulas que pueden usarse para los problemas que estaremos realizando en nuestro tema.

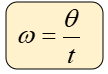
Dónde:

ω = velocidad anguar (rad/s)

θ = desplazamiento angular (rad)

t = tiempo (s)

Otra forma de calcular la velocidad angular, es mediante esta otra fórmula.

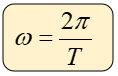
Dónde:

ω = velocidad anguar (rad/s)

π = 3.1416 rad

T = segundos / ciclos

Por ende, podemos decir que la tercera forma para calcular la velocidad angular, es mediante la siguiente expresión:

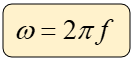
La aceleración angular

La aceleración se define como aquella variación que sufre la velocidad angular por unidad de tiempo:

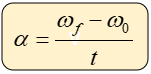
Dónde:

α = aceleración angular (rad/s²)

Velocidad Tangencial

La velocidad tangencial es un tipo de velocidad lineal que se presenta solo en el extremo de la trayectoria del movimiento que describe. Se puede decir que es un vector siempre perpendicular al vector posición radio.

El valor de la velocidad tangencial es de gran importancia porque nos aporta la seguridad de la rapidez con la que gira un cuerpo y la velocidad que ésta tendría si saliera disparado. Por ecuación lo podemos encontrar de la siguiente forma:

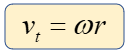
Dónde:

r = radio (m)

También podemos encontrarlo de la siguiente forma:

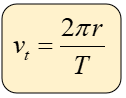
O también como:

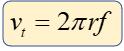
Aceleración Tangencial

La definición de la aceleración tangencial, hace referencia a la variación de velocidad lineal o tangencial, puesto que corresponde a un movimiento circular variado o movimiento circular uniformemente variado (MCUA).

Aceleración Centrípeta

La aceleración centrípeta es una aceleración que siempre está presente, es la causante de que la velocidad tangencial, localizada en la parte del contorno de la circunferencia cambie repentinamente de dirección y sentido, aunque ésta no influya en su valor. Por lo general éste tipo de aceleración es perpendicular a la velocidad tangencial. Dada por las siguientes dos fórmulas:

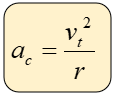
o también como:

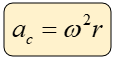
La Aceleración Resultante

Si el movimiento circular es variado se presentan tanto la aceleración tangencial, como la aceleración centrípeta, por lo que si requerimos calcular la aceleración resultante, tendremos que hacerlo mediante la siguiente fórmula:

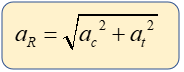
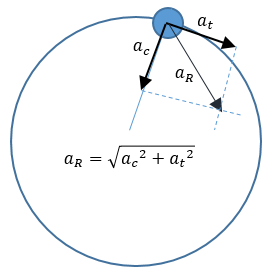
Fuerza Centrípeta

La fuerza centrípeta es una fuerza que está dirigida hacía el centro del movimiento circular, deducida por las leyes de Newton, posee la siguiente ecuación:

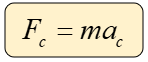
Dónde:

m = masa (kg)

También podemos encontrarla mediante la siguiente fórmula:

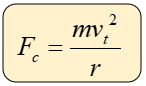
Fuerza Centrífuga

La fuerza centrífuga nunca actúa sobre el cuerpo, actúa sobre la tensión que hace girar al cuerpo, no hay que confundirse con esta definición, Su tensión aumenta mientras incrementa la velocidad de rotación.

🔸 Ejercicios Resueltos del Movimiento Circular

Solución:

El problema es muy fácil de resolver y analizar, primero porque nos explica que la hélice de la turbina adquiere una velocidad final de 6500 rad/s y nos proporciona el tiempo. La pregunta es la magnitud de la aceleración angular, y si sabemos aplicar correctamente la fórmula, daremos con el resultado. ¿Qué fórmula usaremos?

$\displaystyle \alpha =\frac{{{\omega }_{f}}}{t}$

Sustituyendo nuestros datos en la fórmula:

$\displaystyle \alpha =\frac{{{\omega }_{f}}}{t}=\frac{6500\frac{rad}{s}}{4s}=1625\frac{rad}{{{s}^{2}}}$

Por lo que la magnitud de la aceleración angular fue de 1625 rad/s²

Solución:

El problema es muy claro, y nos piden a resolver dos incisos, tanto la aceleración media, así como la magnitud de su desplazamiento angular. Entonces comencemos a resolver 😀

a) Obteniendo la aceleración media

Para la aceleración media, usamos la siguiente fórmula:

$\displaystyle {{\alpha }_{m}}=\frac{{{\omega }_{f}}-{{\omega }_{0}}}{t}$

Sustituyendo nuestros datos en la fórmula:

$\displaystyle {{\alpha }_{m}}=\frac{{{\omega }_{f}}-{{\omega }_{0}}}{t}=\frac{220\frac{rad}{s}-50\frac{rad}{s}}{0.9s}=188.9\frac{rad}{{{s}^{2}}}$

Qué sería nuestra aceleración media, 188.9 rad/s²

b) Obteniendo el desplazamiento angular en ese tiempo

La fórmula que usaremos para el desplazamiento angular en el determinado tiempo, será la siguiente:

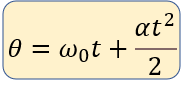
$\displaystyle \theta ={{\omega }_{0}}t+\frac{\alpha {{t}^{2}}}{2}$

Sustituyendo nuestros datos en la fórmula:

$\displaystyle \theta =\left( 50\frac{rad}{s} \right)\left( 0.9s \right)+\frac{\left( 188.9\frac{rad}{{{s}^{2}}} \right){{\left( 0.9s \right)}^{2}}}{2}=45rad+76.5rad=121.5rad$

Es decir que el desplazamiento es de 121.5 radianes

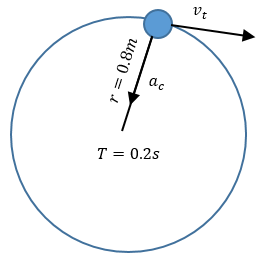
Solución: Vamos a utilizar las fórmulas expuestas en cada definición, así que prestar mucha atención. Porque será de gran relevancia.

Nuestros datos son:

r = 0.8 m

T = 0.2 s

a) Calculando la Velocidad Angular

Para calcular la velocidad angular, podemos usar la siguiente fórmula, que relaciona solamente al periodo.

$\displaystyle \omega =\frac{2\pi }{T}=\frac{2(3.1416)rad}{0.2s}=31.42\frac{rad}{s}$

b) Calculando la velocidad tangencial 

Para poder obtener la velocidad tangencial, aplicamos la fórmula y sustituimos los datos.

$\displaystyle {{v}_{t}}=\frac{2\pi r}{T}=\frac{2(3.1416)\left( 0.8m \right)}{0.2s}=25.13\frac{m}{s}$

c) Calculando la aceleración tangencial

Para obtener la aceleración tangencial, necesitamos saber la aceleración angular, para ello aplicamos la fórmula:

$\displaystyle \alpha =\frac{\omega }{t}=\frac{31.42\frac{rad}{s}}{0.2s}=157.1\frac{rad}{{{s}^{2}}}$

Ahora si aplicamos la fórmula de la aceleración tangencial.

$\displaystyle {{a}_{t}}=\alpha r=\left( 157.1\frac{rad}{{{s}^{2}}} \right)\left( 0.8m \right)=125.68\frac{m}{{{s}^{2}}}$

d) Calculando la aceleración centrípeta. 

Para obtener la aceleración centrípeta, aplicamos la siguiente fórmula y sustituimos datos:

$\displaystyle {{a}_{c}}=\frac{{{v}_{t}}^{2}}{r}=\frac{{{\left( 25.13\frac{m}{s} \right)}^{2}}}{0.8m}=789.4\frac{m}{{{s}^{2}}}$

una aceleración demasiado grande.

e) Calculando la velocidad resultante

Aplicamos la siguiente fórmula:

$\displaystyle {{a}_{R}}=\sqrt{{{a}_{c}}^{2}+{{a}_{t}}^{2}}=\sqrt{{{\left( 789.4\frac{m}{{{s}^{2}}} \right)}^{2}}+{{\left( 125.68\frac{m}{{{s}^{2}}} \right)}^{2}}}=799.34\frac{m}{{{s}^{2}}}$

Y con este resolvemos el ejercicio 😎

Solución: El problema es más sencillo que el ejemplo anterior, ya que solamente nos piden la aceleración centrípeta, para obtener dicha aceleración necesitamos conocer la velocidad tangencial, y posteriormente la aceleración centrípeta. 

$\displaystyle {{v}_{t}}=\frac{2\pi r}{T}=\frac{2(3.1416)\left( 0.35m \right)}{0.4s}=5.5\frac{m}{s}$

Ahora si podemos calcular la aceleración centrípeta.

$\displaystyle {{a}_{c}}=\frac{{{v}_{t}}^{2}}{r}=\frac{{{\left( 5.5\frac{m}{s} \right)}^{2}}}{0.35m}=86.43\frac{m}{{{s}^{2}}}$

Y listo problema resuelto 😀

Solución: En este ejemplo a diferencia de los anteriores, poseemos una masa de la piedra, y es lógico, porque queremos encontrar una fuerza, y sabemos que por la segunda ley de Newton, para obtener la fuerza es necesario una masa.

Aplicamos la fórmula:

$\displaystyle {{F}_{c}}=\frac{\left( m \right){{\left( {{v}_{t}} \right)}^{2}}}{r}=\frac{\left( 0.06kg \right){{\left( 9\frac{m}{s} \right)}^{2}}}{0.75m}=6.48N$

y listo, hemos obtenido la fuerza centrípeta.

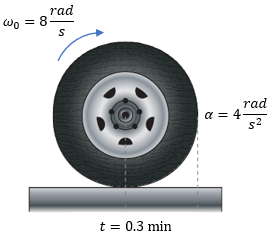
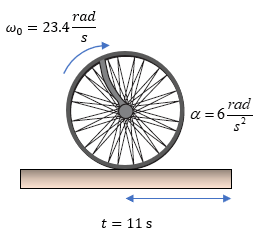
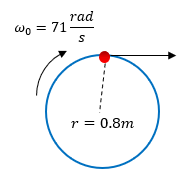
📃 Ejercicios para Practicar del Movimiento Circular 

Para mejorar el aprendizaje del tema de movimiento circular, puede resolver los siguientes ejercicios y en caso de dudas, puede ver la solución. 😊👇

👉 Ver Solución

👉 Ver Solución

👉 Ver Solución