Notación Científica - Ejercicios Resueltos
Dentro de la física es normal que utilicemos la notación científica para expresar cantidades, pero ¿qué es la notación científica?, la notación científica es una forma especial de escribir números en el ámbito de la ciencia, por lo general se utiliza para escribir números que son muy grandes o pequeños. La notación científica también puede ser llamada como notación exponencial.
La notación científica es útil porque permite escribir números de manera más compacta, esto favorece simplificar las operaciones matemáticas al momento de expresar alguna cantidad que podamos utilizar al momento de resolver problemas de física, la base esencial para este tema es sin duda las potencias de base 10, aquí aprenderemos a resolver ejercicios y ejemplos de notación científica paso a paso.
El ser humano es muy pequeño comparado con las estrellas, el cosmos, y a la vez, muy grande comparado con los átomos. Sin embargo, el rango o intervalo de dimensiones y distancias del mundo físico que el hombre ha podido determinar científicamente mediante sus investigaciones es impresionante. Esto significa que en las mediciones científicas, los valores medidos pueden ser mucho mayores o mucho menores que los que se pueden medir directamente. ?
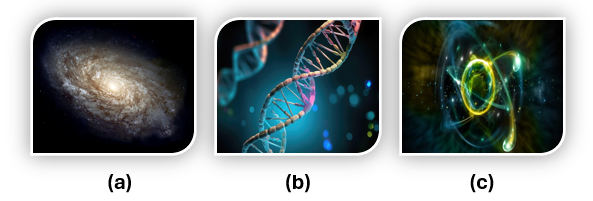
La notación científica sirve para escribir cantidades con dimensiones sumamente grandes como las de las (a) galaxias o tan pequeñas como las de (b) las moléculas de ADN y (c) las partículas subatómicas.
¿Cómo se usa la notación científica?
Como en la Física es necesario hacer cálculos tanto con números muy grandes como con números muy pequeños, se ha buscado una notación práctica para expresarlos. La solución consiste en usar las potencias de diez. La manera de escribir los números que representan el resultado de una medición por medio de potencias de diez se llamana notación científica. Para dar comienzo a este tema, es importante que comprendamos las potencias de base 10 y el beneficio de uso, recordemos que, si un número se eleva a una potencia, la potencia nos indicará las veces que el número se multiplica por si mismo, por ejemplo:
a) $\displaystyle {{6}^{2}}=6\times 6$
b) $\displaystyle {{9}^{3}}=9\times 9\times 9$
c) $\displaystyle {{2}^{5}}=2\times 2\times 2\times 2\times 2$
Pero en el caso de las potencias de base 10, siempre será el número 10 el que se eleve a una potencia indicada, por ejemplo:
$\displaystyle {{10}^{1}}=10$
$\displaystyle {{10}^{2}}=10\times 10=100$
$\displaystyle {{10}^{3}}=10\times 10\times 10=1000$
$\displaystyle {{10}^{4}}=10\times 10\times 10\times 10=10000$
$\displaystyle {{10}^{5}}=10\times 10\times 10\times 10\times 10=100000$
$\displaystyle {{10}^{6}}=10\times 10\times 10\times 10\times 10\times 10=1000000$
Si observas cada caso particular, podrás encontrar que cuando la base 10 está elevada a una potencia, el resultado es igual al número 1 seguido de tantos ceros como se indica en la potencia, ¿si lo observas?, volvamos a ver otro ejemplo:
$\displaystyle {{10}^{7}}=10000000$
107 es igual a 1 seguido de 7 ceros.
Esto mismo ocurre si hacemos la operación ahora con una potencia negativa. Esto equivale a dividir 1 entre 10 elevado a esa misma potencia, pero con un signo positivo. Por ejemplo:
a) $\displaystyle {{10}^{{-1}}}=\frac{1}{{10}}=0.1$
b) $\displaystyle {{10}^{{-2}}}=\frac{1}{{100}}=0.01$
c) $\displaystyle {{10}^{{-3}}}=\frac{1}{{1000}}=0.001$
d) $\displaystyle {{10}^{{-4}}}=\frac{1}{{10000}}=0.0001$
e) $\displaystyle {{10}^{{-5}}}=\frac{1}{{100000}}=0.00001$
Al observar en esta situación podemos darnos cuenta de que la base 10 está elevada a una potencia negativa, el resultado es igual a recorrer el punto decimal a partir del número 1 tantas veces como lo señale la potencia negativa. Por ejemplo:
$\displaystyle {{10}^{{-9}}}=0.000000001$
El punto decimal se recorrió a la izquierda 9 cifras a partir del 1.
Multiplicar y Dividir Potencias de Diez
Un exponente es el número positivo o negativo, que indica a qué potencia se eleva una base. En la notación científica, la base es el número diez. Para las operaciones con potencias de 10, valen algunas reglas simples, que hay que tomar en cuenta:
- Al multiplicar dos potencias de 10, el resultado es la potencia de 10 cuyo exponente es igual a la suma de los exponentes. Por ejemplo:
$\displaystyle {{10}^{3}}\times {{10}^{5}}={{10}^{{3+5}}}={{10}^{8}}$
$\displaystyle {{10}^{{-6}}}\times {{10}^{2}}={{10}^{{-6+2}}}={{10}^{{-4}}}$
- Al dividir dos potencias de 10, el resultado es la potencia de 10 cuyo exponente es igual a la resta de los exponentes del numerador y del denominador. Por ejemplo:
$\displaystyle \frac{{{{{10}}^{7}}}}{{{{{10}}^{3}}}}={{10}^{{7-3}}}={{10}^{4}}$
$\displaystyle \frac{{{{{10}}^{{-3}}}}}{{{{{10}}^{{-8}}}}}={{10}^{{-3-(-8)}}}={{10}^{{-3+8}}}={{10}^{5}}$
Operaciones con Notación Científica
En física es indispensable el buen uso de la notación científica. Esto implica de alguna forma poder utilizar o emplear correctamente las cuatro operaciones fundamentales de la aritmética, es decir, el saber sumar, restar, multiplicar y dividir.
- Para sumar o restar cantidades expresadas en notación científica, es necesario que ambas cantidades estén escritas en términos de la misma potencia de 10. Una vez que esta condición se cumpla para ambas cantidades, solamente deben sumarse las cantidades que están multiplicadas en cada potencia de 10.
Solución:
Si observamos en este primer ejemplo, no hay dificultad en llevar a cabo las operaciones, porque ambas bases están elevadas a la misma potencia, por lo tanto solo sumamos las cantidades, es decir:
$\displaystyle \left( {3\times {{{10}}^{5}}} \right)+\left( {5\times {{{10}}^{5}}} \right)=8\times {{10}^{5}}$
Solución:
Para efectuar esta resta, primero es necesario que ambas cantidades tengan la misma potencia de 10. Es decir, que en este caso haremos lo siguiente:
$\displaystyle 8.1\times {{10}^{5}}=8.1\times 10\times 10\times {{10}^{3}}=810\times {{10}^{3}}$
Como ahora 810 ya está expresada en la misma potencia de 10, que la otra cantidad, ya podemos efectuar la operación:
$\displaystyle \left( {8.1\times {{{10}}^{5}}} \right)-\left( {2\times {{{10}}^{3}}} \right)=808\times {{10}^{3}}$
Ahora solo resta convertir correctamente el resultado a una notación científica adecuada:
$\displaystyle 808\times {{10}^{3}}=8.08\times 10\times 10\times {{10}^{3}}=8.08\times {{10}^{5}}$
- Para multiplicar cantidades expresadas en notación científica, simplemente hay que multiplciar por separado las potencias de 10 y las cantidades que se encuentran multiplicadas por dichas potencias.
Solución:
Para este ejemplo, no hace falta explicar a detalle el procedimiento, bastará con el análisis.
$ \displaystyle \left( {2\times {{{10}}^{5}}} \right)\cdot \left( {3\times {{{10}}^{4}}} \right)=\left( {2\cdot 3} \right)\times \left( {{{{10}}^{5}}\cdot {{{10}}^{4}}} \right)=6\times {{10}^{9}}$
Solución:
$\displaystyle \left( {4.7\times {{{10}}^{5}}} \right)\cdot \left( {3.7\times {{{10}}^{7}}} \right)=\left( {4.7\cdot 3.7} \right)\times \left( {{{{10}}^{5}}\cdot {{{10}}^{7}}} \right)=17.39\times {{10}^{{12}}}$
- Para efectuar o llevar a cabo la división con notación científica sigue las mismas reglas que la multiplicación, justo como se muestra a continuación.
Solución:
$\displaystyle \frac{{8\times {{{10}}^{5}}}}{{4\times {{{10}}^{{11}}}}}=\left( {\frac{8}{4}} \right)\times \left( {\frac{{{{{10}}^{5}}}}{{{{{10}}^{{11}}}}}} \right)=2\times {{10}^{{-6}}}$
Solución:
$\displaystyle \frac{{9.5\times {{{10}}^{8}}}}{{2.8\times {{{10}}^{{-4}}}}}=\left( {\frac{{9.5}}{{2.8}}} \right)\times \left( {\frac{{{{{10}}^{8}}}}{{{{{10}}^{{-4}}}}}} \right)=3.39\times {{10}^{{12}}}$
Ejercicios Resueltos de Notación Científica
Ahora es momento de ver algunos ejemplos de notación científica y entender por completo este tema 😀
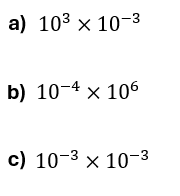
Solución:
Recordemos que la multiplicación de potencias de la misma base, sus exponentes se suman.
a)
$\displaystyle {{10}^{3}}\times {{10}^{{-3}}}={{10}^{{3+(-3)}}}={{10}^{{3-3}}}={{10}^{0}}$
b)
$\displaystyle {{10}^{{-4}}}\times {{10}^{6}}={{10}^{{-4+6}}}={{10}^{2}}$
c)
$\displaystyle {{10}^{{-3}}}\times {{10}^{{-3}}}={{10}^{{-3+(-3)}}}={{10}^{{-3-3}}}={{10}^{{-6}}}$
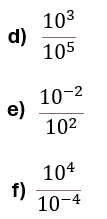
Recordemos que la división de potencias de la misma base, sus exponentes se restan.
d)
$\displaystyle \frac{{{{{10}}^{3}}}}{{{{{10}}^{5}}}}={{10}^{{3-5}}}={{10}^{{-2}}}$
e)
$\displaystyle \frac{{{{{10}}^{{-2}}}}}{{{{{10}}^{2}}}}={{10}^{{-2-2}}}={{10}^{{-4}}}$
f)
$\displaystyle \frac{{{{{10}}^{4}}}}{{{{{10}}^{{-4}}}}}={{10}^{{4-(-4)}}}={{10}^{{4+4}}}={{10}^{8}}$
Solución:
Como observamos, 630 000 consta de seis cifras enteras; para expresarlo con una sola cifra entera, debemos recorrer el punto decimal cinco veces:
![]()
Por tanto: 630 000 = 6.3 x 105
Como se observa, la base 10 está elevada a la 5ta. Potencia, pues fue el número de veces que recorrimos el punto decimal, esto es importante de analizar para poder entender los demás ejemplos.
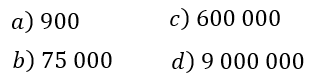
Solución:
Para el inciso a)
$\displaystyle 900=9x{{10}^{2}}$
(ya que recorrimos dos veces el punto)
Para el inciso b)
$\displaystyle 75000=7.5x{{10}^{4}}$
(ya que recorrimos cuatro veces el punto)
Para el inciso c)
$\displaystyle 600000=6x{{10}^{5}}$
(ya que recorrimos cinco veces el punto)
Para el inciso d)
$\displaystyle 9000000=9x{{10}^{6}}$
(ya que recorrimos seis veces el punto)
Solución:
Como observamos 0.000005 no tiene ninguna cifra entera, de manera que para expresarlo como tal debemos de recorrer el punto decimal seis veces, por tanto:
![]()
Como se detalla, la base 10 está elevada a la 6ta potencia, pues fue el número de veces que recorrimos el punto decimal. El signo negativo cuando convertimos una fracción decimal a entero.
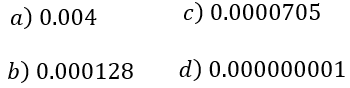
Solución:
Para el inciso a)
$\displaystyle 0.004=4x{{10}^{{-3}}}$
(ya que recorrimos tres veces el punto)
Para el inciso b)
$\displaystyle 0.000128=1.28x{{10}^{{-4}}}$
(ya que recorrimos cuatro veces el punto)
Para el inciso c)
$\displaystyle 0.0000705=7.05x{{10}^{{-5}}}$
(ya que recorrimos cinco veces el punto)
Para el inciso d)
$\displaystyle 0.000000001=1x{{10}^{{-9}}}$
(ya que recorrimos nueve veces el punto)
Ejercicios para practicar de Notación Científica
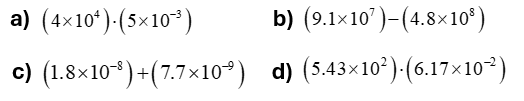
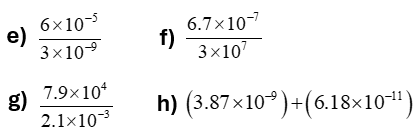
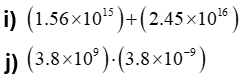
-
Me pareció genial para repasar antes de un examen , los temas se explican con claridad y objetividad
7 Deja tu comentario
Deja una respuesta

Estos temas te pueden interesar