Péndulo Simple - Ejercicios Resueltos

Ya que sabemos cómo funciona el movimiento armónico simple, es momento de entender como funciona el péndulo simple. Pero para comenzar, primero veamos, ¿qué es un péndulo simple?

Un péndulo simple está constituido por un cuerpo pesado que está suspendido en algún punto sobre un eje horizontal por medio de un hilo que posee masa despreciable. Cuando se separa un péndulo de su posición de equilibrio y después se suelta, oscila de un lado a otro por efecto de su peso. Tal como se aprecia en la siguiente imagen:

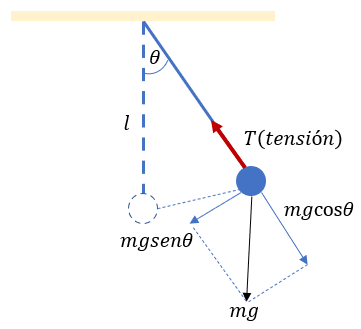
Se le coloca T a la tensión para no confundirla con la T del periodo que veremos a continuación.

Fórmula del Péndulo Simple

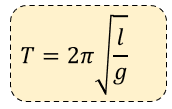
Dónde:

T = Periodo del péndulo en segundos (s)

l = longitud del péndulo en metros (m) (se mide desde el punto donde está suspendido hasta el centro de gravedad del cuerpo pesado que constituye al péndulo)

g = magnitud de la aceleración de la gravedad equivalente a 9.8 m/s^2

Es importante recalcar aquí dos leyes del péndulo muy vitales e importantes. ?

Leyes de los Péndulos

1. El periodo de las oscilaciones, por muy pequeñas que sean, no depende de la masa del péndulo ni de la amplitud del movimiento, sino únicamente de su longitud
2. El periodo es directamente proporcional a la raíz cuadrada de la longitud del péndulo, e inversamente proporcional a la raíz cuadrada de la magnitud de la aceleración debida a la acción de gravedad.

Ejercicios Resueltos de Péndulo Simple

Para entender mucho mejor el tema de péndulo simple, veamos algunos ejercicios.

Solución:

Lo primero que debemos de realizar, es anotar nuestros datos:

l = 45 cm = 0.45 m

g = 9.8 m/s^2

f = ?

Si verificamos los datos, podemos sustituir directamente en la fórmula:

$\displaystyle T=2\pi \sqrt{{\frac{l}{g}}}$

Sustituyendo

$\displaystyle T=2\left( {3.14} \right)\sqrt{{\frac{{0.45m}}{{9.8\frac{m}{{{{s}^{2}}}}}}}}=6.28\sqrt{{0.046}}=1.35s$

Obtenemos un periodo de 1.35 s

Pero como el problema nos pide frecuencia, entonces la convertimos con nuestro factor de conversión.

$\displaystyle f=\frac{1}{T}=\frac{1}{{1.35s}}=0.74\frac{{oscilaciones}}{s}$

Obtenemos 0.74 oscilaciones por cada segundo recorrido. 😀

Solución:

Este es uno de los problemas más interesantes por el resultado que vamos a obtener, sin embargo debemos de anotar los datos que tenemos, para ver cuál será nuestro resultado.

Datos:

T = 2s

g = 9.8 m/s^2

l = ?

Nuestra fórmula como bien sabemos es la siguiente:

$\displaystyle T=2\pi \sqrt{{\frac{l}{g}}}$

Pero el problema nos pide encontrar la longitud, por lo que tendremos que recurrir a un despeje.

$\displaystyle {{T}^{2}}={{\left( {2\pi \sqrt{{\frac{l}{g}}}} \right)}^{2}}$

$\displaystyle {{T}^{2}}=4{{\pi }^{2}}\left( {\frac{l}{g}} \right)$

Luego:

$\displaystyle l=\frac{{{{T}^{2}}g}}{{4{{\pi }^{2}}}}$

Ahora si podemos sustituir nuestros datos en la fórmula:

$\displaystyle l=\frac{{{{T}^{2}}g}}{{4{{\pi }^{2}}}}=\frac{{{{{\left( 2 \right)}}^{2}}\left( {9.8} \right)}}{{4{{{\left( {3.14} \right)}}^{2}}}}=\frac{{39.2}}{{39.44}}=0.99\approx 1m$

Y obtenemos la longitud del péndulo de 1 metro.

Grandioso, ¿no?

Solución:

Al igual que el ejercicio anterior, este problema es muy similar. Lo único que debemos hacer será replantear nuestros datos:

T = 1.2 s

g = 9.8 m/s^2

l = ?

Ahora si pensamos bien en el problema, nos daremos cuenta que necesitamos obtener la fórmula en términos de la longitud, por lo cual tomaremos la fórmula del ejercicio anterior, ya que previamente realizamos el despeje:

$\displaystyle l=\frac{{{{T}^{2}}g}}{{4{{\pi }^{2}}}}$

Ahora vamos a sustituir nuestros datos:

$\displaystyle l=\frac{{{{T}^{2}}g}}{{4{{\pi }^{2}}}}=\frac{{{{{\left( {1.2} \right)}}^{2}}\left( {9.8} \right)}}{{4{{{\left( {3.14} \right)}}^{2}}}}=\frac{{14.11}}{{39.43}}=0.357\approx 0.36m$

Por lo que obtenemos una longitud de 0.36 m aproximadamente.

Examen de Péndulo Simple

Ahora es momento de comprobar tus conocimientos teórico-prácticos de los péndulos.