Potencial Eléctrico - Ejercicios Resueltos

En este artículo hablaremos sobre la Energía Potencial Eléctrica, o Potencial Eléctrico, e incluso algunos autores manejan el término de Energía Potencial Electrostática, sea cualquiera de los términos, el estudio de este tema es de gran importancia para aprender por completo el término relacionado por el trabajo que realizan las cargas y cada una de las variables.

Contenidos

🤔 ¿Qué es la energía potencial eléctrica?
1. ⭐ Consideraciones del Potencial Eléctrico
⚡ Potencial Eléctrico en un punto de una Carga
🔋 Potencial Eléctrico Creado por Varias Cargas Puntuales
🔮 Superficies Equipotenciales
⭕ Diferencia de Potencial Eléctrico
🔸 Ejercicios Resueltos de Potencial Eléctrico

🤔 ¿Qué es la energía potencial eléctrica?

Considere un conductor electrizado positivamente, por ejemplo, con carga Q, fijo en un determinado lugar, libre de la influencia de otras cargas eléctricas. Ya sabemos que, en la región del espacio que envuelve ese cuerpo, existe un campo eléctrico generado por las cargas en él existentes.

Ahora, vamos a dejar en un punto P una carga de prueba q, también positiva, a una distancia d del conductor. Debido al campo eléctrico, la carga de prueba será repelida y se alejará del conductor, ganando velocidad y, consecuentemente, adquiriendo energía cinética (energía de movimiento). Observe que la carga q, si fuera negativa, sería atraída, y no repelida.

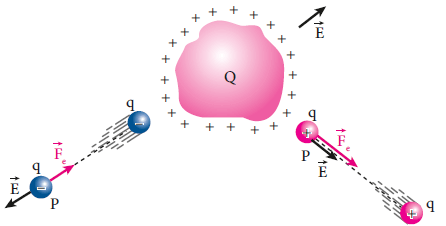
Potencial Eléctrico

Por adquirir energía cinética, podemos concluir que, en el punto P, la carga de prueba q almacena una energía potencial denominada energía potencial electrostática o eléctrica, que vamos a simbolizar por Ep.

Esta energía potencial se transforma, en consecuencia, en energía cinética. Así, podemos decir que la carga Q del conductor produce un campo eléctrico que también puede ser descrito por una magnitud escalar denominada potencial electrostático (o eléctrico).

Este potencial electrostático en el punto P traduce la energía potencial eléctrica almacenada por unidad de carga colocada en esa ubicación.

El potencial, simbolizado por V, se define por la expresión:

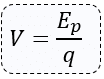
Fórmula de potencial eléctrico

En el SI (Sistema Internacional), la unidad de potencial eléctrico es el volt, de símbolo V, así denominado en homenaje a Alessandro Volta (1745-1827).

Como hemos visto:

$\displaystyle V=\frac{{{E}_{p}}}{q}$

Es decir:

$\displaystyle volt=\frac{joule}{coulomb}$

⭐ Consideraciones del Potencial Eléctrico

En realidad, la energía potencial es adquirida por el sistema Q y q. Si estas dos cargas pueden moverse, ellas obtendrán energía cinética a partir de esa energía potencial. Cuando, sin embargo, la carga Q es fija (lo que ocurre la mayoría de las veces), asociamos a la carga de prueba q toda la energía potencial del sistema.
El potencial eléctrico (magnitud escalar) y el campo eléctrico (magnitud vectorial) son propiedades de cada punto, existiendo independientemente de que en él esté colocada una carga o no.
El vector campo eléctrico E y el potencial eléctrico V son dos maneras de describir el campo eléctrico existente en una región del espacio. Algunas veces es más conveniente Usar el vector E y, en otras, el potencial V.

⚡ Potencial Eléctrico en un punto de una Carga

Considere el campo eléctrico generado por una partícula electrizada con carga Q. Vamos a colocar una carga de prueba q en un punto P de ese campo, a una distancia d de Q.

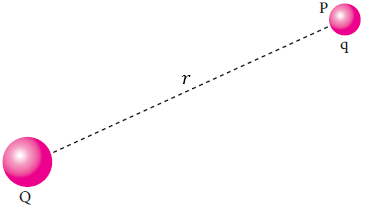
Potencial Eléctrico creado por una partícula puntual

La energía potencial eléctrica almacenada en el sistema constituido por las dos cargas es dada por:

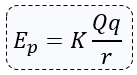
Fórmula de energía potencial eléctrica

En dónde K es la constante electrostática del medio.

La demostración de esa expresión requiere conocimiento de cálculo diferencial e integral. Sin embargo, podemos utilizar una forma simplificada para esta demostración. Si se piensa que la carga Q se encuentra fija, la carga de prueba q, al desplazarse hasta el punto P, estará sujeta a una fuerza eléctrica de intensidad variable F, desplazándose una distancia r. Considerando el valor medio de la intensidad de la fuerza (F) como constante (Fm), el trabajo realizado por ella es responsable de la energía potencial adquirida por el sistema.

Es decir:

$\displaystyle {{E}_{p}}=W={{F}_{m}}\cdot d\cdot \cos \theta$

Como la carga q se moverá en dirección del mismo sentido de la fuerza eléctrica, entonces tenemos que no hay ángulo, por lo tanto θ = 0° , y nuestra fórmula quedaría así:

$\displaystyle {{E}_{p}}={{F}_{m}}\cdot d\cdot (1)={{F}_{m}}\cdot d$

La fuerza no es mas que la Ley de Coulomb, entonces sustituyendo en la fuerza, obtenemos:

$\displaystyle {{E}_{p}}={{F}_{m}}\cdot d=K\frac{Qq}{{{r}^{2}}}\cdot d=K\frac{Qq}{r}$

Si sabemos que la energía potencial, la podemos escribir como:

$\displaystyle {{E}_{p}}=qV$

Igualando con la fórmula anterior de energía potencial eléctrica

$\displaystyle qV=K\frac{Qq}{r}$

$\displaystyle V=K\frac{Qq}{qr}=K\frac{Q}{r}$

$\displaystyle V=K\frac{Q}{r}$

Es decir:

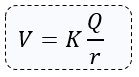
Fórmula de potencial eléctrico

El gráfico representativo del potencial en función de la distancia a la carga puntiforme generadora del campo eléctrico es una curva denominada hipérbola equilátera.

Gráfica de una hipérbola equilátera

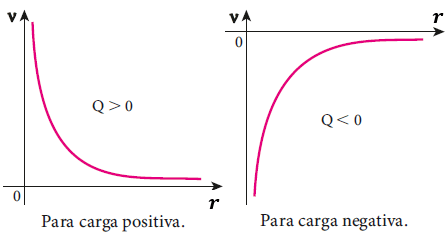
Observando los gráficos, se percibe que el potencial tiende a cero, cuando la distancia tiende al infinito. Esto ocurre tanto para la carga positiva y para la negativa. por lo tanto:

El nivel cero del potencial creado por una carga puntiforme está, generalmente, en el "infinito".

Debemos entender por "infinito" un lugar suficientemente alejado de la carga Q, de modo que sus influencias en otras cargas sean despreciables.

🔋 Potencial Eléctrico Creado por Varias Cargas Puntuales

Suponga un lugar del espacio donde se encuentran n partículas electrizadas. Consideremos, ahora, un punto A, sujeto a los n campos eléctricos creados por las cargas. Una vez que el potencial eléctrico es una magnitud escalar, tendremos, en el punto A, un potencial resultante de valor igual a la suma algebraica de los n potencial creados individualmente por las cargas.

Así, sería la expresión:

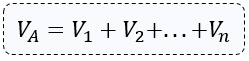
Potencial eléctrico de varias partículas

🔮 Superficies Equipotenciales

Las Superficies Equipotenciales son líneas (en el plano) o superficies (en el espacio) en las que el potencial, en todos los puntos, asume el mismo valor algebraico.

Las equipotenciales, en un campo eléctrico creado por una partícula electrizada y solitaria, son circunferencias (en el plano) o superficies esféricas (en el espacio). Tal afirmación es fácilmente constatable, bastando para ello analizar la expresión del potencial. Obsérvese que, para los mismos Q y K, el potencial asumirá valores iguales en los puntos del espacio equidistantes de la carga fuente:

$\displaystyle V=K\frac{Q}{r}$

Teniendo K y Q valores fijos, para distancias r iguales tenemos el mismo potencial V.

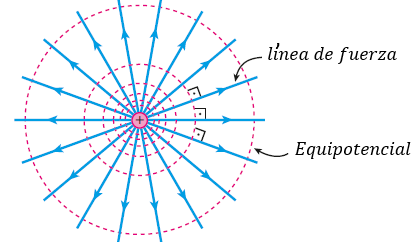
Superficies Equipotenciales

En la ilustración, vemos la representación de equipotenciales en un campo eléctrico creado por una carga puntual positiva. Observe que, si la carga fuera negativa, cambiaría sólo el sentido de las líneas de fuerza, que pasarían a ser de aproximación. Con respecto a las equipotenciales, nada se alteraría. En el espacio, en lugar de circunferencias concéntricas, tendríamos superficies esféricas concéntricas.

En un dipolo eléctrico, es decir, en el caso de dos partículas electrizadas con cargas del mismo módulo, pero de señales opuestas, las equipotenciales asumen el aspecto de la figura a seguir.

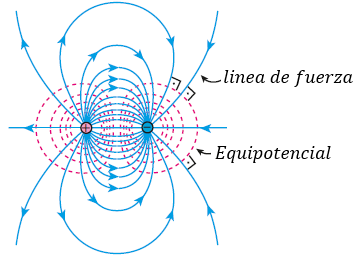
Dipolo Equinopotencial

Las equipotenciales (líneas o superficies) son perpendiculares a las líneas de fuerza.

Como ya vimos, el vector campo eléctrico E es siempre tangente a la línea de fuerza, con sentido coincidente con la orientación de la línea. Así, cuando tenemos una superficie equipotencial, tanto la línea de fuerza como el vector campo eléctrico son perpendiculares a ella, en todos sus puntos, como ilustra la figura abajo.

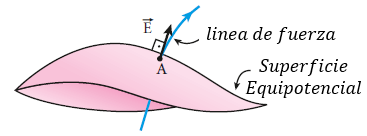
superficie equipotencial

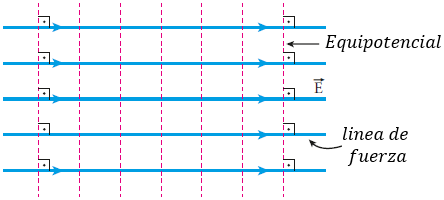
En un campo eléctrico uniforme, las equipotenciales son rectas (en el plano) o superficies planas (en el espacio), también perpendiculares a las líneas de fuerza, como representa la figura

superficies planas equipotenciales

⭕ Diferencia de Potencial Eléctrico

Por lo general no es tan importante o relevante conocer el potencial eléctrico que existe en un determinado punto, sino más bien saber cual es la diferencia de potencial entre dos puntos y con ello calcular la cantidad de trabajo necesario para mover cargas eléctricas de un punto a otro.

La Diferencia de Potencial entre dos puntos cualesquiera A y B, es igual al trabajo por unidad de carga positiva que realizan las fuerzas eléctricas al mover una carga de prueba desde el punto A al B.

Se tiene por fórmula matemática lo siguiente:

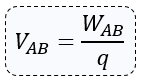
Fórmula de la diferencia de potencial

Dónde:

Vab = Diferencia de potencial entre los puntos A y B (expresada en Volts)

Wab = Trabajo realizado sobre una carga de prueba q que se desplaza de A a B (expresada en Joules)

q = Carga de prueba desplazada de A a B (expresada en Coulombs)

A menudo la diferencia de potencial se le llama por otros nombres, como por ejemplo: voltaje o tensión. Al igual que el potencial eléctrico, la diferencia de potencial es una magnitud escalar.

La diferencia de potencial se puede obtener muy fácil si se conoce el potencial de cada uno, de esta forma:

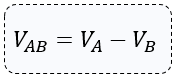
fórmula de la diferencia de potencial

Si se quisiera saber cuál es el trabajo realizado por el campo eléctrico al mover una carga q desde un punto A al punto B, de la primera ecuación de diferencia de potencial eléctrico despejamos a Wab y nos queda:

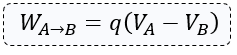
Fórmula para mover una carga

🔸 Ejercicios Resueltos de Potencial Eléctrico

Problema 1.- Determine la carga transportada desde un punto a otro punto al realizarse un trabajo de 5x10¯³ Joules, si la diferencia de potencial es de 2x10² Volts

Solución:

Este es un problema básico y muy sencillo sobre el potencial eléctrico, pues entre los datos nos proporciona el trabajo a realizarse, así como la diferencia de potencial entre los dos puntos, por lo tanto solamente tenemos que aplicar la fórmula de potencial eléctrico y despejar a la variable de la carga "q".

Datos:

$\displaystyle W=5x{{10}^{-3}}J$

$\displaystyle V=2x{{10}^{2}}V$

a) Obteniendo el valor de la carga

De la fórmula de potencial eléctrico

$\displaystyle V=\frac{W}{q}$

Despejando a "q" de la fórmula.

$\displaystyle q=\frac{W}{V}$

Sustituyendo los valores en la fórmula despejada:

$\displaystyle q=\frac{W}{V}=\frac{5x{{10}^{-3}}J}{2x{{10}^{2}}V}=2.5x{{10}^{-5}}C$

Obtenemos un valor de 2.5x10^(-5) Coulombs

Problema 2.- Una carga de 7μC se colca en un determinado punto de un campo eléctrico y adquiere una energía potencial de 5x10^(-5) Joules ¿Cuál es el potencial eléctrico en ese punto?

Solución:

En este problema no nos proporciona ningún dato del trabajo de mover la carga, pero si nos dan una energía potencial que en términos generales es también unidad de trabajo, adicionalmente nos dan el valor de la carga. Así que para obtener el valor del potencial eléctrico, tendremos que hacerlo de la siguiente manera.

Datos:

$\displaystyle {{E}_{p}}=5x{{10}^{-5}}J$

$\displaystyle q=7\mu C=7x{{10}^{-6}}C$

a) Obteniendo el valor del potencial eléctrico

Para este caso, utilizaremos la siguiente fórmula:

$\displaystyle V=\frac{{{E}_{p}}}{q}$

Sustituyendo nuestros datos en la fórmula:

$\displaystyle V=\frac{{{E}_{p}}}{q}=\frac{5x{{10}^{-5}}J}{7x{{10}^{-6}}C}=7.14V$

Obteniendo así un valor de 7.14 Volts como diferencia de potencial.

Problema 3.- Determinar el potencial eléctrico a una distancia de 17 cm de una carga puntual de 8 nC

Solución:

Cuando haya problemas de potencial eléctrico donde nos proporcionen distancias, es porque estamos hablando de la fórmula de potencial eléctrico en un punto, por lo que la fórmula será distinta a la de los ejercicios anteriores, por lo que partiendo de esto, podemos reunir los datos y comenzar a resolver.

Datos:

$\displaystyle q=8nC=8x{{10}^{-9}}C$

$\displaystyle r=17cm\left( \frac{1m}{100cm} \right)=0.17m$

$\displaystyle K=9x{{10}^{9}}\frac{N{{m}^{2}}}{{{C}^{2}}}$

a) Obteniendo el potencial eléctrico

Para este tipo de casos, aplicaremos la siguiente fórmula:

$\displaystyle V=\frac{Kq}{r}$

Sustituyendo nuestros datos en la fórmula, obtenemos:

$\displaystyle V=\frac{Kq}{r}=\frac{\left( 9x{{10}^{9}}\frac{N{{m}^{2}}}{{{C}^{2}}} \right)\left( 8x{{10}^{-9}}C \right)}{0.17m}=423.52V$

Obtenemos un potencial eléctrico de 423.52 Volts

Problema 4.- Una carga de prueba se mueve del punto A al B como se en la figura. Calcular: a) La diferencia de potencial Vab, si la distancia del punto A a la carga Q de 5μC es de 35 cm y la distancia al punto B a la carga Q es de 50cm. b) El trabajo realizado por el campo eléctrico de la carga Q al mover la carga de prueba de 11nC desde el punto A al punto B

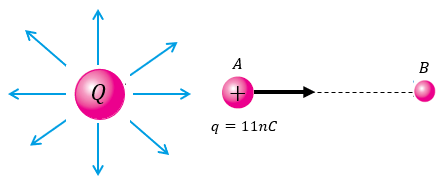
problema_de_potencial_electrico

Solución:

Este problema es mucho más complejo que los tres anteriores, por lo tanto requiere más análisis y observación. Si volvemos a leer el problema y observamos la imagen vamos a entender que los cálculos serán a través de la fórmula que aplicamos en el problema 3.

Datos:

$\displaystyle Q=5\mu C=5x{{10}^{-6}}C$

$\displaystyle {{r}_{A}}=35cm\left( \frac{1m}{100cm} \right)=0.35m$

$\displaystyle {{r}_{B}}=50cm\left( \frac{1m}{100cm} \right)=0.5m$

$\displaystyle K=9x{{10}^{9}}\frac{N{{m}^{2}}}{{{C}^{2}}}$

$\displaystyle q=11nC=11x{{10}^{-9}}C$

a) Obtener la diferencia potencial de Vab

Debemos entender para poder calcular la diferencia de potencial entre los puntos A y el punto B, primero debemos calcularlos individualmente, así que comencemos con el punto A

$\displaystyle {{V}_{A}}=\frac{KQ}{{{r}_{A}}}$

➡ Sustituyendo los datos para el caso de A:

$\displaystyle {{V}_{A}}=\frac{KQ}{{{r}_{A}}}=\frac{\left( 9x{{10}^{9}}\frac{N{{m}^{2}}}{{{C}^{2}}} \right)\left( 5x{{10}^{-6}}C \right)}{0.35m}=128.57x{{10}^{3}}V$

Obteniendo así un valor de 128.57x10^3 Volts

➡ Sustituyendo los datos para el caso de B:

$\displaystyle {{V}_{B}}=\frac{KQ}{{{r}_{B}}}=\frac{\left( 9x{{10}^{9}}\frac{N{{m}^{2}}}{{{C}^{2}}} \right)\left( 5x{{10}^{-6}}C \right)}{0.5m}=90x{{10}^{3}}V$

Obteniendo así un valor de 90x10^3 Volts

Por lo tanto la diferencia de potencial de Vab, sería:

$\displaystyle {{V}_{AB}}={{V}_{A}}-{{V}_{B}}$

$\displaystyle {{V}_{AB}}=128.57x{{10}^{3}}V-90x{{10}^{3}}V=38.57x{{10}^{3}}V$

Un valor de 38.57x10^3 Volts

b) Obtener el trabajo realizado por el campo eléctrico

Para poder obtener el valor del trabajo del campo eléctrico de la carga Q para mover del punto A al punto B a la carga de prueba, es importante aplicar la siguiente fórmula:

$\displaystyle {{W}_{A\to B}}=q\left( {{V}_{A}}-{{V}_{B}} \right)$

Recordar que el valor de Q y q no son los mismos, el valor de q es el valor de la carga de prueba.

Sustituyendo nuestros datos en la fórmula:

$\displaystyle {{W}_{A\to B}}=q\left( {{V}_{A}}-{{V}_{B}} \right)=11x{{10}^{-9}}C\left( 38.57x{{10}^{3}}C \right)=4.24x{{10}^{-4}}J$

Por lo que el valor del trabajo del campo eléctrico fue de 4.24x10^(-4) Joules

Problema 5.- Una carga de 7μC está separada por 45 cm de otra carga de 4μC. ¿Cuál es la energía potencial del sistema?

Solución:

Este problema es muy diferente a los cuatro anteriores, sin embargo tiene un parecido al problema 2. El problema nos proporciona dos cargas y una distancia entre ambas. Y nos pide la energía potencial que existe entre las cargas. Vamos a recoger los datos y a resolver.

Datos:

$\displaystyle Q=7\mu C=7x{{10}^{-6}}C$

$\displaystyle q=4\mu C=4x{{10}^{-6}}C$

$\displaystyle r=45cm\left( \frac{1m}{100cm} \right)=0.45m$

$\displaystyle K=9x{{10}^{9}}\frac{N{{m}^{2}}}{{{C}^{2}}}$

a) Obtener la energía potencial del sistema

Para obtener la energía potencial del sistema, aplicamos la siguiente fórmula:

$\displaystyle {{E}_{p}}=\frac{kQq}{r}$

Sustituyendo nuestros datos en la fórmula:

$\displaystyle {{E}_{p}}=\frac{kQq}{d}=\frac{\left( 9x{{10}^{9}}\frac{N{{m}^{2}}}{{{C}^{2}}} \right)\left( 7x{{10}^{-6}}C \right)\left( 4x{{10}^{-6}}C \right)}{0.45m}=0.56J$

Por lo que la energía potencial del sistema es de 0.56 Joules.

Carlos julián

Carlos Julián es Ingeniero Mecatrónico, profesor de Física y Matemáticas.

Temas que podrían interesarte 👇

46 Comentarios Publicados

Zusi Rose Bud dice:

5 mayo, 2020 a las 1:10 pm

Determine la carga transportada desde un punto a otro
punto al realizarse un trabajo de 8×10 ̄3 Joules, si la
diferencia de potencial es de 9×102 Volts

Responder
1. Elias dice:
  
  3 noviembre, 2021 a las 2:40 pm
  
  Usando la formula de trabajo que es igual a: T=Q(Va-Vb), despejando nos quedaría: Q=T/Va-Vb, con esto se sustituye y debe dar el valor de la carga en Couloms
  
  Responder
  1. Ligia dice:
    
    12 febrero, 2022 a las 7:23 am
    
    Una carga eléctrica está en un campo eléctrico uniforme de 25new/cb cuando se desplaza 4cm realiza 7cm trabajo de 5 joules. Calcular la diferencia de potencial y cuál es el valor de la carga ?
    
    Responder
Zusi Rose Bud dice:

5 mayo, 2020 a las 1:11 pm

Determinar el potencial eléctrico a una distancia de 15 cm
de una carga puntual de 5x10^-6 C
Ayuda plis...

Responder
1. Elias dice:
  
  3 noviembre, 2021 a las 2:45 pm
  
  Con la formula de potencial electrico que dice: V=Kq/r, donde K es una constante del vacio que equivale a 9x10^9 Nm^2/C^2 y q es la carga que te dan entre r que equivale a la distancia. el resultado debe darte en Volts (v)
  
  Responder
2. Maya Anjhy dice:
  
  28 junio, 2023 a las 9:51 pm
  
  La respuesta es 299.700 voltios
  
  Responder
LORENZO ALFREDO ENRIQUEZ GARCIA dice:

24 mayo, 2020 a las 11:37 am

Muy buena informacion. Gracias

Responder
1. Arnol Camilo paz dice:
  
  18 octubre, 2021 a las 12:20 pm
  
  . Calculeeltrabajorealizadoenlatransferenciadeunacargade5CdelpuntoA(1,2,−4)alpuntoB(3,−5,6) en un campoel´ectrico E = ax +z2ay +2yzaz V/m. Cómo podría desarrollar ese tipo de ejercicio?
  
  Responder
nano rios dice:

18 junio, 2020 a las 11:42 pm

la teoría de este tema es relativamente compleja ,pero aca nos la facilitan y ademas los ejercicios planteamos de forma didáctica y sencilla , ayuda a perder el miedo ...

Responder
Daniel RM dice:

3 septiembre, 2020 a las 7:51 pm

Muy buenos ejercicios. Muchas gracias

Responder
Sergio A. Solorzano dice:

29 septiembre, 2020 a las 12:08 pm

Muy buenos artículos tanto para maestros como para alumnos de Física.

Responder
1. Carlos julián dice:
  
  1 abril, 2021 a las 10:22 am
  
  Gracias Sergio!
  
  Responder
José Vargas dice:

22 noviembre, 2020 a las 6:15 am

Muy bueno el articulo...pueden ayudarme con este ejercicio? se tiene dos laminas metalicas paralelas colocadas una frente a la otra de area 500 cm2 con carga de 3.2x10-8C . calcular ....... a) la magnitud del campo electrico entre las placas b)la aceleracion con la cual se desplaza un electron que partio desde el reposo c)la separacion de las laminas si el electro tarda 1.2x10-8s en ir de una lamina hasta la otra.. Procedimientos.

Responder
wilmer dice:

20 enero, 2021 a las 8:57 am

excelente me gusta esta pagina

Responder
1. Carlos julián dice:
  
  1 febrero, 2021 a las 6:54 pm
  
  Gracias Wilmer!! Ayúdanos a compartir los ejercicios con tus amigos!
  
  Responder
ª dice:

1 febrero, 2021 a las 9:05 pm

Tres cargas eléctricas están ubicada en los vértices de un triangulo como lo
muestra la figura. Hallar: a) el potencial eléctrico en el punto P, b) Energia
potencial eléctrica que adquiere una carga q= 2,5 μC, ubicada en el punto P.
Q1= 5μC, Q2= -2μC, Q3= 5μC.
Cuál sería el resultado?

Responder
1. Elias dice:
  
  3 noviembre, 2021 a las 3:15 pm
  
  no se puede realizar debido a que no mostraste la figura
  
  Responder
Rosalia dice:

5 febrero, 2021 a las 7:00 am

Gracias por la informacion , bien explicada y con sus formulas , yo le añadiria un dibujo a cada ejercicio pero esta genial.

Responder
1. Carlos julián dice:
  
  22 marzo, 2021 a las 8:55 am
  
  Gracias por tu comentario Rosalia, lo vamos a implementar!
  
  Responder
fabiana dice:

6 febrero, 2021 a las 7:25 pm

un electrón se mueve entre dos puntos de un campo electrico uniforme cuya diferencia de potencial es 10000 voltios. calcular el trabajo realizado para moverse. alguien que me ayude

Responder
camila veliz dice:

16 febrero, 2021 a las 11:15 am

excelente trabajo

Responder
1. Carlos julián dice:
  
  16 febrero, 2021 a las 12:12 pm
  
  Muchas gracias Camila!
  
  Responder
  1. Daniel Ortiz dice:
    
    8 diciembre, 2021 a las 3:43 pm
    
    Tres cargas de magnitud:14 nC, -6 nC y 8 nC se encuentran separadas por 4m cada una. Dibuje el vector fuerza.
    Determine las componentes de la fuerza eléctrica en la a carga de 14 nC.
    Si la carga de 8n C es negativa, dibuje el vector fuerza eléctrica.
    
    Responder
2. Willy dice:
  
  17 marzo, 2021 a las 1:54 pm
  
  Nesecito una ayuda para resolver un ejercicio
  
  Responder
jorge dice:

22 febrero, 2021 a las 11:25 am

Que cantidad de trabajo se requiere para mover una carga de 3,6 uc 3,6 por 10 a la menos 6 aplicando un ddp de 95000 v

Responder
Willy dice:

17 marzo, 2021 a las 1:58 pm

Este es él ejercicio que potencial electronico existe en un campo electronico si este tuvo que efectuar un trabajo de A.0,17 joule para trasladar una carga de A. 17 UC A17 micro coulomb desde ese punto hasta él infinito

Responder
Victorino Ortega dice:

19 marzo, 2021 a las 8:46 pm

Buenas noches:
Imparto las materias de matemáticas y Física a nivel medio superior.
La página regularmente la uso para mis clases tanto presenciales como en videoconferencias, y
es de gran ayuda para desarrollar mis trabajos académicos.
Sin mas por el momento, le agradezco su amable atención.
Profesor: Victorino Ortega

Responder
1. Carlos julián dice:
  
  22 marzo, 2021 a las 8:27 am
  
  Nos da mucho gusto Victorino, saludos!
  
  Responder
vicente dice:

1 octubre, 2021 a las 4:44 pm

Una carga de 5μC está separada por 50 cm de otra carga de 4mC. ¿Cuál es la diferencia de potencial del sistema?

Responder
José Rodríguez dice:

7 noviembre, 2021 a las 11:01 am

Aqui tengo un ejercicio, que solicito ayuda para resolver:
En un medio de Er = 4 se coloca una carga de valor 56.10-5 C a una distancia de 28 cm de un punto A. Calculo el potencial eléctrico que genera esta carga.

Responder
1. Yurbis lira dice:
  
  16 febrero, 2022 a las 6:18 am
  
  Prox necesito ayuda para este ejercicio
  Una carga de 7uC separada por 4cm ¿cual es la energía potencial del sistema ?
  
  Responder
José Rodríguez dice:

7 noviembre, 2021 a las 11:02 am

Qué pasa cuando la carga no está en el vacio?

Responder
1. Carlos julián dice:
  
  8 noviembre, 2021 a las 10:09 am
  
  Se tiene que calcular esa permeabilidad
  
  Responder
PepitoAlcachofa dice:

13 febrero, 2022 a las 4:32 pm

me pueden ayudar con este ejercicio porfavor urgente - Se tiene un condensador plano, el cual está constituido por armaduras de 0,5 m2
cada una y separadas entre sí 101,72.10-5
cm. Si el dieléctrico interpuesto entre las armaduras tiene un valor de 4,6, calcular la capacidad del condensador en
microfaradio. R. C = 2 μF.
y este Cuando se carga un condensador se realizo un trabajo de 8x10ala-4 Joules. Calcular el valor de la carga electrica si su capacidad es de 4x10ala-12 microfaladio.

Responder
Yurbis lira dice:

16 febrero, 2022 a las 6:16 am

Prox necesito ayuda para este ejercicio
Una carga de 7uC separada por 4cm cual es la energía potencial del sistema

Responder
Yurbis lira dice:

16 febrero, 2022 a las 6:24 am

Profesor buen día necesito su ayuda para este ejercicio .
Una carga de 7uC separada por 4cm ¿cual es la energía potencial del sistema ?

Responder
Enrique dice:

22 mayo, 2022 a las 4:21 pm

Profesor en el ejercicio número tres cuál magnitud es grande o mayor
Q o q.?

Responder
Enrique dice:

22 mayo, 2022 a las 4:22 pm

Perdón profesor es en el problema 4

Responder
Evelyn dice:

10 junio, 2022 a las 1:47 am

datos formula
r=15cm=0.15m V=Kq/r
q=5x10^-6c
k=9.0x10^9Nm2/c2 desarrollo
V=(9.0x10^9NM2/C2)(5x10^-6C)/0.15
V=6,750NM/C=J/C=Volts

Responder
Rosa dice:

17 junio, 2022 a las 1:06 pm

Se tiene una esfera cuyo radio es de 3 m determinar su carga sabiendo que su potencial es de 60 stv

Responder
Rafael dice:

20 octubre, 2022 a las 11:57 pm

Este es un buen blog que recomendaré a todos mis compis de clase. Me ha ayudado mucho, gracias

Responder
Rafael dice:

22 octubre, 2022 a las 12:38 am

Dos cargas electricas, Q1 y Q2, se encuentran situadas en el vacío a una distancia de 2m. Si la intensidad del campo eléctrico en el punto medio entre ambas cargas es nulo y el potencial en dicho punto es de 3.6×10^4 V, calculs el valor de las cargas Q1 y Q2.

Responder
Yoviver dice:

21 noviembre, 2022 a las 9:07 am

Pueden subir mas ejercicios, porfa

Responder
1. Carlos julián dice:
  
  21 noviembre, 2022 a las 10:40 am
  
  Estamos trabajando en ello, ayúdanos a compartir.
  
  Responder
  1. mary dice:
    
    6 abril, 2023 a las 2:56 pm
    
    podrian subir mas ejercicios de V=Ep/d
    
    Responder
[email protected] dice:

17 mayo, 2024 a las 4:43 pm

Me gustaría aprender ya que estoy estudiando

Responder

Deja una respuesta Cancelar la respuesta