Principio de Superposición - Ejercicios Resueltos

Después de entender los conceptos básicos de la Ley de Coulumb es importante tener en cuenta que las fuerzas entre cargas eléctricas no solamente se calculan mediante dos cargas, sino que también podemos hacer cálculos para más de dos cargas y a ese método se le conoce como principio de superposición 😮

Éste principio de superposición se basa de la siguiente manera. ¡Presta atención! , si tenemos tres cargas las llamaremos q1, q2 y q3 respectivamente , si queremos saber cuál es la fuerza ejercida por las cargas q2 y q3 sobre la q1 , primero se debe encontrar la fuerza ejercida de q2 sobre q1 y después la q3 sobre la q1, una vez teniendo este paso realizado, se deben sumar las fuerzas vectorialmente para obtener la fuerza resultante sobre q1. ¿se entiende?

Si no se entiende, no hay problema... Lo veamos con un claro ejemplo.

Problemas Resueltos de Superposición de Cargas

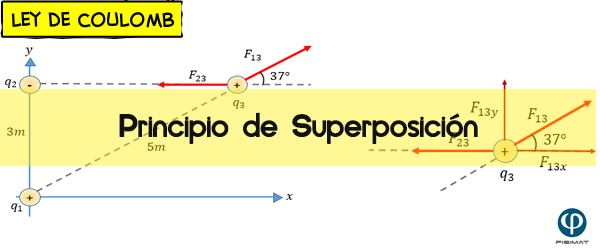
Problema 1

Nota: La fuerza ejercida por q1 sobre q3 es $\displaystyle {{F}_{13}}$ , la fuerza ejercida por q2 sobre q3 es $\displaystyle {{F}_{23}}$ , ahora la fuerza resultante ejercida sobre q3 es el  vector $\displaystyle {{F}_{13}}+{{F}_{23}}$

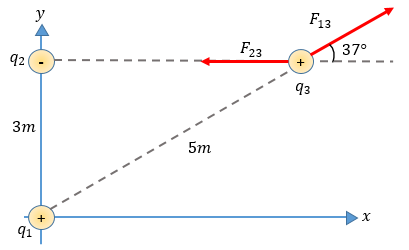
Análisis: Es importante darse cuenta de lo que el problema pide, nos está advirtiendo encontrar la dirección de las fuerzas que ejercen en q1 y q2 sobre q3 , pero también debemos ser observadores y darnos cuenta que la fuerza de atracción entre q2 y q3 es de atracción pues ambas cargas son de signos contrarios, y lógicamente la fuerza de atracción entre q1 y q3 es de repulsión porque ambas cargas son positivas.

Ahora pasemos a calcular las fuerzas de atracción o repulsión respectivamente.  😎

Solución: Calculemos la magnitud de la fuerza ejercida de q2 sobre q3.

$\displaystyle {{F}_{23}}=K\frac{{{q}_{2}}\cdot {{q}_{3}}}{{{r}^{2}}}=(9x{{10}^{9}}\frac{N\cdot {{m}^{2}}}{{{C}^{2}}})\frac{(2x{{10}^{-9}}C)(5x{{10}^{-9}}C)}{{{(4m)}^{2}}}=5.63x{{10}^{-9}}N$

Ahora calculemos la magnitud de la fuerza ejercida de q1 sobre q3, y esto sería:

$\displaystyle {{F}_{13}}=K\frac{{{q}_{1}}\cdot {{q}_{3}}}{{{r}^{2}}}=(9x{{10}^{9}}\frac{N\cdot {{m}^{2}}}{{{C}^{2}}})\frac{(6x{{10}^{-9}}C)(5x{{10}^{-9}}C)}{{{(5m)}^{2}}}=1.08x{{10}^{-8}}N$

Ahora tenemos que ser muy cuidadosos en el siguiente análisis después de haber calculado las fuerzas, ya que si vemos la imagen del problema, la fuerza ejercida por q1 sobre q3 forma un ángulo de 37 grados respecto al eje "x", y este dato nos va a servir para poder calcular la suma vectorial, es decir la fuerza resultante que actúa sobre q3.

Obteniendo la fuerza resultante sobre q3

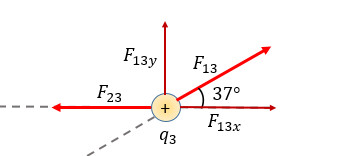
Nos vamos a centrar en q3, que es donde tenemos que calcular la resultante, si observamos la imagen , nos damos cuenta que hemos colocado $\displaystyle {{F}_{13x}}$ y ya que ese vector al tener un ángulo de inclinación tenemos que descomponerlo en sus componentes rectangulares y hacer la suma vectorial.

Pasemos entonces a descomponer ese vector, primero en "x" y después en "y".

$\displaystyle {{F}_{13x}}={{F}_{13}}\cdot \cos 37{}^\circ =1.08x{{10}^{-8}}\cdot \cos 37{}^\circ =8.63x{{10}^{-9}}N$

$\displaystyle {{F}_{13y}}={{F}_{13}}\cdot sen37{}^\circ =1.08x{{10}^{-8}}\cdot sen37{}^\circ =6.5x{{10}^{-9}}N$

Ahora es momento de realizar la suma vectorial, recordar que en la suma vectorial es importante saber que lo que está a la derecha es positivo, y lo que está a la izquierda es negativa según el marco de referencia.

Haciendo la suma:

$\displaystyle {{f}_{x}}=8x63x{{10}^{-9}}N-5.63x{{10}^{-9}}N=3.01x{{10}^{-9}}N$

$\displaystyle {{f}_{y}}=6.5x{{10}^{-9}}N$

En el eje"y" no tenemos más fuerzas, más que la fuerza que ejerció q2 sobre q3, pero como vimos fue una fuerza de atracción y es por eso que la reacción fue hacía el lado izquierdo.

Ahora procedemos a calcular la fuerza resultante, mediante el teorema de pitágoras.

$\displaystyle {{F}_{R3}}=\sqrt{{{(3.01x{{10}^{-9}}N)}^{2}}+{{(6.5x{{10}^{-9}}N)}^{2}}}=7.16x{{10}^{-9}}N$

y procedemos también a calcular la dirección del vector resultante.

$\displaystyle \theta ={{\tan }^{-1}}\left( \frac{{{f}_{y}}}{{{f}_{x}}} \right)={{\tan }^{-1}}\left( \frac{6.5x{{10}^{-9}}N}{3.01x{{10}^{-9}}N} \right)=65.2{}^\circ $

Con todo éste cálculo tendríamos ya la respuesta correcta.

En el siguiente ejemplo veremos un problema un poco diferente al primero, pero aplicando la misma fórmula de Coulomb y el método de superposición.

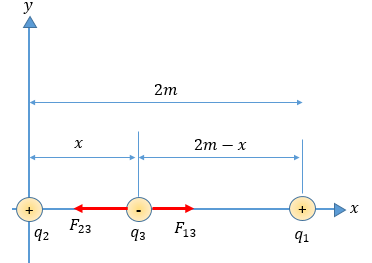
Análisis:  El problema es sencillo realmente, solo que debemos pensar a profundidad que ocurre. Así que si prestas atención podremos seguir el hilo del ejercicio sin detalles y dudas. Si nos damos cuenta la fuerza resultante debe ser cero según el problema, pero para que eso suceda la fuerza de atracción que hay de q2 sobre q3 y de q1 sobre q3 deben ser iguales, ya que al sumarlas nos darán cero. 😎

$\displaystyle {{F}_{13}}={{F}_{23}}$

Solución: Tomemos en cuenta las coordenadas que se observan en la imagen para poder aplicar la ley de Coulomb, por ahora no nos interesa el valor de la carga de q3 , y eso lo vamos a ver en breve.

Formulando tenemos que:

$\displaystyle {{F}_{13}}=K\frac{(15x{{10}^{-6}}C)({{q}_{3}})}{{{(2-x)}^{2}}}$

$\displaystyle {{F}_{23}}=K\frac{(6x{{10}^{-6}}C)({{q}_{3}})}{{{x}^{2}}}$

Como deben ser iguales entonces colocamos lo siguiente:

$\displaystyle K\frac{(15x{{10}^{-6}}C)({{q}_{3}})}{{{(2-x)}^{2}}}=K\frac{(6x{{10}^{-6}}C)({{q}_{3}})}{{{x}^{2}}}$

Lo que se parezca del primer miembro con lo del segundo miembro, pueden eliminarse sin ningún problema, puesto que al despejar una variable sobre el otro lado éstas se cancelan, ¿no sabes por qué? entonces te recomiendo leer el artículo de ¿Cómo despejar fórmulas?

Bien, aclarado este punto entonces tenemos que:

$\displaystyle \frac{(15x{{10}^{-6}}C)}{{{(2-x)}^{2}}}=\frac{(6x{{10}^{-6}}C)}{{{x}^{2}}}$

Eliminamos el valor de la carga q3 que no sabíamos pero es una variable, así como la constante K y el x10 elevado a la menos 6.

Ahora podemos hacer el despeje correcto y tendremos lo siguiente:

$\displaystyle {{x}^{2}}(15)={{(2-x)}^{2}}(6)$

Si nos damos cuenta podemos sacar la raíz cuadrada de ambos miembros , con eso eliminamos los cuadrados, quedando así:

$\displaystyle \sqrt{{{x}^{2}}(15)}=\sqrt{{{(2-x)}^{2}}(6)}$

Un poco de álgebra y tenemos

$\displaystyle x\sqrt{15}=(2-x)\sqrt{6}$

Invirtiendo la igualdad y despejando a la raíz de 6, nos queda

$\displaystyle \frac{x\sqrt{15}}{\sqrt{6}}=(2-x)$

$\displaystyle 1.58x=2-x$

Pasando a sumar a "x" y factorizando

$\displaystyle 1.58x+x=2$

$\displaystyle x(1.58+1)=2$

$\displaystyle x(2.58)=2$

"despejando a x"

$\displaystyle x=\frac{2}{2.58}=0.78$

Por lo que podemos decir que a la distancia para colocar a la carga de q3 es de 0.78 m,