Problema 2 de Dilatación Superficial

De forma similar al ejemplo anterior, en este problema de Dilatación Superficial reforzamos el concepto principal que es la utilización correcta de la fórmula, con ello se proporciona la solución paso a paso del ejemplo y nuevamente el alumno comprueba sus resultados de manera correcta y concisa. 😊👇

Nivel de Dificultad: ⭐⭐

Solución:

A diferencia del ejercicio anterior podemos observar que aquí la temperatura no aumenta, sino que el problema nos dice que la temperatura disminuye a 9°C es lógico que al disminuir la temperatura el cuerpo que se dilata tendrá que disminuir y no aumentar. ¿será cierto?, veamos entonces la solución.

• Obtener el área final del portón de hierro

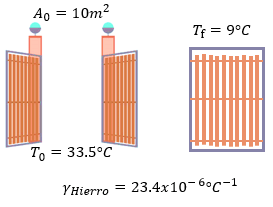
Datos:

$\displaystyle {{\gamma }_{Hierro}}=23.4x{{10}^{-6}}^{{}^\circ }{{C}^{-1}}$

$\displaystyle {{A}_{0}}=10{{m}^{2}}$

$\displaystyle {{T}_{0}}=33.5{}^\circ C$

$\displaystyle {{T}_{f}}=9{}^\circ C$

a) Obteniendo el área final

Veamos la fórmula del área final

Sustituyendo nuestros datos en la fórmula:

$\displaystyle {{A}_{f}}=10{{m}^{2}}[1+23.4x{{10}^{-6}}^{{}^\circ }{{C}^{-1}}\left( {{9}^{{}^\circ }}C-{{33.5}^{{}^\circ }}C \right)]$

Realizando la diferencia de temperaturas ΔT

$\displaystyle {{A}_{f}}=10{{m}^{2}}[1+23.4x{{10}^{-6}}^{{}^\circ }{{C}^{-1}}\left( -{{24.5}^{{}^\circ }}C \right)]$

Multiplicando lo que nos dio de diferencia por el coeficiente de dilatación superficial.

$\displaystyle {{A}_{f}}=10{{m}^{2}}\left( 1-0.0005733 \right)$

Realizando la resta

$ \displaystyle {{A}_{f}}=10{{m}^{2}}\left( 0.9994267 \right)$

Multiplicando por 10m²

$\displaystyle {{A}_{f}}=9.994267{{m}^{2}}$

Es decir que tenemos un área final de 9.994267 m²

Como resultado vemos que el área disminuyó en cuanto la temperatura disminuyó.

Resultado:

$ \displaystyle {{A}_{f}}=9.994267{{m}^{2}}$