Producto Vectorial - Ejercicios Resueltos
El producto vectorial o producto cruz, es una operación matemática entre dos vectores que como resultado obtenemos otro vector, dicho vector estará en ángulo recto con ambos vectores, es decir, que si tenemos un vector a y un vector b, tal como se aprecia en la siguiente imagen.
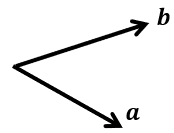
Y deseamos multiplicarlos usando el producto cruz o vectorial, tendríamos como resultado lo siguiente:
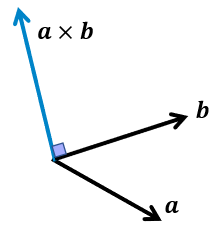
Todo esto ocurre en 3 dimensiones, pero no solo obtenemos un vector como resultante, sino también que el producto cruz o vectorial, nos da como resultado el área de un paralelogramo con lados a y b.
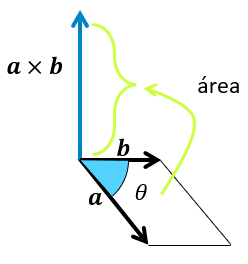
¿Cómo se calcula el Producto Cruz?
A diferencia del producto punto o producto escalar, el producto cruz o vectorial se calcula mediante la siguiente fórmula:
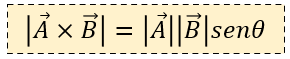
Dónde:
| A | = Es la magnitud o longitud del vector a
| B | = Es la magnitud o longitud del vector b
θ = es el ángulo entre el vector a y b
Si los vectores inician en el punto (0, 0, 0)
También podemos calcular el producto cruz con las componentes del vector están en el espacio, por ejemplo:
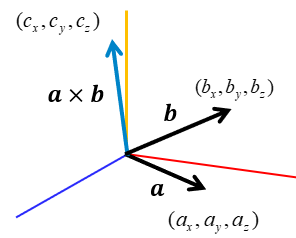
En este caso se formaría una matriz de la siguiente manera:
$\displaystyle \overrightarrow{A}\times \overrightarrow{B}=\left| {\begin{array}{*{20}{c}} {\widehat{i}} & {\widehat{j}} & {\widehat{k}} \\ {{{a}_{x}}} & {{{a}_{y}}} & {{{a}_{z}}} \\ {{{b}_{x}}} & {{{b}_{y}}} & {{{b}_{z}}} \end{array}} \right|$
Para obtener el resultado del producto cruz, de cada componente, se harían las siguientes operaciones
$\displaystyle {{c}_{x}}~=\text{ }{{a}_{y}}{{b}_{z}}~-\text{ }{{a}_{z}}{{b}_{y}}$
$\displaystyle {{c}_{y}}~=\text{ }{{a}_{z}}{{b}_{x}}~-\text{ }{{a}_{x}}{{b}_{z}}$
$\displaystyle {{c}_{z}}~=\text{ }{{a}_{x}}{{b}_{y}}~-\text{ }{{a}_{y}}{{b}_{x}}$
Más adelante veremos algunos ejercicios resueltos para entender mucho mejor el producto cruz o vectorial.
¿Cuál es la dirección?
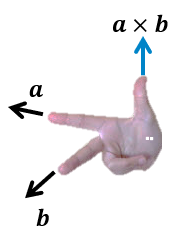
Si bien obtenemos un vector como resultante del producto cruz de dos vectores, la pregunta es ¿a qué dirección iría el vector resultante?, esto se puede calcular mediante la regla de la mano derecha, esta regla consiste apuntar con el dedo índice a lo largo del vector a y con el dedo medio a lo largo del vector b: el producto cruzado va en la dirección de nuestro pulgar.
Propiedades del Producto Vectorial
Ahora que sabemos la fórmula del producto cruz o vectorial, y que entendemos la regla de la mano derecha. Debemos de entender las propiedades que existen para poder aplicar este producto. Tal como lo muestra la siguiente tabla:
Ejercicios Resueltos del Producto Vectorial
Ahora es momento de realizar algunos ejercicios para aprender mucho mejor este tema.
Problema 1. Sea los vectores A y B que forman entre si un ángulo de 30°, y sabiendo que | a | = 6 y | b | = 5, calcular el producto cruz de ambos vectores
Solución:
Cuando se tienen las magnitudes de ambos vectores, es muy fácil poder calcular el producto cruz, ya que solamente debemos aplicar la fórmula:
$\displaystyle \left| {\overrightarrow{a}\times \overrightarrow{b}} \right|=\left| {\overrightarrow{a}} \right|\left| {\overrightarrow{b}} \right|sen\theta $
Sustituyendo nuestros datos:
$\displaystyle \left| {\overrightarrow{a}\times \overrightarrow{b}} \right|=\left| {\overrightarrow{a}} \right|\left| {\overrightarrow{b}} \right|sen\theta =(6)(5)sen30{}^\circ =30sen30{}^\circ =15$
Por lo que obtenemos como resultado 15
Problema 2. Un vector a tiene una magnitud 3, y un vector b tiene una magnitud de 4, y el ángulo entre a y b es de 60°
Solución:
Al igual que el ejemplo anterior, tendremos que multiplicar utilizando la fórmula:
$\displaystyle \left| {\overrightarrow{a}\times \overrightarrow{b}} \right|=\left| {\overrightarrow{a}} \right|\left| {\overrightarrow{b}} \right|sen\theta $
Sustituyendo nuestros datos:
$\displaystyle \left| {\overrightarrow{a}\times \overrightarrow{b}} \right|=\left| {\overrightarrow{a}} \right|\left| {\overrightarrow{b}} \right|sen\theta =(3)(4)sen60{}^\circ =12sen60{}^\circ =10.39$
Por lo que obtenemos un valor de 10.39
Problema 3. Cual es el producto cruz de a = (1, 2, 3) y b = (4, 5, 6)
Solución:
A diferencia de los dos ejemplos anteriores, no podemos hacer uso de la fórmula de manera directa, ya que los vectores tienen tres coordenadas que lo hacen estar en un espacio 3D, entonces aplicamos la siguiente fórmula:
$\displaystyle {{c}_{x}}~=\text{ }{{a}_{y}}{{b}_{z}}~-\text{ }{{a}_{z}}{{b}_{y}}$
$\displaystyle {{c}_{y}}~=\text{ }{{a}_{z}}{{b}_{x}}~-\text{ }{{a}_{x}}{{b}_{z}}$
$\displaystyle {{c}_{z}}~=\text{ }{{a}_{x}}{{b}_{y}}~-\text{ }{{a}_{y}}{{b}_{x}}$
Dónde:
$\displaystyle \begin{array}{l}{{a}_{x}}=1\\{{a}_{y}}=2\\{{a}_{z}}=3\end{array}$
y
$\displaystyle \begin{array}{l}{{b}_{x}}=4\\{{b}_{y}}=5\\{{b}_{z}}=6\end{array}$
Entonces:
$\displaystyle {{c}_{x}}={{a}_{y}}{{b}_{z}}-{{a}_{z}}{{b}_{y}}=\left( 2 \right)\left( 6 \right)-\left( 3 \right)\left( 5 \right)=12-15=-3$
$\displaystyle {{c}_{y}}={{a}_{z}}{{b}_{x}}-{{a}_{x}}{{b}_{z}}=\left( 3 \right)\left( 4 \right)-\left( 1 \right)\left( 6 \right)=12-6=6$
$\displaystyle {{c}_{z}}={{a}_{x}}{{b}_{y}}-{{a}_{y}}{{b}_{x}}=\left( 1 \right)\left( 5 \right)-\left( 2 \right)\left( 4 \right)=5-8=-3$
Por lo que el resultado del producto cruz, es: (-3, 6, -3)
Problema 4. Cual es el producto cruz de a = (-2, 3, 5) y b = (-4, 1, -6)
Solución:
Este problema es similar al anterior, en un espacio 3D, por lo que recurrimos a aplicar la misma fórmula, dónde:
$\displaystyle \begin{array}{*{20}{l}} {{{a}_{x}}=-2} \\ {{{a}_{y}}=3} \\ {{{a}_{z}}=5} \end{array}$
y
$\displaystyle \begin{array}{*{20}{l}} {{{b}_{x}}=-4} \\ {{{b}_{y}}=1} \\ {{{b}_{z}}=-6} \end{array}$
Entonces:
$\displaystyle {{c}_{x}}={{a}_{y}}{{b}_{z}}-{{a}_{z}}{{b}_{y}}=\left( 3 \right)\left( {-6} \right)-\left( 5 \right)\left( 1 \right)=-18-5=-23$
$\displaystyle {{c}_{y}}={{a}_{z}}{{b}_{x}}-{{a}_{x}}{{b}_{z}}=\left( 5 \right)\left( {-4} \right)-\left( {-2} \right)\left( {-6} \right)=-20-12=-32$
$\displaystyle {{c}_{z}}={{a}_{x}}{{b}_{y}}-{{a}_{y}}{{b}_{x}}=\left( {-2} \right)\left( 1 \right)-\left( 3 \right)\left( {-4} \right)=-2-(-12)=10$
Por lo que el resultado del producto cruz es (-23, -32, 10)
Temas que podrían interesarte 👇