Propiedades de los límites

Un limite en cálculo diferencial es una herramienta matemática usada para determinar el comportamiento de una función en un punto dado. Más específicamente, un límite de una función en un punto es el valor que la función se acerca a cuando se aproxima al punto desde los lados izquierdo y derecho. Esto se usa para estudiar la variación de una función y para también un gran uso en el cálculo de los límites de integrales, tema que se verá más adelante en la plataforma.

Notación de Límite

El límite de una función se designa por $\displaystyle f(x)\to L$ cuando $\displaystyle x\to a$ a o usando la notación de límite:

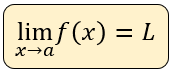
Regla de la suma

Esta regla establece que el límite de la suma de dos funciones es igual a la suma de sus límites:

$\displaystyle \underset{{x\to a}}{\mathop{{\lim }}}\,\left[ {f\left( x \right)+g\left( x \right)} \right]=\underset{{x\to a}}{\mathop{{\lim }}}\,f\left( x \right)+\underset{{x\to a}}{\mathop{{\lim }}}\,g\left( x \right)$

Regla de la suma extendida

En dado caso que tengamos más límites de funciones sumándose, entonces aplicamos:

$\displaystyle \underset{{x\to a}}{\mathop{{\lim }}}\,\left[ {{{f}_{1}}\left( x \right)+\ldots +{{f}_{n}}\left( x \right)} \right]=\underset{{x\to a}}{\mathop{{\lim }}}\,{{f}_{1}}\left( x \right)+\ldots +\underset{{x\to a}}{\mathop{{\lim }}}\,{{f}_{n}}\left( x \right)$

Regla de la función constante

El límite de una constante por una función es igual al producto de la constante y el límite de la función:

$\displaystyle \underset{{x\to a}}{\mathop{{\lim }}}\,C=C$

Regla del múltiplo constante

El límite de una constante por una función es igual al producto de la constante y el límite de la función:

$\displaystyle \underset{{x\to a}}{\mathop{{\lim }}}\,kf\left( x \right)=k\underset{{x\to a}}{\mathop{{\lim }}}\,f\left( x \right)$

Regla del producto

Esta regla dice que el límite del producto de dos funciones es el producto de sus límites (si existen):

$\displaystyle \underset{{x\to a}}{\mathop{{\lim }}}\,\left[ {f\left( x \right)g\left( x \right)} \right]=\underset{{x\to a}}{\mathop{{\lim }}}\,f\left( x \right)\cdot \underset{{x\to a}}{\mathop{{\lim }}}\,g\left( x \right)$

Regla del producto extendida

En dado caso que tengamos que calcular el límite de muchos productos, entonces aplicaremos:

$\displaystyle \underset{{x\to a}}{\mathop{{\lim }}}\,\left[ {{{f}_{1}}\left( x \right){{f}_{2}}\left( x \right)\cdots {{f}_{n}}\left( x \right)} \right]=\underset{{x\to a}}{\mathop{{\lim }}}\,{{f}_{1}}\left( x \right)\cdot \underset{{x\to a}}{\mathop{{\lim }}}\,{{f}_{2}}\left( x \right)\cdots \underset{{x\to a}}{\mathop{{\lim }}}\,{{f}_{n}}\left( x \right)$

Regla del cociente

Cuando tenemos que calcular el límite del cociente de dos funciones, entonces obtenemos el cociente de sus límites, siempre que el límite de la función del denominador no sea cero:

$\displaystyle \underset{{x\to a}}{\mathop{{\lim }}}\,\frac{{f\left( x \right)}}{{g\left( x \right)}}=\frac{{\underset{{x\to a}}{\mathop{{\lim }}}\,f\left( x \right)}}{{\underset{{x\to a}}{\mathop{{\lim }}}\,g\left( x \right)}}$

Solamente si:

$\displaystyle \underset{{x\to a}}{\mathop{{\lim }}}\,g(x)\ne 0$

Regla de potencia

Para el límite de una función elevada a una potencia, se efectúa lo siguiente:

$\displaystyle \underset{{x\to a}}{\mathop{{\lim }}}\,{{\left[ {f\left( x \right)} \right]}^{p}}={{\left[ {\underset{{x\to a}}{\mathop{{\lim }}}\,f\left( x \right)} \right]}^{p}}$

Donde la potencia "p" puede ser cualquier número real, en particular,

$\displaystyle \underset{{x\to a}}{\mathop{{\lim }}}\,\sqrt[p]{{f\left( x \right)}}=\sqrt[p]{{\underset{{x\to a}}{\mathop{{\lim }}}\,f\left( x \right)}}$

Si $\displaystyle f(x)={{x}^{n}}$ , entonces

$\displaystyle \underset{{x\to a}}{\mathop{{\lim }}}\,{{x}^{n}}={{a}^{n}},n=0,\pm 1,\pm 2,\ldots $

$\displaystyle a\ne 0$ , si $\displaystyle n\le 0$

Este es un caso especial e la propiedad anterior.

Límite de una función exponencial

$\displaystyle \underset{{x\to a}}{\mathop{{\lim }}}\,{{b}^{{f\left( x \right)}}}={{b}^{{\underset{{x\to a}}{\mathop{{\lim }}}\,f\left( x \right)}}}$

donde la base $\displaystyle b>0$

Límite de un logaritmo de una función

$\displaystyle \underset{{x\to a}}{\mathop{{\lim }}}\,\left[ {{{{\log }}_{b}}f\left( x \right)} \right]={{\log }_{b}}\left[ {\underset{{x\to a}}{\mathop{{\lim }}}\,f\left( x \right)} \right]$

donde la base $\displaystyle b>0$

Teorema del Emparedado o Sandwich

El teorema del emparedado o sandwich afirma que si una función f(x) se encuentra entre dos funciones g(x) y h(x) y los límites de cada una de g(x) y h(x) en un punto dado son iguales (a L), entonces el límite de f(x) en ese punto también es igual a L. Esto se parece a lo que ya sabemos en álgebra. Si a ≤ b ≤ c y a = c entonces b también es igual a c. El teorema entonces nos dice que esta regla también se aplica a los límites.

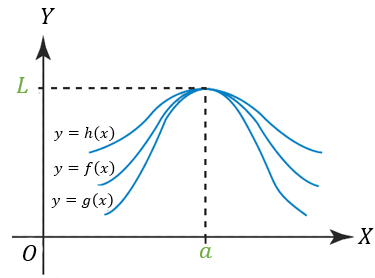
$\displaystyle \underset{{x\to a}}{\mathop{{\lim }}}\,g\left( x \right)=\underset{{x\to a}}{\mathop{{\lim }}}\,h\left( x \right)=L$

Entonces

$\displaystyle \underset{{x\to a}}{\mathop{{\lim }}}\,f\left( x \right)=L$

La idea aquí es que la función se "apachurre" o "apriete" entre otras dos funciones que tienen el mismo límite.

📄 Ejercicios Resueltos de Límites

Solución:

Observemos que se trata de una multiplicación o producto:

$\displaystyle \underset{{x\to 10}}{\mathop{{\lim }}}\,\left( {2x\log {{x}^{3}}} \right)=\underset{{x\to 10}}{\mathop{{\lim }}}\,2x\cdot \underset{{x\to 10}}{\mathop{{\lim }}}\,\log {{x}^{3}}$

Aplicando las propiedades:

$\displaystyle \underset{{x\to 10}}{\mathop{{\lim }}}\,\left( {2x\log {{x}^{3}}} \right)=2\underset{{x\to 10}}{\mathop{{\lim }}}\,x\cdot \log \left( {\underset{{x\to 10}}{\mathop{{\lim }}}\,{{x}^{3}}} \right)$

$\displaystyle \underset{{x\to 10}}{\mathop{{\lim }}}\,\left( {2x\log {{x}^{3}}} \right)=2(10)\cdot \log \left( {1000} \right)$

$\displaystyle \underset{{x\to 10}}{\mathop{{\lim }}}\,\left( {2x\log {{x}^{3}}} \right)=2(10)\left( 3 \right)=60$

Esto da como resultado:

$\displaystyle \underset{{x\to 10}}{\mathop{{\lim }}}\,\left( {2x\log {{x}^{3}}} \right)=60$

Solución:

Aplicando las propiedades de los límites de suma, producto, y cociente, nosotros obtenemos:

$\displaystyle \underset{{x\to 9}}{\mathop{{\lim }}}\,\frac{{4{{x}^{2}}}}{{1+\sqrt{x}}}=\frac{{\underset{{x\to 9}}{\mathop{{\lim }}}\,4{{x}^{2}}}}{{\underset{{x\to 9}}{\mathop{{\lim }}}\,\left( {1+\sqrt{x}} \right)}}$

Luego

$\displaystyle \underset{{x\to 9}}{\mathop{{\lim }}}\,\frac{{4{{x}^{2}}}}{{1+\sqrt{x}}}=\frac{{4\underset{{x\to 9}}{\mathop{{\lim }}}\,{{x}^{2}}}}{{\underset{{x\to 9}}{\mathop{{\lim }}}\,1+\underset{{x\to 9}}{\mathop{{\lim }}}\,\sqrt{x}}}$

y finalmente obtenemos:

$\displaystyle \underset{{x\to 9}}{\mathop{{\lim }}}\,\frac{{4{{x}^{2}}}}{{1+\sqrt{x}}}=\frac{{4\cdot {{9}^{2}}}}{{1+\sqrt{9}}}=81$

Solución:

Aplicando las propiedades:

$\displaystyle \underset{{x\to 1}}{\mathop{{\lim }}}\,\frac{{g\left( x \right)-3f\left( x \right)}}{{{{f}^{2}}\left( x \right)+g\left( x \right)}}=\frac{{\underset{{x\to 1}}{\mathop{{\lim }}}\,\left[ {g\left( x \right)-3f\left( x \right)} \right]}}{{\underset{{x\to 1}}{\mathop{{\lim }}}\,\left[ {{{f}^{2}}\left( x \right)+g\left( x \right)} \right]}}$

Aplicando de manera individual los límites:

$\displaystyle \underset{{x\to 1}}{\mathop{{\lim }}}\,\frac{{g\left( x \right)-3f\left( x \right)}}{{{{f}^{2}}\left( x \right)+g\left( x \right)}}=\frac{{\underset{{x\to 1}}{\mathop{{\lim }}}\,g\left( x \right)-\underset{{x\to 1}}{\mathop{{\lim }}}\,\left[ {3f\left( x \right)} \right]}}{{\underset{{x\to 1}}{\mathop{{\lim }}}\,{{f}^{2}}\left( x \right)+\underset{{x\to 1}}{\mathop{{\lim }}}\,g(x)}}$

Con esto obtenemos:

$\displaystyle \underset{{x\to 1}}{\mathop{{\lim }}}\,\frac{{g\left( x \right)-3f\left( x \right)}}{{{{f}^{2}}\left( x \right)+g\left( x \right)}}=\frac{{\underset{{x\to 1}}{\mathop{{\lim }}}\,g\left( x \right)-3\underset{{x\to 1}}{\mathop{{\lim }}}\,f(x)}}{{{{{\left[ {\underset{{x\to 1}}{\mathop{{\lim }}}\,f\left( x \right)} \right]}}^{2}}+\underset{{x\to 1}}{\mathop{{\lim }}}\,g(x)}}$

Ahora si, podemos evaluar el límite, recordando los valores iniciales que nos proporcionaron en el problema:

$\displaystyle \underset{{x\to 1}}{\mathop{{\lim }}}\,\frac{{g\left( x \right)-3f\left( x \right)}}{{{{f}^{2}}\left( x \right)+g\left( x \right)}}=\frac{{3-3\left( 2 \right)}}{{{{2}^{2}}+3}}=\frac{{3-6}}{{4+3}}=-\frac{3}{7}$

Por lo tanto, obtenemos -3/7 como resultado del límite

Solución:

Vamos a partir de un conocimiento que debemos tener hasta ahora respecto a los valores de "x" que puede tomar el coseno, $\displaystyle -1\le \cos x\le 1$ para todo x, entonces:

$\displaystyle 3x-1\le 3x+\cos x\le 3x+1$

Diviendiendo por 2x - 7 >0 , nosotros obtenemos:

$\displaystyle \frac{{3x-1}}{{2x-7}}\le \frac{{3x+\cos x}}{{2x-7}}\le \frac{{3x+1}}{{2x-7}}$

Como consideramos a "x" un valor grande y positivo, por tanto 2x-7>0, no cambiamos los signos de desigualdad. Entonces

$\displaystyle \underset{{x\to \infty }}{\mathop{{\lim }}}\,\frac{{3x-1}}{{2x-7}}\le \underset{{x\to \infty }}{\mathop{{\lim }}}\,\frac{{3x+\cos x}}{{2x-7}}\le \underset{{x\to \infty }}{\mathop{{\lim }}}\,\frac{{3x+1}}{{2x-7}}$

Calculando el límite por izquierda

$\displaystyle \underset{{x\to \infty }}{\mathop{{\lim }}}\,\frac{{3x-1}}{{2x-7}}=\underset{{x\to \infty }}{\mathop{{\lim }}}\,\frac{{3-\frac{1}{x}}}{{2-\frac{7}{x}}}=\frac{3}{2}$

Calculando el límite por derecha

$\displaystyle \underset{{x\to \infty }}{\mathop{{\lim }}}\,\frac{{3x+1}}{{2x-7}}=\underset{{x\to \infty }}{\mathop{{\lim }}}\,\frac{{3+\frac{1}{x}}}{{2-\frac{7}{x}}}=\frac{3}{2}$

Del teorema del sandwich o emparedado, podemos decir entonces que:

$\displaystyle \underset{{x\to \infty }}{\mathop{{\lim }}}\,\frac{{3x+\cos x}}{{2x-7}}=\frac{3}{2}$