Regla de los 4 (cuatro) pasos - Ejercicios Resueltos

Heyyy!! En el artículo nuevo de hoy hablaremos sobre el cálculo diferencial, cuando se inicia el tema de derivadas y su interpretación geométrica, escucharás el tema sobre la "Regla de los Cuatro Pasos" que consiste en encontrar la derivada de cualquier función a partir de su definición 😎

Introducción a la Derivada por Definición

Al principio puede ser una tarea muy tediosa, pero es esencial para poder comprender el origen de la derivada de cualquier función, seguramente también te estarás preguntando ¿Por qué no solamente utilizar las fórmulas?, es correcto; pero sin la regla de los cuatro pasos no habría derivada alguna, pues todas proceden de ahí, es por eso que se necesita comprender al menos el concepto y de ahí realizar derivadas para poder practicar, para ello empezaremos conociendo el problema fundamental.

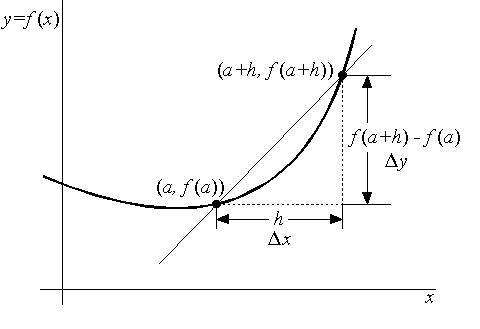
A partir de esas dudas se concluyó lo siguiente:

$\displaystyle \underset{h\to 0}{\mathop{\lim }}\,\frac{f(x+h)-f(x)}{h}$

No es difícil de interpretar, y de aquí surge todo, observa:

• Sumamos el incremento (paso 1)

$\displaystyle f(x+h)$

• Restamos la función original (paso 2)

$\displaystyle -f(x)$

• Dividimos entre el incremento (paso 3)

$\displaystyle h$

• Evaluamos el límite cuando se tiende a cero (paso 4)

$\displaystyle \underset{h\to 0}{\mathop{\lim }}\,$

En otros casos, también puedes ver la derivada usando incrementos.. Pero es lo mismo, exactamente lo mismo.

$\displaystyle \underset{\Delta x\to 0}{\mathop{\lim }}\,\frac{f(x+\Delta x)-f(x)}{\Delta x}$

Pero para entenderlo mejor, veamos con algunos ejemplos.

Regla de los 4 pasos - Ejemplos Resueltos

$\displaystyle y=5{{x}^{2}}$

Solución:

Primer paso (incrementamos) ¡¡OJO!! es en ambos lados

$\displaystyle y+\Delta y=5{{(x+\Delta x)}^{2}}$

Segundo paso (restamos la función original)

$\displaystyle y+\Delta y-y=5{{(x+\Delta x)}^{2}}-5{{x}^{2}}$

Podemos seguir haciendo el otro paso, pero no tendría caso si lo hacemos ya que debemos dejar clara la expresión que tenemos hasta ahora, y es momento para desarrollar el binomio al cuadrado, así que:

$\displaystyle \Delta y=5({{x}^{2}}+2x\Delta x+\Delta {{x}^{2}})-5{{x}^{2}}$

Propiedad distributiva

$\displaystyle \Delta y=5{{x}^{2}}+10x\Delta x+5\Delta {{x}^{2}}-5{{x}^{2}}$

$\displaystyle \Delta y=10x\Delta x+5\Delta {{x}^{2}}$

-Tercer paso (dividimos entre delta de X)

$\displaystyle \frac{\Delta y}{\Delta x}=\frac{10x\Delta x+5\Delta {{x}^{2}}}{\Delta x}$

$\displaystyle \frac{\Delta y}{\Delta x}=10x+5\Delta x$

Cuarto paso (evaluamos el límite)

$\displaystyle \underset{\Delta x\to 0}{\mathop{\lim }}\,\frac{\Delta y}{\Delta x}=\underset{\Delta x\to 0}{\mathop{\lim }}\,\left( 10x+5\Delta x \right)$

Resultado:

$\displaystyle y'=\underset{\Delta x\to 0}{\mathop{\lim }}\,\frac{\Delta y}{\Delta x}=10x$

Por lo que la derivada es 10x. ¡¡Fácil!!, Pero si te quedaron dudas, intenta ver el siguiente vídeo explicado paso a paso de este mismo ejemplo.

Lo hagamos ahora un poco más rápido con otro ejemplo

$\displaystyle y=\frac{3x+2}{2x-1}$

Solución

• Anotamos todos los pasos, pero iremos resolviendo paso a paso:

$\displaystyle \underset{\Delta x\to 0}{\mathop{\lim }}\,\frac{\frac{3(x+\Delta x)+2}{2x+2\Delta x-1}-\frac{3x+2}{2x-1}}{\Delta x}$

$\displaystyle \underset{\Delta x\to 0}{\mathop{\lim }}\,\frac{\frac{3x+3\Delta x+2}{2x+2\Delta x-1}-\frac{3x+2}{2x-1}}{\Delta x}$

$\displaystyle \underset{\Delta x\to 0}{\mathop{\lim }}\,\frac{\frac{(2x+1)(3x+3\Delta x+2)-(3x+2)(2x+2\Delta x-1)}{\left( 2x+2\Delta x-1 \right)\left( 2x-1 \right)}}{\Delta x}$

Seguimos reduciendo.

Pero observa lo que nos ha quedado en el numerador:

$\displaystyle \frac{{(2x-1)(3x+3\Delta x+2)-(3x+2)(2x+2\Delta x-1)}}{{\left( {2x+2\Delta x-1} \right)\left( {2x-1} \right)}}$

$\displaystyle \frac{-7\Delta x}{\left( 2x+2\Delta x-1 \right)\left( 2x-1 \right)}$

Ahora si lo colocamos en nuestro límite

$\displaystyle \underset{\Delta x\to 0}{\mathop{\lim }}\,\frac{\frac{-7\Delta x}{\left( 2x+2\Delta x-1 \right)\left( 2x-1 \right)}}{\Delta x}$

Que es lo mismo escribirlo de la siguiente manera:

$\displaystyle \underset{\Delta x\to 0}{\mathop{\lim }}\,\frac{-7\Delta x}{\Delta x\left( 2x+2\Delta x-1 \right)\left( 2x-1 \right)}$

Simplificando

$\displaystyle \underset{\Delta x\to 0}{\mathop{\lim }}\,\frac{-7}{\left( 2x+2\Delta x-1 \right)\left( 2x-1 \right)}$

Evaluando el límite

$\displaystyle y'=\underset{\Delta x\to 0}{\mathop{\lim }}\,\frac{-7}{\left( 2x-1 \right)\left( 2x-1 \right)}=-\frac{7}{{{(2x-1)}^{2}}}$

Por lo que la derivada es:

Resultado:

$\displaystyle y'=-\frac{7}{{{(2x-1)}^{2}}}$

Y que pasa si probamos con una raíz....

$\displaystyle y=\sqrt{x+5}$

Solución:

Al poner los 4 pasos juntos, tenemos:

$\displaystyle y'=\underset{\Delta x\to 0}{\mathop{\lim }}\,\frac{\sqrt{x+\Delta x+5}-\sqrt{x+5}}{\Delta x}$

Tenemos que racionalizar, para poder simplificar el cálculo.

$\displaystyle y'=\underset{\Delta x\to 0}{\mathop{\lim }}\,\frac{\sqrt{x+\Delta x+5}-\sqrt{x+5}}{\Delta x}\cdot \frac{\sqrt{x+\Delta x+5}+\sqrt{x+5}}{\sqrt{x+\Delta x+5}+\sqrt{x+5}}$

De ahí tenemos:

$\displaystyle y'=\underset{\Delta x\to 0}{\mathop{\lim }}\,\frac{{{\left( \sqrt{x+\Delta x+5} \right)}^{2}}-{{\left( \sqrt{x+5} \right)}^{2}}}{\Delta x\left( \sqrt{x+\Delta x+5}+\sqrt{x+5} \right)}$

Luego...

$\displaystyle y'=\underset{\Delta x\to 0}{\mathop{\lim }}\,\frac{x+\Delta x+5-x-5}{\Delta x\left( \sqrt{x+\Delta x+5}+\sqrt{x+5} \right)}$

Por lo que:

$\displaystyle y'=\underset{\Delta x\to 0}{\mathop{\lim }}\,\frac{\Delta x}{\Delta x\left( \sqrt{x+\Delta x+5}+\sqrt{x+5} \right)}=\underset{\Delta x\to 0}{\mathop{\lim }}\,\frac{1}{\sqrt{x+\Delta x+5}+\sqrt{x+5}}$

Evaluamos el límite y eso nos da:

Resultado:

$\displaystyle y'=\frac{1}{2\sqrt{x+5}}$

Por lo que vendría a ser la derivada de la función original...

Si se observa no es en lo absoluto complicado, ahora es momento de practicar.

🟠 Resolver los siguientes ejercicios

Ahora es momento de practicar, acá abajo están algunos ejercicios con sus respectivas soluciones paso a paso. 😀

👉 Ver Solución

2.- $\displaystyle y=\frac{3{{x}^{2}}+1}{2x}$

3.- $\displaystyle y=\sqrt{x-3}$

4.- $\displaystyle y=\sqrt{\frac{x+6}{x+1}}$