Segunda Ley de la Termodinámica - Ejercicios Resueltos

¡Buenas amigos! tiene días que no publico un post, pero es porque estamos trabajando en grandes cosas para este sitio así como en otros de la misma índole, así que no te preocupes y si ya eres un suscriptor más, dentro de poco recibirás buenas noticias 😎
En esta ocasión vengo con un post muy entretenido e interesante en el mundo de la física, así que presta mucha atención si quieres aprender, consultar o simplemente reafirmar tus conocimientos de este tema, ya que veremos algunos ejercicios resueltos y de que forma entender por completo la segunda ley de la termodinámica.
? ¿Qué nos dice la segunda ley de la termodinámica?
Antes de entrar a fondo con la segunda ley de la termodinámica, en la primera ley de la termodinámica se explica que la energía no se crea ni se destruye, solo se transforma. La segunda ley, sin embargo es probablemente la más conocida y de caso de estudio más profundo, ya que describe incluso los límites del universo, así como también nos advierte que el tiempo sigue una flecha de sola una dirección y que nuestro universo tiene un destino desolador y catastrófico.
Pero bien, esto puede resultar un poco confuso y quizá no logres captarlo a la primera, así que voy a intentar explicarlo de una manera concisa para comprender esta ley.
La segunda ley de la termodinámica nos dice que:
Es decir, que por ejemplo; si aventamos un vaso de cristal al suelo, este objeto "se romperá" y se dispersará en fragmentos sobre todo el piso, entonces aquí viene la pregunta. ¿Es posible qué de forma natural los fragmentos se reconstruyan nuevamente a la forma original que tenía antes el vaso?, es lógico que la respuesta sea NO, ya que se trata de un fenómeno irreversible, entonces aquí es donde viene el concepto y estudio de la segunda ley 🙂
Otra forma de encontrarla es mediante una definición similar a la siguiente:
Esto es algo que en su momento podría parecer ilógico, pero si se analiza delicadamente podremos tener una respuesta más teórica y entendible del tema, en algunos casos nos toparemos con la definición de que, "la cantidad de entropía en el universo tiende a incrementarse con el tiempo".
Pero... ¿Qué es entropía? Pues bien, la entropía no es más que aquella cantidad de energía que no se puede aprovechar para producir un trabajo. Así también nos explica que se trata de un desorden total de las moléculas que esto complementa.
Por ejemplo; el universo constantemente se expande y por su desorden considerablemente va aumentando su entropía, hasta quedar sin energía necesaria para seguir transformándose, cuando ese momento llegue, todos los cuerpos alcanzarán un equilibrio térmico, de tal manera que sería el fin del universo entero.
curioso ¿no?
? El estudio de las Máquinas Térmicas
A pesar de estas ideas y teorías que quizá un poco confusas para las personas que no eran científicos en ese tiempo, el avance de la termodinámica se formuló en un momento de gran optimismo tecnológico, con la llegada de la revolución industrial.
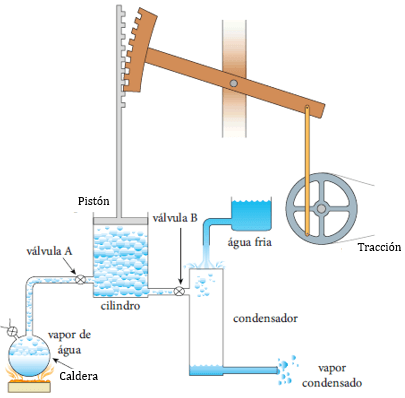
En la mitad del siglo 19, los físicos e ingenieros estaban construyendo máquinas de vapor para mecanizar el trabajo y el transporte y estaban tratando de encontrar la manera de hacerlos más potentes y eficientes. Grandes científicos como Clausius, Kelvin, Joule contribuyeron en gran medida, aunque en cierta parte se le considera como padre de esta disciplina al físico francés Sadi Carnot .
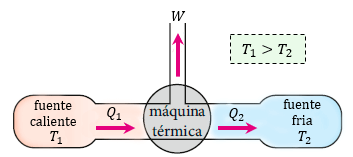
Carnot demostró que se podía predecir la eficiencia máxima teórica de un motor de vapor mediante la medición de la diferencia de temperaturas del vapor en el interior del cilindro y la del aire que lo rodea, conocida en términos termodinámicos como los depósitos de agua caliente y fría de un sistema, respectivamente.
? Fórmula de la Segunda Ley de la Termodinámica
Como se comentó texto atrás, "Es imposible construir una máquina térmica que transforme en su totalidad el calor en energía y viceversa".
La Eficiencia de una máquina térmica es la relación entre el trabajo mecánico producido y el calor suministrado. Y podemos encontrarla de diversas formas:
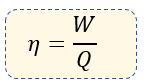
Dónde:
$\displaystyle W=$ Trabajo Mecánico [Cal, Joules]
$\displaystyle Q=$ Calor suministrado a la máquina por el combustible en calorías (cal) o en Joules (J)
$\displaystyle \eta $ = Eficiencia de la máquina térmica
También la podemos encontrar de la siguiente manera:
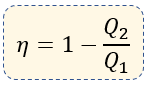
Dónde:
$\displaystyle {{Q}_{1}}=$ Calor Suministrado [Cal, Joules]
$\displaystyle {{Q}_{2}}=$ Calor Obtenido [Cal, Joules]
La eficiencia de una máquina térmica se puede calcular también en función de la relación que hay entre la temperatura de la fuente caliente (T1) y la fuente fría (T2), ambas medidas en temperaturas absolutas, es decir, en grados Kelvin (K) dónde:
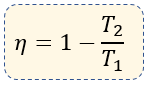
? Ejercicios Resueltos de eficiencia de máquinas térmicas
Veamos algunos ejemplos de la segunda ley de la termodinámica o de máquinas térmicas para comprender mejor el tema 😀
Solución:
Sin duda el problema es muy fácil de resolver, pero antes de poder realizar el cálculo en la fórmula, tenemos que convertir las calorías en Joules, y nos referimos a las calorías que se suministran:
$\displaystyle {{Q}_{1}}=8000cal\left( \frac{4.2J}{1cal} \right)=33600J$
Ahora si podemos sustituir nuestros datos en la fórmula:
$\displaystyle \eta =1-\frac{{{Q}_{2}}}{{{Q}_{1}}}$
Sustituyendo nuestros datos:
$\displaystyle \eta =1-\frac{{{Q}_{2}}}{{{Q}_{1}}}=1-\frac{25200J}{33600J}=1-0.75$
$\displaystyle \eta =1-0.75=0.25$
El valor de 0.25 lo multiplicamos por 100, para obtener el porcentaje de la eficiencia térmica:
$\displaystyle \eta =100\left( 0.25 \right)=25%$
Lo que sería equivalente a un 25% de eficiencia térmica
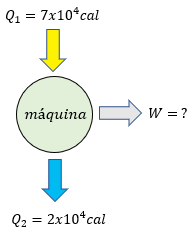
Solución:
Vamos a utilizar nuestros datos de la siguiente manera:
$\displaystyle {{Q}_{1}}=5.8x{{10}^{8}}cal$ (Calor suministrado a la máquina)
$\displaystyle W=8.3x{{10}^{7}}J$ (Trabajo realizado por la máquina)
Convertimos las calorías en Joules, haciendo este pequeño factor de conversión 1 Cal = 4.2 J/Cal , de tal manera que ahora $latex \displaystyle {{Q}_{1}}$ , tendrá el siguiente valor:
$\displaystyle {{Q}_{1}}=5.8x{{10}^{8}}cal\left( 4.2\frac{J}{cal} \right)=2.436x{{10}^{9}}J$
Sustituyendo en la fórmula, tendremos:
$\displaystyle \eta =\frac{W}{Q}$
$\displaystyle \eta =\frac{8.3x{{10}^{7}}J}{2.436x{{10}^{9}}J}=0.034$
que multiplicado por 100, tendríamos
$\displaystyle \eta =100\left( 0.034 \right)=3.4%$
Haciendo un total del 3.4% de eficiencia térmica, bajo esas condiciones.
Ahora veamos otro ejemplo de análisis.
Solución:
Si la máquina recibe 100 cal de la fuente caliente quiere decir que:
$\displaystyle Q=100cal\cdot \left( \frac{4.2J}{1cal} \right)=420J$
Ahora por fórmula tenemos:
$\displaystyle \eta =\frac{W}{Q}=\frac{420J}{420J}=1$
que multiplicado por 100, tenemos
$\displaystyle e=1\cdot 100=100%$
Por lo que nuestra respuesta tendrá que ser, que eso es imposible ya que viola la segunda ley de la termodinámica, al decir que una máquina no puede realizar una eficiencia de 100%, puesto que al realizar algún trabajo la energía tiene que disiparse de alguna forma o transformarse en otra cosa.
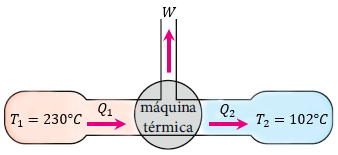
Solución:
Si observamos bien el problema, en este solamente contamos con las temperaturas, pero no contamos con otro tipo de dato. Si leemos muy bien el tema nos daremos cuenta que podemos usar la fórmula de la eficiencia térmica en términos de las temperaturas. Pero primero debemos de convertir las temperaturas en absolutas.
$\displaystyle {{T}_{1}}=427{}^\circ C+273=700K$
$\displaystyle {{T}_{2}}=127{}^\circ C+273=400K$
Aplicando la fórmula de la eficiencia:
$\displaystyle \eta =1-\frac{{{T}_{2}}}{{{T}_{1}}}$
Sustituyendo nuestros datos en la fórmula:
$\displaystyle \eta =1-\frac{400K}{700K}=1-0.57=0.43$
Multiplicando por 100, para convertirlo en porcentaje
$\displaystyle \eta =100\left( 0.43 \right)=43%$
Por lo que la eficiencia es de 43%
? Ejercicios para practicar de la Segunda Ley de la Termodinámica
Ahora es momento de practicar con algunos ejemplos de la segunda ley de la termodinámica, o de máquinas térmicas. Le comentamos que estos ejercicios vienen con la solución paso a paso para corroborar sus resultados ??
-
Me puedes ayudar con esto por favor.
Un panel de prueba de 20.32 x 20.32 cm de grueso, está colocado
entre dos placas, y el conjunto está debidamente aislado. La superficie
de separación (interfaz) de una placa, se mantiene a 79.4 °C mediante
un suministro de energía eléctrica de 50 W; la otra placa posee una
temperatura interfacial de 21.1 °C. Obtenga el valor d la constante K,
para el panel de prueba. -
Un refrigerador es utilizado para mantener una habitación a 50 ºF. Este equipo
toma el calor de la habitación y lo transfiere al aire ambiente que se encuentra a 90
ºF. Para accionarlo se le proporciona toda la potencia producida por una máquina
térmica de Carnot que recibe calor de un depósito a 1850 ºF a una tasa de 650
Btu/min. y rechaza el calor de desecho al mismo aire ambiente a 90ºF. Determinar:
a) La tasa máxima de remoción de calor de la habitación
b) La tasa de calor liberado del aire ambiente -
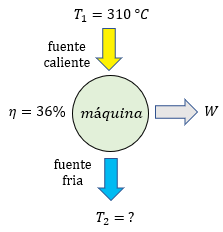
Determina la temperatura que entra el vapor de una máquina térmica si su eficiencia del 80 % y el vapor que sale tiene una temperatura de 75 °C
-
Una maquina térmica usa una fuente fría a 50 °C y tiene una eficiencia ideal de Carnot
de 30 %, ¿Cual deberá ser la temperatura de la fuente fría si se desea aumentar a 40%? -
AYUDA!!!
Una bomba de calor se utiliza para calentar un edificio . La temperatura exterior es de 263.15 K y la temperatura deseada en el interior es de 293.5 K. La pérdida de calor a través de las paredes es de 30 kW. Determine el coeficiente de desempeño y la potencia mínima requerida para operar la bomba de calor para matener el interior del edificio a temperatura constante.
82 Deja tu comentario
Deja una respuesta

Estos temas te pueden interesar