Sistema de Ecuaciones - Método Gráfico

Hoy nos toca hablar sobre los sistema de ecuaciones, y es un tema que muchos deberíamos saber. Pues bien muchos fenómenos del mundo real pueden representarse matemáticamente, y algunos de ellos constituyen problemas lineales, es decir, que involucran el manejo de ecuaciones de primer grado, cuya representación gráfica es una línea recta.

Pues bien, en este post vamos a realizar problemas que pueden representarse como un conjunto de ecuaciones con dos incógnitas que de alguna forma u otra constituyen un sistema de ecuaciones; asó como su solución, a través de diversos métodos. Por ejemplo el método gráfico, método de reducción, método de sustitución, de eliminación y en el blog de Laplacianos vamos a observar también la solución a incógnitas por medio de la regla de Cramer y Gauss Jordan. 😎

Sistema de Ecuaciones con Dos Incógnitas

Consideremos el siguiente problema: Se requiere hallar dos números cuya suma sea igual a 10 ¿cuáles son esos números?

Al plantear algebraicamente el problema, se tiene:

x + y = 10

Porque ambos son dos números cualquiera, o sea dos variables. Pero como no tenemos más información al respecto, los valores de de "x" y "y" pueden tomar cualquier valor que cumpla la condición de ser sumados y dar 10.

Por ejemplo:

x = 3, y = 7 --> x + y = 10

x = 7 , y = 3 --> x + y = 10

x = 15, y = -5 --> x+y = 10

x = 0, y = 10 --> x+y = 10

y así podemos seguir hasta encontrar muchísimos valores tanto para "x" como para "y", y no podríamos ni terminar, por ello se dice que el conjunto solución de este tipo de ecuaciones es infinito.

Función Lineal

Veamos el siguiente vídeo sobre Función Lineal

Hasta ahora hemos podido asociar valores de las variables para un conjunto solución infinito, pero veamos algo más. ¿Qué pasaría si de una ecuación despejamos a una variable?, Por ejemplo en nuestro caso vamos a despejar a "y" de las siguientes ecuaciones con dos variables, si tienes problemas para despejar, te recomiendo leer este artículo Cómo despejar Fórmulas

x + y = 5

"Despejando"

y = 5 - x

--

3x - 4y = 2

"Despejando"

-4y = 2 - 3x

Al despejar la variable y la estamos escribiendo en función de x, es decir, a cada valor que asuma x le corresponde uno de y que es su imagen.

Al representar estas funciones en el plano cartesiano, observamos que son rectas, y a estas mismas se les denomina funciones lineales , por lo que podemos decir que:

Ejercicios Resueltos con sistemas de dos variables

Bien, es momento de ir por los ejemplos resueltos de un sistema de ecuaciones mediante el método gráfico. Ya que sabemos sobre las funciones lineales que representan rectas, entonces no tendremos problema alguno para comprender los siguientes temas; así que prepárate para responder los problemas.

Ejemplo 1: Del siguiente sistema de ecuaciones encuentre los valores de "x" y de "y".

Solución: 

Lo primero que tenemos que hacer es graficar las dos funciones lineales, y si despejamos tendremos algo así:

y = 10 - x (primera ecuación)

-y = 5 - x

y = -5 + x (segunda ecuación)

Al momento de trazar la gráficas correspondientes en cada una de las ecuaciones tendremos algo similar a esto:

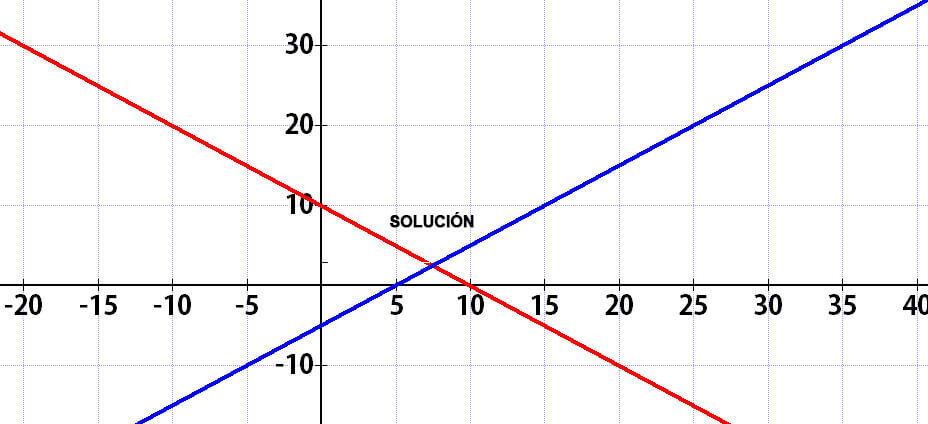
Pues nuestra solución si observamos cae prácticamente en x = 7.5 y en el eje "y" cae en y = 2.5

Esto es fácil de asumir, porque lo único que tenemos que hacer es sustituir los valores en las ecuaciones, por ejemplo:

x + y = 10

7.5 + 2.5 = 10 (se cumple).

--

x - y = 5

7.5 - 2.5 = 5 (se cumple).

Ejemplo 2: Del siguiente sistema de ecuaciones encuentre los valores de "x" y "y" , recuerde hacer la comprobación.

Solución: 

Para representarlo gráficamente , primero efectuamos una tabulación. Recuerda que bastan dos puntos para determinar una recta. Al momento de realizar la gráfica vamos a encontrar lo que buscamos que es precisamente la solución única.

Despejando las variables, tenemos lo siguiente:

y = x - 1 (primera ecuación)

y = -2x +8 (segunda ecuación)

Ahora trazamos la gráfica

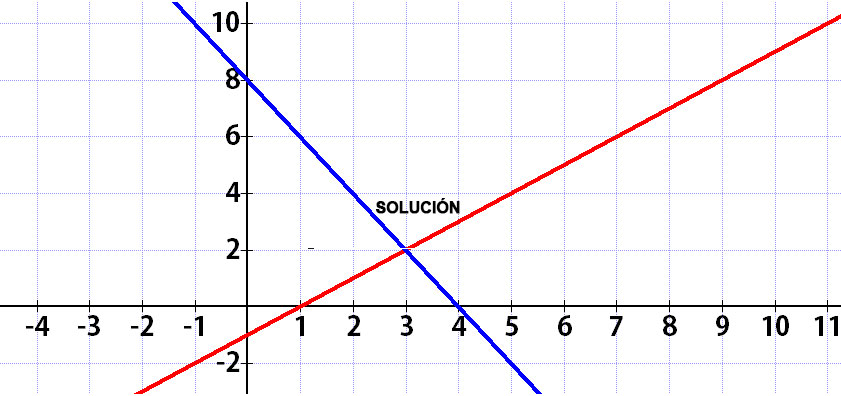
Las soluciones están muy claras, por ejemplo en el eje "x" quedamos en 3, y en el eje "y" quedamos en 2. Por lo tanto nuestro conjunto solución es el par ordenado (3,2).

Ahora hacemos la comprobación.

x - y = 1

sustituyendo

3 -2 = 1 (comprobado).

--

2x + y = 8

2(3) + 2 = 6 +2 = 8 (comprobado).