Sistemas de Coordenadas Rectangulares

En el campo de la geometría analítica los sistemas de coordenadas rectangulares son muy imporantes, pues pertenecen a los lugares geométricos de líneas, rectas y curvas. Recordemos que la geometría analítica posee dos características muy fundamentales, que consisten en; dado un lugar geométrico se puede obtener su ecuación, y dada una ecuación algebraica se puede obtener su lugar geométrico, entonces estamos ante un campo de las matemáticas donde sabemos que tenemos que asociar los lugares geométricos con expresiones numéricas y algebraicas.

Antes de profundizar sobre los sistemas de coordenadas rectangulares, es necesario que tengamos que relacionar los conceptos de un sistema de coordenadas lineales, esto nos ayudará a poder comprender las bases para construir nuevos aprendizajes a partir de la recta numérica y los números reales.

Para escribir la posición de un punto en la recta, por lo general se utiliza la notación P(x), lo cual significa que al punto P le corresponde la coordenada x. Ahora para calcular gráficamente la distancia entre dos puntos en la recta numérica, basta con contar el número de unidades de una posición a otra; algebraicamente se obtiene con mucha facilidad determinando el valor absoluto al restar el valor de la coordenada inicial de la coordenada final. Por ejemplo, si deseamos calcular la distancia entre los puntos $\displaystyle {{P}_{1}}({{x}_{1}})$ y $\displaystyle {{P}_{2}}({{x}_{2}})$, procedemos hacerlo de la siguiente manera:

$\displaystyle d=\left| {{{P}_{1}}{{P}_{2}}} \right|=\left| {{{x}_{2}}-{{x}_{1}}} \right|=\left| {{{x}_{1}}-{{x}_{2}}} \right|$

Ejemplos Resueltos de Coordenadas Lineales

Solución:

Aplicando la fórmula, obtenemos:

$\displaystyle d=\left| {-4-7} \right|=\left| {-11} \right|=11$

Comprobación:

Observa la recta que se presente abajo, y cuenta el número de unidades que hay entre los puntos:

Solución:

Recordar que si aplicamos la fórmula de ambas maneras, los resultados al ser valor absoluto seguirán siendo los mismos:

$\displaystyle d=\left| {5-(-2)} \right|=\left| 7 \right|=7$

o también

$\displaystyle d=\left| {-2-5} \right|=\left| {-7} \right|=7$

Comprobación:

Observe nuevamente la gráfica de los puntos, existen 7 espacios tanto del punto B al A, como del punto A al B.

• Una distancia es una longitud y siempre tiene signo positivo por eso se calcula como el valor absoluto.
• Un segmento dirigido es una longitud con dirección, es decir que puede ser de signo positivo o negativo.

Solución:

Lo primero que haremos será ubicar los puntos en nuestra recta numérica:

Aplicando la fórmula:

$\displaystyle d=\left| {-3-5} \right|=\left| {-8} \right|=8$

o también

$\displaystyle d=\left| {5-(-3)} \right|=\left| 8 \right|=8$

Por lo que tenemos 8 unidades de distancia o espacios tanto del punto C al punto D, como del D al punto C.

Solución:

En este caso utilizaremos dos soluciones para resolver el problema, esto es debido a que la fórmula se puede expresar de dos formas:

Solución A:

$\displaystyle \begin{array}{l}d=\left| {{{x}_{2}}-{{x}_{1}}} \right|=8\\d=\left| {{{x}_{2}}-(-5)} \right|=8\\{{x}_{2}}+5=8\\{{x}_{2}}=8-5\\{{x}_{2}}=3\end{array}$

Solución B:

$\displaystyle \begin{array}{l}d=\left| {{{x}_{1}}-{{x}_{2}}} \right|=8\\d=\left| {-5-{{x}_{2}}} \right|=8\\-5-{{x}_{2}}=8\\-{{x}_{2}}=8+5\\{{x}_{2}}=-13\end{array}$

Comprobación:

Veamos la gráfica:

Observemos que hay 8 espacios tanto del punto $\displaystyle {{{x}_{{2B}}}}$ al punto $\displaystyle {{{x}_{1}}}$ y del punto $\displaystyle {{{x}_{1}}}$ al punto $\displaystyle {{{x}_{{2A}}}}$

El plano cartesiano

Como se explicó anteriormente, los puntos sobre una recta se pueden identificar con números reales al asignarles coordenadas. De manera similar, los puntos sobre un plano pueden identificarse mediante pares ordenados de números reales.

Para extender la utilidad de la correspondencia entre puntos geométricos y números reales, vamos a considerar ahora un punto que se puede moverse en todas direcciones, manteniéndose siempre en un plano. La consecuencia es el sistema coordenado rectangular o cartesiano, llamado asi en honor de su creador René Descartes, un matemático y filósofo francés muy reconocido en el siglo XVII.

1. $\displaystyle P(x,y)$ es un punto geométrico, donde (x,y) representa un par de números reales.
2. $\displaystyle x$ se le llama abscisa, $\displaystyle y$ se llama ordenada; en conjunto, se llaman coordeandas. Al trazarlas en una gráfica, ésta queda dividida en cuatro partes, llamdas cuadrantes, los cuales se designan como, I, II, III, IV, y definen los signos de las coordenadas.

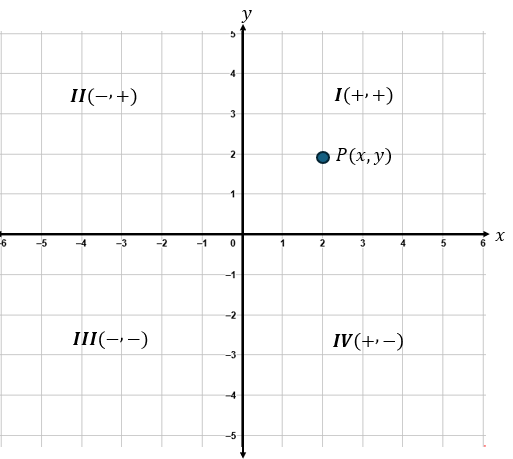
Localizar los puntos en el plano cartesiano 

Vamos a realizar un ejemplo de ubicación de puntos en el plano cartesiano, para entender mucho mejor la ubicación de éstos.

Solución:

1. En cada eje ubicamos la coordenada respectiva.
2. Trazamos por ellas segmentos paralelos a los ejes; en sus intersecciones se encuentran los puntos buscados.
3. Escribe las coordenadas de cada punto.

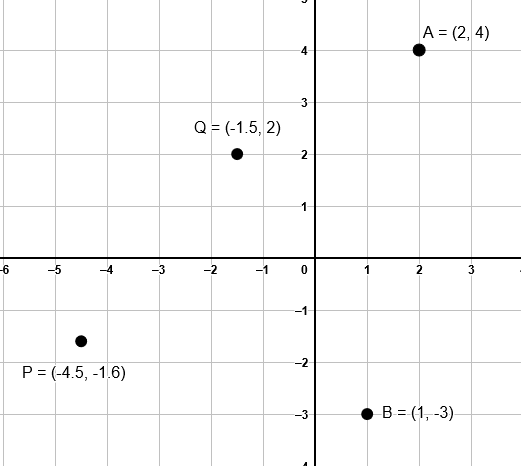
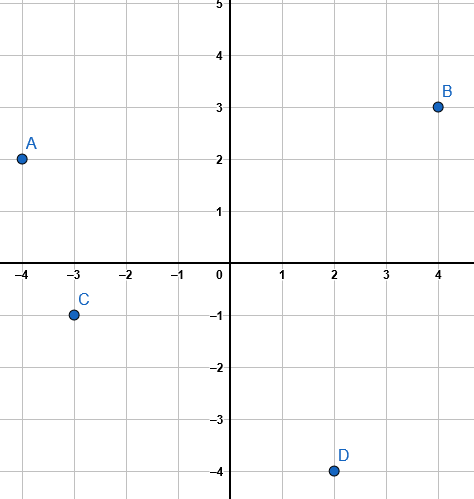
Solución:

Si analizamos bien nuestro plano cartesiano, podremos darnos cuenta que las coordenadas son las siguientes:

$\displaystyle A(-4,2),B(4,3),C(-3,-1),D(2,-4)$

Los Pares Ordenados o Parejas Ordenadas

La pareja ordenada en el sistema de coordenadas cartesianas es aquella que está compuesta por una abscisa y una ordenada. Dispuestas de manera (x,y), se llaman coordenadas. Donde x es la distancia del origen a un punto determinado en el eje x y y es la distancia del origen a punto determinado en el eje y

Ejemplos de parejas ordenadas

1. La pareja ordenada (x,y) tiene como primer elemento a x y como segundo elemento a y
2. La pareja ordenada (3,2) tiene como primer elemento a 3 y como segundo elemento a 2
3. La ecuación y = 2x -1 genera las parejas ordenadas (0, -1) , (2, 3), (-5,-11) y asi sucesivamente.
4. La tabla siguiente muestra las calificaciones de los primeros cinco estudiantes de un grupo.

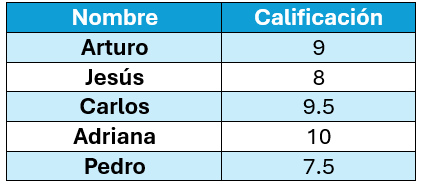
El arreglo en parejas ordeandas queda:

(Arturo, 9) , (Jesús, 8), (Carlos, 9.5), (Adriana, 10), (Pedro, 7.5)

Dos parejas ordenadas son iguales cuando sus primeros elementos son iguales entre si, y cuando sus segundos elementos son iguales entre sí.

1. Si (x,y) = (2,3) significa que x = 2, y = 3
2. $\displaystyle \left( {\sqrt{4},{{3}^{2}}} \right)=\left( {2,9} \right)$ , porque $\displaystyle \sqrt{4}=2$ y $\displaystyle {{3}^{2}}=9$

Veamos algunos ejemplos de localizar los puntos en el plano cartesiano.

Ejercicios Resueltos de Coordenadas Rectángulares

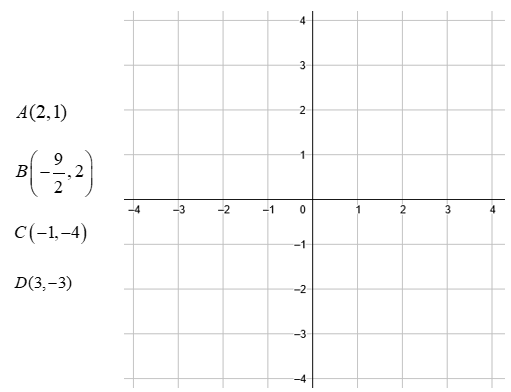
Solución:

La solución a los puntos localizados en el plano cartesiano, serían los siguientes:

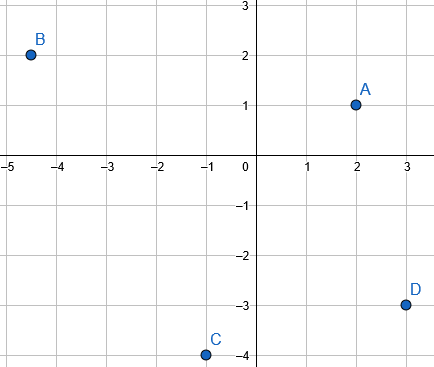
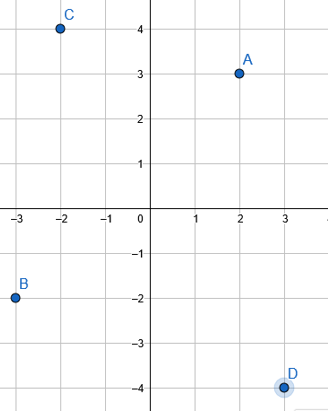
Solución:

Las coordenadas corresponden a los siguientes puntos:

$\displaystyle A(2,3)$

$\displaystyle B(-3,-2)$

$\displaystyle C(-2,4)$

$\displaystyle D(3,-4)$

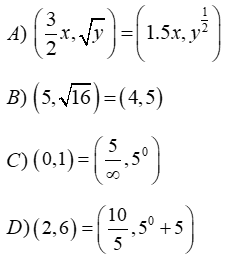
Solución:

a) $\displaystyle (\frac{3}{2}x,\sqrt{y})=(1.5x,{{y}^{{\frac{1}{2}}}})$

Comparando los términos:

PRIMER TÉRMINO
$\displaystyle \frac{3}{2}x=1.5x$

Como 3/2 es igual a 1.5, la igualdad es verdadera.

SEGUNDO TÉRMINO

$\displaystyle \sqrt{y}={{y}^{{\frac{1}{2}}}}$

Como $\displaystyle \sqrt{y}$ escrita en potencias racionales es $\displaystyle {{y}^{{\frac{1}{2}}}}$ la igualdad es correcta. Como ambos términos son iguales, la situación planteada es verdadera.

b) $\displaystyle \left( {5,\sqrt{{16}}} \right)=\left( {4,5} \right)$

Comparando los términos:

PRIMER TÉRMINO

$\displaystyle 5=4$

Como 5 es distinto de 4, la igualdad no existe, como uno de los términos no es igual, la situación planteada es falsa.

c) $\displaystyle (0,1)=\left( {\frac{5}{\infty },{{5}^{0}}} \right)$

Al parecer las parejas ordeandas están en distintos tipos de coordeandas, el pimero en coordenadas rectangulares y el segundo en polares, pero la magnitud del punto en coordenadas polares es cero y el de coordenadas rectangulares es 1, por lo tanto, la situación planteada es falsa.

d) $\displaystyle (2,6)=\left( {\frac{{10}}{5},{{5}^{0}}+5} \right)$

Al parecer las parejas ordenas están en distintos tipos de coordenadas, el primero en coordenadas rectangulares y el segundo en polares, pero la magnitud del punto en coordenadas polares es 2 y el de coordenadas rectangulares es $\displaystyle 2\sqrt{{10}}\left( {\sqrt{{{{6}^{2}}+{{2}^{2}}}}} \right)$ , por lo tanto, la situación planteada es falsa.

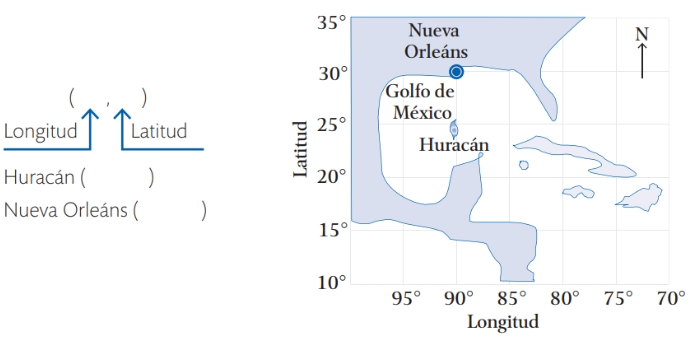
Solución:

Si analizamos perfectamente el diagrama, podemos darnos cuenta que el huracán se encuentra en (90° , 25°) y que Nueva Orleáns está en (90°, 30°).

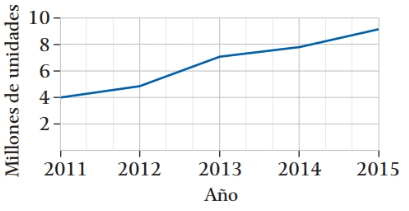
Solución:

Se puede observar que para el 2014, se han llegado a vender cerca de los 8 millones de unidades.