Solucion 1 de Notación Científica

Veamos la solución a los siguientes ejercicios de notación científica. Recuerda que estos son los primeros cuatro ejercicios del tema.

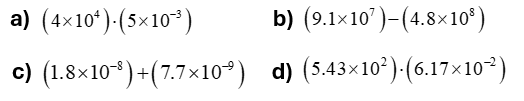
Solución:

a) $\displaystyle \left( {4\times {{{10}}^{4}}} \right)\cdot \left( {5\times {{{10}}^{{-3}}}} \right)$

Realizando la multiplicación:

$\displaystyle \begin{array}{l}\left( {4\times {{{10}}^{4}}} \right)\cdot \left( {5\times {{{10}}^{{-3}}}} \right)=\left( {4\times 5} \right)\times \left( {{{{10}}^{4}}\cdot {{{10}}^{{-3}}}} \right)\\\left( {4\times {{{10}}^{4}}} \right)\cdot \left( {5\times {{{10}}^{{-3}}}} \right)=20\times {{10}^{1}}\\\left( {4\times {{{10}}^{4}}} \right)\cdot \left( {5\times {{{10}}^{{-3}}}} \right)=2\times {{10}^{2}}\end{array}$

b) $\displaystyle \left( {9.1\times {{{10}}^{7}}} \right)-\left( {4.8\times {{{10}}^{8}}} \right)$

Igualando bases:

$\displaystyle \begin{array}{l}\left( {9.1\times {{{10}}^{7}}} \right)-\left( {4.8\times {{{10}}^{8}}} \right)=\left( {9.1\times {{{10}}^{7}}} \right)-\left( {48\times {{{10}}^{7}}} \right)\\\left( {9.1\times {{{10}}^{7}}} \right)-\left( {4.8\times {{{10}}^{8}}} \right)=\left( {9.1-48} \right)\times {{10}^{7}}\\\left( {9.1\times {{{10}}^{7}}} \right)-\left( {4.8\times {{{10}}^{8}}} \right)=-38.9\times {{10}^{7}}\\\left( {9.1\times {{{10}}^{7}}} \right)-\left( {4.8\times {{{10}}^{8}}} \right)=-3.89\times {{10}^{8}}\end{array}$

c) $\displaystyle \left( {1.8\times {{{10}}^{{-8}}}} \right)+\left( {7.7\times {{{10}}^{{-9}}}} \right)$

Igualando bases:

$\displaystyle \left( {1.8\times {{{10}}^{{-8}}}} \right)+\left( {7.7\times {{{10}}^{{-9}}}} \right)=\left( {18\times {{{10}}^{{-9}}}} \right)+\left( {7.7\times {{{10}}^{{-9}}}} \right)$

$\displaystyle \begin{array}{l}\left( {1.8\times {{{10}}^{{-8}}}} \right)+\left( {7.7\times {{{10}}^{{-9}}}} \right)=\left( {18\times {{{10}}^{{-9}}}} \right)+\left( {7.7\times {{{10}}^{{-9}}}} \right)\\\left( {1.8\times {{{10}}^{{-8}}}} \right)+\left( {7.7\times {{{10}}^{{-9}}}} \right)=\left( {18+7.7} \right)\times {{10}^{{-9}}}\\\left( {1.8\times {{{10}}^{{-8}}}} \right)+\left( {7.7\times {{{10}}^{{-9}}}} \right)=25.7\times {{10}^{{-9}}}\\\left( {1.8\times {{{10}}^{{-8}}}} \right)+\left( {7.7\times {{{10}}^{{-9}}}} \right)=2.57\times {{10}^{{-8}}}\end{array}$

d) $\displaystyle \left( {5.43\times {{{10}}^{2}}} \right)-\left( {6.17\times {{{10}}^{{-2}}}} \right)$

Realizando la multiplicación

$\displaystyle \begin{array}{l}\left( {5.43\times {{{10}}^{2}}} \right)-\left( {6.17\times {{{10}}^{{-2}}}} \right)=\left( {5.43\cdot 6.17} \right)\times \left( {{{{10}}^{2}}\times {{{10}}^{{-2}}}} \right)\\\left( {5.43\times {{{10}}^{2}}} \right)-\left( {6.17\times {{{10}}^{{-2}}}} \right)=33.5031\times {{10}^{{2+\left( {-2} \right)}}}\\\left( {5.43\times {{{10}}^{2}}} \right)-\left( {6.17\times {{{10}}^{{-2}}}} \right)=33.5031\times {{10}^{0}}\\\left( {5.43\times {{{10}}^{2}}} \right)-\left( {6.17\times {{{10}}^{{-2}}}} \right)=33.5031\end{array}$

¿Obtuviste los mismos resultados?