Solución 1 Ejercicio Resuelto de Resistencias en Paralelo

En este ejemplo de los problemas resueltos para ejercicios de práctica del tema de Resistencias en Paralelo, es importante tener en cuenta el uso correcto de la fórmula, es por eso que se realizan los ejercicios paso a paso con su solución correspondiente. Recuerde que con este tipo de ejemplos el alumno podrá corroborar su respuesta y verificar si ha llegado al mismo resultado. 😊👇

Nivel de Dificultad: ⭐⭐

Solución:

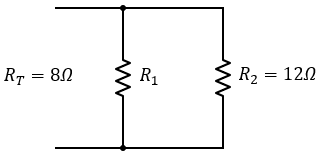
El problema nos pide encontrar el valor de solo una resistencia, dicha resistencia sumada con otra resistencia con valor de 12Ω, da una resistencia equivalente de 8Ω, y no es complicado. Simplemente necesitamos realizar algunos ajustes a nuestra fórmula para solucionar el problema de manera muy sencilla. 😀

• Encontrar el valor de la resistencia R1

Datos:

$\displaystyle {{R}_{T}}=8\Omega $

$\displaystyle {{R}_{2}}=12\Omega $

a) Encontrar el valor de la resistencia R1

Si la fórmula nos enuncia lo siguiente:

$\displaystyle {{R}_{T}}=\frac{1}{{\frac{1}{{{{R}_{1}}}}+\frac{1}{{{{R}_{2}}}}+...+\frac{1}{{{{R}_{n}}}}}}$

Nosotros solamente necesitamos analizar dos resistencias, por lo tanto esto lo podemos reducir a:

$\displaystyle {{R}_{T}}=\frac{1}{\frac{1}{{{R}_{1}}}+\frac{1}{{{R}_{2}}}}$

Que también lo podemos escribir de la siguiente forma:

$\displaystyle \frac{1}{{{R}_{T}}}=\frac{1}{{{R}_{1}}}+\frac{1}{{{R}_{2}}}$

Despejando a R1

$\displaystyle \frac{1}{{{R}_{T}}}-\frac{1}{{{R}_{2}}}=\frac{1}{{{R}_{1}}}$

Invirtiendo la igualdad

$\displaystyle \frac{1}{{{R}_{1}}}=\frac{1}{{{R}_{T}}}-\frac{1}{{{R}_{2}}}$

Ahora si podemos sustituir nuestros datos en la fórmula, quedando así:

$\displaystyle \frac{1}{{{R}_{1}}}=\frac{1}{8\Omega }-\frac{1}{12\Omega }$

Dividiendo.

$\displaystyle \frac{1}{{{R}_{1}}}=0.125\Omega -0.083\Omega =0.042\Omega $

Despejando.

$\displaystyle \frac{1}{0.042\Omega }={{R}_{1}}$

Por lo que el valor de la resistencia 1, es de:

$\displaystyle {{R}_{1}}=\frac{1}{0.042\Omega }=23.8\Omega $

La resistencia 1 deberá tener un valor de 23.8 Ω

Respuesta:

$\displaystyle {{R}_{1}}=23.8\Omega $