Solución 2 Ejercicio Resuelto de Resistencias en Paralelo

De forma similar al ejemplo anterior, en este problema de suma de Resistencias en Paralelo , debemos reforzar el concepto principal que es la utilización correcta de la fórmula, con este ejercicio terminará de comprender la fórmula para poder sumar resistencias en paralelo, no olvide que con estos ejercicios se proporciona la solución paso a paso del ejemplo y nuevamente el alumno comprueba sus resultados de manera correcta y concisa. 😊👇

Nivel de Dificultad: ⭐⭐

Problema 5. Calcular la resistencia equivalente de tres resistencia cuyos valores son R1 = 3Ω, R2 = 6Ω y R3 = 8Ω, conectadas primero a) en serie, b) en paralelo

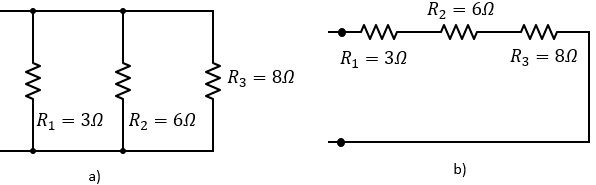
Problema de Resistencias en Paralelo

Solución:

En este problema se pretende que se entienda que la suma de resistencias en serie como la suma de resistencias en paralelo no son lo mismo. Y que la configuración de las resistencias nos proporcionan valores de una resistencia equivalente muy diferentes. La solución de estos problemas es muy sencilla, veamos la solución a estos problemas.

Obtener la suma de resistencias en paralelo
Obtener la suma de resistencias en serie

Datos:

$\displaystyle {{R}_{1}}=3\Omega$

$\displaystyle {{R}_{2}}=6\Omega$

$\displaystyle {{R}_{3}}=8\Omega$

a) Obtener la suma de resistencias en paralelo

Nuevamente, colocamos la fórmula a utilizar:

$\displaystyle {{R}_{T}}=\frac{1}{\frac{1}{{{R}_{1}}}+\frac{1}{{{R}_{2}}}+\frac{1}{{{R}_{3}}}}$

Esta fórmula también la podemos colocar de esta forma:

$\displaystyle \frac{1}{{{R}_{T}}}=\frac{1}{{{R}_{1}}}+\frac{1}{{{R}_{2}}}+\frac{1}{{{R}_{3}}}$

Sustituyendo nuestros datos en la fórmula:

$\displaystyle \frac{1}{{{R}_{T}}}=\frac{1}{3\Omega }+\frac{1}{6\Omega }+\frac{1}{8\Omega }$

Dividiendo cada término:

$\displaystyle \frac{1}{{{R}_{T}}}=0.333\Omega +0.166\Omega +0.125\Omega$

Sumando

$\displaystyle \frac{1}{{{R}_{T}}}=0.624\Omega$

Esto es lo mismo si hacemos que:

$\displaystyle {{R}_{T}}=\frac{1}{0.624\Omega }$

Dividiendo tenemos

$\displaystyle {{R}_{T}}=1.6\Omega$

Es decir 1.6Ω de Resistencia equivalente

b) Obtener la suma de resistencias en serie

La suma de resistencias en paralelo es de la siguiente manera:

$\displaystyle {{R}_{T}}={{R}_{1}}+{{R}_{2}}+{{R}_{3}}$

Simplemente sustituimos nuestros datos en la fórmula:

$\displaystyle {{R}_{T}}=3\Omega +6\Omega +8\Omega =17\Omega$

Fácil, muy fácil . . .!

Obtenemos una resistencia equivalente de 17Ω

Nota: Entre más resistencias se sumen de forma paralela, más pequeña se hace la resistencia equivalente, de forma contraria entre más resistencias se sumen en serie, mucho mayor será la resistencia equivalente

Resultados:

$\displaystyle {{R}_{T(paralelo)}}=1.6\Omega$

$\displaystyle {{R}_{T(serie)}}=17\Omega$

2 Comentarios Publicados

cukii dice:

11 abril, 2023 a las 12:26 pm

Excelente, me sirvió de mucho:D

Responder
1. María dice:
  
  2 junio, 2023 a las 8:48 am
  
  Gracias por esta ayuda me sirvió de mucho
  
  Responder

Deja una respuesta Cancelar la respuesta