Solución 3 Ejercicio Resuelto de Resistencias en Paralelo

Con este tercer problema de Resistencias en Paralelo, el alumno finalmente refuerza el uso de la fórmula utilizando los despejes de la fórmula, ir viendo las diversas variables que se pueden obtener a través de la fórmula de la ley del ohm y que resuelve todo tipo de problemas que se puede encontrar en algún examen o tarea. 😊👇

Nivel de Dificultad: ⭐⭐⭐

Problema 6.- Tres aparatos eléctricos de 8Ω, 15Ω y 20Ω, ,se conectan en paralelo a una batería de 45V, a) calcular la resistencia equivalente o total, b) determinar la corriente total suministrada por la batería, c) ¿cuál es la corriente que circula en cada aparato?

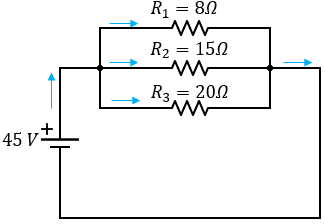
Resistencias en Paralelo problemas

Solución:

Este problema es más completo que los anteriores, en este ejemplo vemos que nos piden mezclar la ley del ohm para obtener ciertos valores como la corriente en cada aparato, o la corriente total. La solución es muy fácil, y la realizaremos paso a paso.

Obtener la resistencia total o equivalente
Obtener la corriente total en el circuito
Obtener la corriente en cada aparato

Datos:

$\displaystyle {{R}_{1}}=8\Omega$

$\displaystyle {{R}_{2}}=15\Omega$

$\displaystyle {{R}_{3}}=20\Omega$

$\displaystyle {{V}_{(Fuente)}}=45V$

a) Obtener la resistencia equivalente

Pasamos a sumar las resistencias en paralelo:

$\displaystyle {{R}_{T}}=\frac{1}{\frac{1}{8\Omega }+\frac{1}{15\Omega }+\frac{1}{20\Omega }}$

Qué también se puede escribir de esta forma:

$\displaystyle \frac{1}{{{R}_{T}}}=\frac{1}{8\Omega }+\frac{1}{15\Omega }+\frac{1}{20\Omega }$

Realizando la división:

$\displaystyle \frac{1}{{{R}_{T}}}=0.125\Omega +0.066\Omega +0.05\Omega$

Sumando

$\displaystyle \frac{1}{{{R}_{T}}}=0.242\Omega$

Que lo podemos escribir de la siguiente forma:

$\displaystyle {{R}_{T}}=\frac{1}{0.242\Omega }$

Dividiendo obtenemos la resistencia total

$\displaystyle {{R}_{T}}=4.14\Omega$

Por lo que la resistencia total o equivalente es de 4.14 Ω

b) Obtener la corriente total del circuito

Como ya sabemos a cuanto equivale la resistencia equivalente, es muy fácil poder encontrar la corriente total del circuito porque podemos aplicar la ley del ohm

$\displaystyle I=\frac{{{V}_{T}}}{R}$

Sustituyendo nuestros datos en la fórmula, obtenemos:

$\displaystyle I=\frac{V}{{{R}_{T}}}=\frac{45V}{4.15\Omega }=10.87A$

Es decir que en el circuito circulan 10.87 Amperes

c) Obtener la corriente que circula en cada aparato

Cuando la corriente llega al punto donde están las tres resistencias, estas corrientes se distribuyen en cada resistencia o en cada aparato, y se calcula de forma individual de la siguiente forma:

Calculando la corriente que pasa por el aparato 1

$\displaystyle {{I}_{1}}=\frac{V}{{{R}_{1}}}=\frac{45V}{8\Omega }=5.625A$