Solución Problema 1 de Ecuación de Continuidad

En este ejemplo de los problemas resueltos para ejercicios de práctica del tema de Ecuación de Continuidad, es importante tener en cuenta el uso correcto de la fórmula, es por eso que se realizan los ejercicios paso a paso con su solución correspondiente. Recuerde que con este tipo de ejemplos el alumno podrá corroborar su respuesta y verificar si ha llegado al mismo resultado. 😊👇

Nivel de Dificultad: ⭐⭐

Problema 3.- Por una tubería de 5.08 cm de diámetro circula agua a una velocidad cuya magnitud es de 1.6 m/s. Calcular la magnitud de la velocidad que llevará el agua al pasar por un estrechamiento de la tubería donde el diámetro es de 4 cm.

Ecuación de Continuidad problemas

Solución:

Los problemas de continuidad, son problemas relativamente fáciles de resolver. Pues al tener la mayor cantidad de variables como datos, entonces solo hace falta sustituir en la fórmula y encontrar el resultado, pero también debemos ser muy cuidadoso con las unidades. En este ejemplo vemos los datos del diámetro expresados en centímetros, para nuestro cálculo lo tendremos que usar en términos de metros, esto es por el SI "Sistema Internacional de Unidades", así qué comencemos a resolver el problema 😀

Obtener la magnitud de la velocidad del agua

Datos:

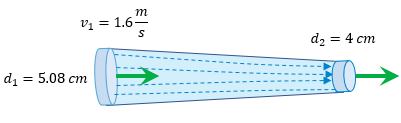
$\displaystyle {{d}_{1}}=5.08cm\left( \frac{1m}{100cm} \right)=0.0508m$

$\displaystyle {{d}_{2}}=4cm\left( \frac{1m}{100cm} \right)=0.04m$

$\displaystyle {{v}_{1}}=1.6\frac{m}{s}$

a) Obtener la magnitud de la velocidad del agua

Recordemos que la ecuación de continuidad, está expresada de la siguiente forma:

$\displaystyle {{A}_{1}}{{v}_{1}}={{A}_{2}}{{v}_{2}}$

El problema nos pide encontrar la velocidad final, es decir a "V2" , entonces despejamos:

$\displaystyle {{v}_{2}}=\frac{{{A}_{1}}{{v}_{1}}}{{{A}_{2}}}$

Antes de sustituir nuestros datos, debemos de encontrar primero las áreas de las secciones transversales. Así que aplicamos:

♦ Encontrando el área de las secciones

⭕ Área 1

$\displaystyle {{A}_{1}}=\frac{\pi {{d}_{1}}^{2}}{4}=\frac{\pi {{\left( 0.0508m \right)}^{2}}}{4}=0.0020{{m}^{2}}$

⭕ Área 2

$\displaystyle {{A}_{2}}=\frac{\pi {{d}_{2}}^{2}}{4}=\frac{\pi {{\left( 0.04m \right)}^{2}}}{4}=0.0012{{m}^{2}}$

Ahora si podemos sustituir en la fórmula, para encontrar la velocidad final:

$\displaystyle {{v}_{2}}=\frac{{{A}_{1}}{{v}_{1}}}{{{A}_{2}}}=\frac{\left( 0.0020{{m}^{2}} \right)\left( 1.6\frac{m}{s} \right)}{0.0012{{m}^{2}}}=2.66\frac{m}{s}$

Por lo que la magnitud de la velocidad del agua es de 2.66 m/s

Resultado:

$\displaystyle {{v}_{2}}=2.66\frac{m}{s}$

7 Comentarios Publicados

Heriberto Mendoza dice:

7 diciembre, 2022 a las 5:14 am

Muy bien la explicación

Responder
1. Carlos julián dice:
  
  7 diciembre, 2022 a las 7:50 pm
  
  Muchas gracias Heriberto!
  
  Responder
  1. Javier dice:
    
    19 febrero, 2024 a las 10:19 pm
    
    si tomo como area 1: 2.02x10-3
    Y area 2: 1.25x10-3, también es correcto? Al hacer la operacion del diametro en mi calculadora obtuve esos valores
    
    Responder
JOSE ANTONIO dice:

18 enero, 2023 a las 10:41 am

DE DONDE SALE EL 4 DE LAS AREAS ?

Responder
1. Carlos julián dice:
  
  29 enero, 2023 a las 9:08 am
  
  Es el área del círculo escrita en términos del diámetro, si fuera en radio es lo mismo. Haz la prueba!
  
  Responder
Carlos dice:

14 mayo, 2023 a las 9:29 pm

Muchas gracias tocallo , la verdad es que son de gran ayuda , super la explicacion ,me es mas facil entender.
saludos.

Responder
Isabel Sofia dice:

1 junio, 2023 a las 2:18 pm

De donde sale el 0.0020m^2

Responder

Deja una respuesta Cancelar la respuesta