Solución Problema 1 Ley de Cosenos

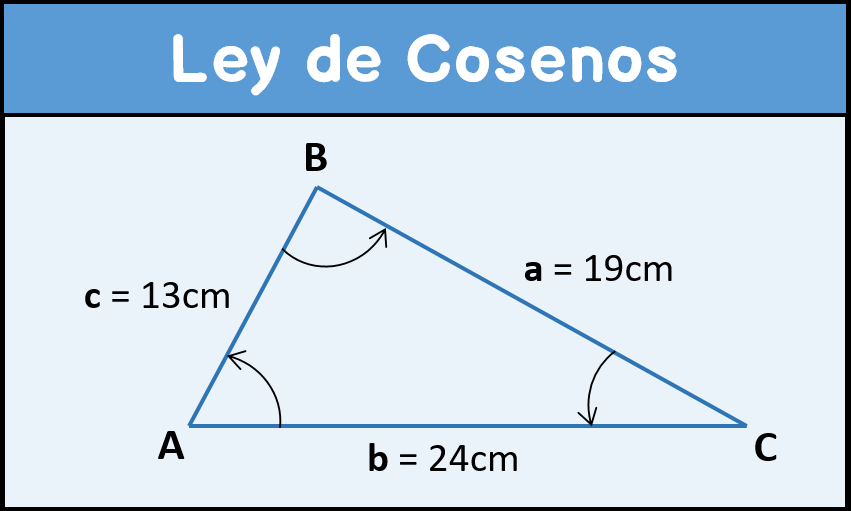
En el siguiente ejercicio resuelto se vuelve a plantear el problema, el triángulo y su solución.

Nivel de Dificultad: ⭐⭐

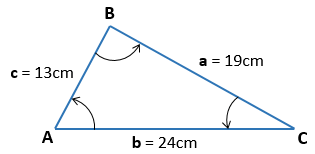
3.- Calcula los elementos de un triángulo oblicuángulo si se sabe que a = 19 cm, b = 24 cm y c = 13 cm.

Solución:

Lo primero que tenemos que hacer es recopilar nuestros datos, todo lo que el triángulo oblicuángulo nos ofrece de comienzo, para ello colocamos, los lados:

a = 19 cm.

b = 24 cm.

c = 13 cm.

Vamos a utilizar la fórmula general de la ley de cosenos, siempre y cuando hagamos los despejes correctos para llegar a las nuevas fórmulas que veremos a continuación:

$\displaystyle \cos A=\frac{{{b}^{2}}+{{c}^{2}}-{{a}^{2}}}{2bc}$

$\displaystyle \cos B=\frac{{{a}^{2}}+{{c}^{2}}-{{b}^{2}}}{2ac}$

$\displaystyle \cos C=\frac{{{a}^{2}}+{{b}^{2}}-{{c}^{2}}}{2ab}$

Para cada caso hemos despejado las fórmulas y con ello empezar a sustituir nuestros datos para obtener los valores faltantes de nuestro triángulo.

Para obtener el ángulo A

$\displaystyle \cos A=\frac{{{b}^{2}}+{{c}^{2}}-{{a}^{2}}}{2bc}=\frac{{{(24cm)}^{2}}+{{(13cm)}^{2}}-{{(19cm)}^{2}}}{2(24cm)(13cm)}$

$\displaystyle \cos A=\frac{{{(24cm)}^{2}}+{{(13cm)}^{2}}-{{(19cm)}^{2}}}{2(24cm)(13cm)}=\frac{384c{{m}^{2}}}{624c{{m}^{2}}}$

$\displaystyle \cos A=\frac{384c{{m}^{2}}}{624c{{m}^{2}}}=0.6153$

Despejando A

$\displaystyle A=\arccos (0.6153)=52.02{}^\circ$

Listo, ahora veamos como obtener el siguiente ángulo.

Para obtener el ángulo B

$\displaystyle \cos B=\frac{{{(19cm)}^{2}}+{{(13cm)}^{2}}-{{(24cm)}^{2}}}{2(19cm)(13cm)}=\frac{-46c{{m}^{2}}}{494c{{m}^{2}}}=-0.0931$

Despejando B

$\displaystyle B=\arccos (-0.0931)=95.34{}^\circ$

Para obtener el ángulo C

$\displaystyle \cos C=\frac{{{(19cm)}^{2}}+{{(24cm)}^{2}}-{{(13cm)}^{2}}}{2(19cm)(24cm)}=\frac{768c{{m}^{2}}}{912c{{m}^{2}}}=0.8421$

Despejando C

$\displaystyle C=\arccos (0.8421)=32.64{}^\circ$

Resultados

$\displaystyle \begin{array}{l}\sphericalangle A=52.02{}^\circ \\\sphericalangle B=95.34{}^\circ \\\sphericalangle C=32.64{}^\circ \end{array}$

Comprobación:

$\displaystyle \sphericalangle A+\sphericalangle B+\sphericalangle C=52.02{}^\circ +95.34{}^\circ +32.64{}^\circ =180{}^\circ$

Problema Resuelto 😎

Esperamos que este ejercicio te haya dado de la misma manera, en caso de dudas favor de realizar las preguntas correspondientes en el artículo de la Ley de Cosenos

2 Comentarios Publicados

Valak dice:

9 noviembre, 2023 a las 11:49 am

Son los mejores, muchas gracias

Responder
1. Carlos julián dice:
  
  11 noviembre, 2023 a las 10:30 am
  
  Gracias a ti !!!
  
  Responder

Deja una respuesta Cancelar la respuesta