Solución Problema 1 - Parábola Fuera del Origen
En el ejercicio se plantea el siguiente problema. Leerse con mucho cuidado
Nivel de Dificultad: 
Problema 3.- Hallar la ecuación de la parábola cuyo vértice es el punto (3, 4) y cuyo foco es el punto (3, 2). Hallar también la ecuación de su directriz y la longitud de su lado recto.
Solución:
Para darle solución a este problema, es importante graficar al menos el punto del vértice y el punto del foco, serán indispensable para la solución del ejercicio.
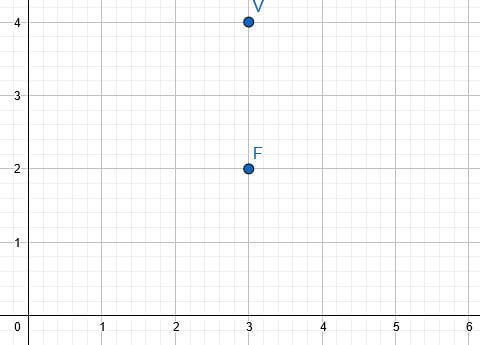
Después podemos darnos cuenta que el vértice V y el foco F de una parábola están sobre su eje, es decir sobre el eje de las "y" y pasa precisamente en x = 3, por lo que podemos decir que dicho eje es paralelo al eje "Y", tal como vemos en la imagen. La ecuación de la parábola asume la forma:
Como el vértice V es el punto (3, 4), donde h = 3 y k = 4
Entonces podemos decir que:
Ahora bien, podemos observar que el valor de P se puede encontrar restando la distancia que existe entre el vértice y el foco de forma vertical, es decir (4 - 2 ) y esto nos da el valor de 2, Pero como el foco F está abajo del vértice V, la parábola se abre hacia abajo y p es negativo. Por tanto, p = -2 , y la ecuación de la parábola es:
Por tanto la longitud del lado recto es 8.
La ecuación de la directriz:
La directriz tiene que sumar dos unidades también hacía arriba en dirección del vértice, por lo tanto al sumar 4 +2 = 6
Eso quiere decir que Y = 6
Que es nuestra solución.
Muy bueno tu respuesta gracias